Задание 4

Разработать логическую схему КЦУ, функционирование которого задано таблицей истинности (таблица 7).

1. Записать СДНФ и СКНФ.

2. Построить логическую схему устройства в базисе И, ИЛИ, НЕ.

3. Записать СДНФ через логическую операцию И-НЕ.

4. Построить логическую схему устройства в базисе И-НЕ.

5. Записать СКНФ через логическую операцию ИЛИ-НЕ.

6. Построить логическую схему устройства в базисе ИЛИ-НЕ.

7. Проверить правильность функционирования логических схем КЦУ для пятого набора аргументов.

8. Выполнить расчет затрат оборудования по Квайну, сделать вывод.

Таблица 7 – Исходные данные к заданию 4

Номер набора аргументов	Наборы аргументов			Номер варианта
				0	1	2	3	4	5	6	7	8	9
	х3	х2	х1
0	0	0	0	1	0	1	1	1	0	1	1	0	1
1	0	0	1	0	1	1	0	1	1	0	0	0	0
2	0	1	0	1	1	0	1	1	0	0	0	0	1
3	0	1	1	1	1	0	1	0	0	0	0	1	0
4	1	0	0	1	0	0	1	0	0	1	1	1	0
5	1	0	1	0	1	1	0	0	1	1	0	1	0
6	1	1	0	1	0	1	0	1	0	0	1	0	1
7	1	1	1	0	1	1	1	1	1	0	0	1	1

Методические указания по выполнению задания 4

Все схемы цифровых устройств построены на элементах, выполняющих логические операции. Такие элементы принято называть логическими элементами (ЛЭ). При конкретной физической реализации логических состояний используются элементы, для которых характерны два устойчивых состояния. Например, электрическое реле – замкнуто, разомкнуто; элемент индикации – светится, не светится и т.д.

В логике не требуется знания абсолютного значения величины, поэтому физическая величина, подвергаемая логическим преобразованиям, называется переменной, или аргументом, и представляется как более положительная (Н) или менее положительная (L). Этим двум значениям, называемым логическими уровнями, условно присваиваются значения лог. 1 и лог. 0, или, наоборот, в зависимости от принятого соглашения.

Логические переменные могут подвергаться различным преобразованиям с использованием логических элементов (ЛЭ). Такие преобразования описываются с помощью переключательных (логических) функций. Функция от входных переменных называется переключательной (логической), если она так же, как ее аргументы, принимает два значения: лог. 1 или лог. 0. На рисунке 13 представлен условный логический элемент, реализующий определенную функцию в зависимости от значений входных переменных.

Рисунок 13 – Условное графическое обозначение (УГО) ЛЭ

Любая логическая функция (ЛФ) может быть задана двумя способами: в виде формул и в виде таблиц истинности (ТИ). В ТИ приводятся значения ЛФ в зависимости от сочетания переменных.

При этом для того чтобы задать переключательную функцию, не обязательно задавать все ее значения при всех сочетаниях переменных, а достаточно знать состояния, при которых она, например, равна лог. 1, так как для всех остальных состояний переменных значение ЛФ равно лог. 0.

В формульном виде функция в своей основе имеет набор логических произведений (или сумм) переменных, связанных между собой, как правило, знаками логических сумм (или произведений).

Произведение переменных, в которое каждая из переменных входит только один раз в прямом или инверсном виде, называется минтермом (т).

Сумма переменных, в которую каждая из переменных входит только один раз в прямом или инверсном виде, называется макстермом (М).

Так, например, у двух переменных может бытьчетыре возможных макстерма или минтерма, виды которых представлены в таблице 4.

Таблица 8 – Макстеры и минтермы двух переменных

Переменные		Макстермы	Минтермы
х2	х1	М	т
0	0
0	1
1	0
1	1

Количество переменных, входящих в макстерм или минтерм, называется рангом. В рассматриваемом примере ранг равен 2.

Рассмотрим правила перехода от табличной формы записи ЛФ к формульной. Например, функция задана в виде таблицы истинности (таблица 9).

Таблица 9 – Таблица истинности ЛФ

М	х3	х2	х1	f	т
	0	0	0	1
	0	0	1	1
	0	1	0	0
	0	1	1	1
	1	0	0	0
	1	0	1	0
	1	1	0	1
	1	1	1	1

Для перехода от табличной формы к формульной следует руководствоваться следующими положениями.

1. Если функция алгебры логики задана таблицей истинности, то из таблицы всегда можно взять логическую сумму – дизъюнкцию всех переменных, для которых ЛФ равна единице. Эта запись будет точно представлять функцию и называться совершенной дизъюнктивной нормальной формой (СДНФ) представления функции. СДНФ – это логическая сумма минтермов, при которых значение функции равно единице:

. (1)

2. Если функция алгебры логики задана таблицей истинности, то из таблицы всегда можно взять логическое произведение – конъюнкцию всех переменных, для которых ЛФ равна нулю. Эта запись будет точно представлять функцию и называться совершенной конъюнктивной нормальной формой (СКНФ) представления функции. СКНФ – это логическое произведение макстермов, при которых значение функции равно нулю:

. (2)

Одна из основных задач синтеза ЦУ заключается в выборе типов элементов, на которых будут реализовываться заданные функции. Поэтому необходимо определить минимальный набор логических элементов (базис), образующих функционально полную систему элементов.

Базис – это функционально полный набор элементов, с помощью которого можно реализовать сколь угодно сложную переключательную функцию. Их может быть несколько. Базис из логических элементов И, ИЛИ, НЕ (рисунок 14) называют основным.

Рисунок 14 – Условное графическое обозначение ЛЭ И, ИЛИ, НЕ

Также функционально полную систему образуют логический элемент И-НЕ или ИЛИ-НЕ (рисунок15).

Рисунок 15 – Условное графическое обозначение ЛЭ И-НЕ, ИЛИ-НЕ

В таблице 10 представлены отечественные и зарубежные аналоги условных графических обозначений основных логических элементов, которые реализуют ЛФ двух аргументов.

Таблица 10 – Зарубежные аналоги УГО ЛЭ

Логическая функция	Отечественное УГО	Зарубежное УГО
НЕ
И
ИЛИ
И-НЕ
ИЛИ-НЕ

Требования к построению схем цифровых устройств изложены в соответствующих стандартах. Схема цифрового устройства представляет собой совокупность условных графических обозначений микросхем, на которых реализовано это устройство, и связей между ними.

Построим логическую схему устройства по выражению (1). Для этого потребуется:

1. пять логических элементов 2 И;

2. один логический элемент 5 ИЛИ;

3. три логических элемента НЕ.

Логическая схема устройства в базисе И, ИЛИ, НЕ, построенная по логической функции (1), представлена на рисунке 16.

Рисунок 16 – Логическая схема устройства в базисе И, ИЛИ, НЕ

Проверим правильность функционирования логической схемы КЦУ. Для этого проставим на выходах всех логических элементов значения сигналов для пятого набора аргументов, полученный на выходе сигнал сравним со значением функции в таблице истинности.

Построим логическую схему устройства по выражению (2). Для этого потребуется:

1. два логических элемента 2 И;

2. один логический элемент 3 ИЛИ;

3. три логических элемента НЕ.

Логическая схема устройства в базисе И, ИЛИ, НЕ, построенная по логической функции (2), представлена на рисунке 17.

Рисунок 17 – Логическая схема устройства в базисе И, ИЛИ, НЕ

Проверим правильность функционирования логической схемы КЦУ. Для этого проставим на выходах всех логических элементов значения сигналов для пятого набора аргументов, полученный на выходе сигнал сравним со значением функции в таблице истинности.

Рассмотрим пример синтеза КЦУ в базисе И-НЕ для той же ЛФ.

Преобразуем ЛФ (1) в базис И-НЕ, используя правило де Моргана и закон двойного отрицания:

=

Построим логическую схему устройства в базисе И-НЕ по выражению (1), при этом одиночные отрицания аргументов реализуем на основе ЛЭ 2 И-НЕ с объединенными входами. Для этого необходимо использовать:

1. три логических элемента 2 И-НЕ;

2. пять логических элементов 3 И-НЕ.

3. один логический элемент 5 И-НЕ.

Логическая схема устройства в базисе И-НЕ представлена на рисунке 18.

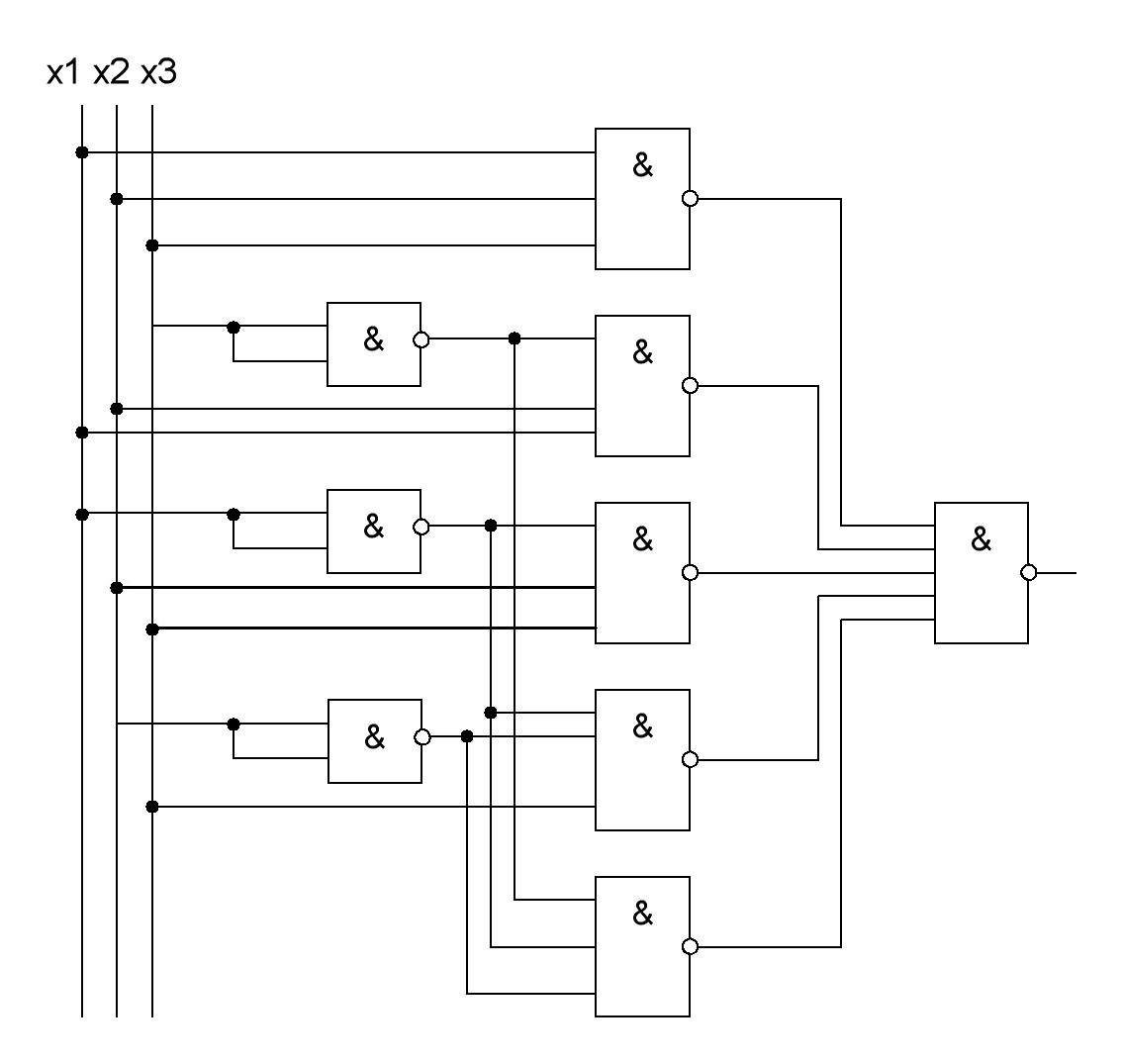
Рисунок 18 – Логическая схема устройства в базисе И-НЕ

Проверим правильность функционирования логической схемы КЦУ. Для этого проставим на выходах всех логических элементов значения сигналов для пятого набора аргументов, полученный на выходе сигнал сравним со значением функции в таблице истинности.

Преобразуем ЛФ (2) в базис ИЛИ-НЕ, используя правило де Моргана и закон двойного отрицания:

.

Построим логическую схему устройства в базисе ИЛИ-НЕ по выражению (2), при этом одиночные отрицания аргументов реализуем на основе ЛЭ 2 ИЛИ-НЕ с объединенными входами. Для этого необходимо использовать:

1. три логических элемента 2 ИЛИ-НЕ;

2. четыре логических элемента 3 ИЛИ-НЕ.

Логическая схема устройства в базисе ИЛИ-НЕ представлена на рисунке 19.

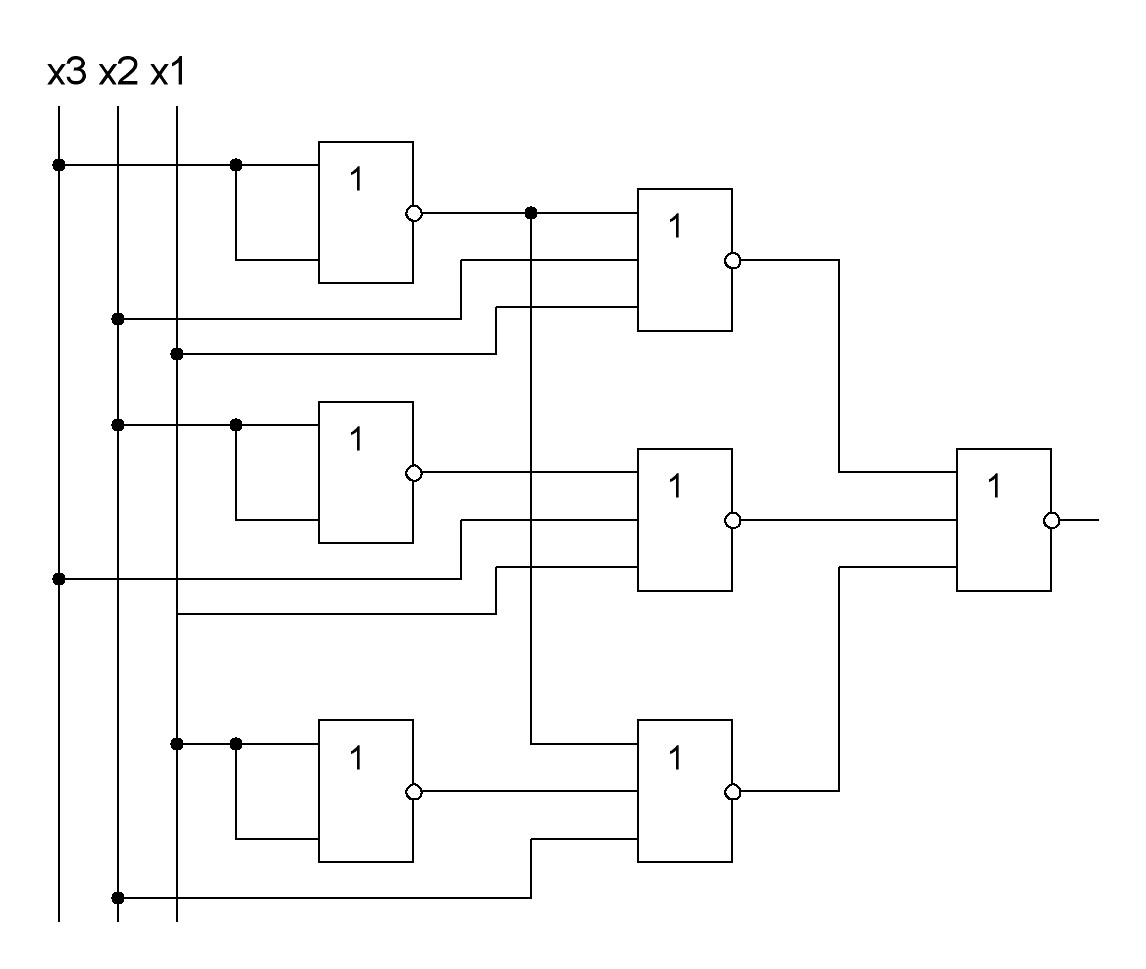
Рисунок 19 – Логическая схема устройства в базисе ИЛИ-НЕ

Проверим правильность функционирования логической схемы КЦУ.

Для этого проставим на выходах всех логических элементов значения сигналов для пятого набора аргументов, полученный на выходе сигнал сравним со значением функции в таблице истинности.

Выполним расчет затрат оборудования по Квайну (С) для логических схем КЦУ (рисунки 16-19).

Так как количество входов у всех логических элементов КЦУ является объективной мерой для оценки сложности КЦУ и каждому входу ЛЭ соответствует технический компонент (условный транзистор), то затраты оборудования по Квайну для схем соответственно равны:

С=5х2+1х5+3х1=18 (усл. транзисторов);

С=2х2+1х3+3х1=10 (усл. транзисторов);

С=3х2+5х3+1х5=26 (усл. транзисторов);

С=3х2+4х3=18 (усл. транзисторов).

По полученным результатам можно сделать вывод, что схема, построенная по СКНФ в основном базисе, является более экономичной. При этом следует помнить, что данная оценка объективна, доступна разработчику на самых ранних этапах проектирования, но при этом не является абсолютной, и поэтому при синтезе КЦУ используется ряд других критериев.