
- •1 Моделі однолінійних систем масового обслуговування
- •1.1 Основні поняття і визначення. Дисципліна обслуговування.
- •1.2 Марківські процеси і ланцюги та їх властивості
- •1.2.1 Поняття марківського процесу і ланцюга
- •1.2.2 Дискретний ланцюг Маркова
- •2. Математична модель процесів народження і загибелі
- •2.1 Рівняння Колмогорова-Чепмена та рівняння Колмогорова
- •2.2 Ергодичні ймовірності процесів народження і загибелі
- •3 Математична модель системи мо з кінцевим числом станів
- •3.1 Зворотні та прямі рівняння Колмогорова
- •3.2 Математичні моделі консервативних систем мо
- •3.3 Обчислення інтенсивностей переходів марківських процесів
- •3.4 Система із n приладів і r із них можуть відновлюватись
- •2. Які величини є елементами інфінітезимальної матриці?
- •4 Моделі багатолінійних систем масового обслуговування
- •4.1 Основні типи систем масового обслуговування
- •4.2 Символіка систем мо
- •4.2 Математичні моделі основних типів систем мо
- •4.3 Багатолінійна система м/м/n/n з обмеженою чергою і обмеженим часом очікування
- •4.4 Обчислення ергодичних розподілів системи мо типу m/m/n/n
- •4.4.1 Багатоканальна система з обмеженою чергою (m/m/n/n)
- •4.4.2 Багатоканальна система з нескінченою чергою і обмеженим часом очікування (m/m/n)
- •4.4.3 Система мо з очікуванням і необмеженою чергою (m/m/n; )
- •5 Оптимальні потоки у мережах
- •5.1 Поняття про мережу і основні визначення
- •5.2 Задача про максимальний потік у мережі
- •5.3 Теореми про оптимальні потоки у мережах
- •5.4 Метод розстановки поміток для знаходження максимального потоку
- •5.5 Модифікований метод розстановки поміток для знаходження максимального потоку
- •5.6 Алгоритм Форда-Фалкерсона знаходження максимального потоку
- •6 Багатополюсні максимальні потоки
- •6.1 Умова реалізації
- •6.2 Аналіз мережі
- •7 Найкоротші ланцюги і потоки мінімальної вартості
- •7.1 Найкоротші ланцюги
- •7.2 Багатополюсні найкоротші ланцюги
- •7.3 Багатополюсні ланцюги максимальної пропускної здатності
- •7.4 Потоки мінімальної вартості
4.2 Символіка систем мо
Для короткої характеристики систем МО застосовують символіку, яка викладена нижче.
Система МО характеризується 4-ма величинами А/В/S/m, де
![]() – кількість
обслуговуючих приладів;
– кількість
обслуговуючих приладів;
![]() – ємність
накопичувача;
– ємність
накопичувача;
А – потік вимог:
А = GI (general independent ) – рекурентний потік вимог;
А = M (Markov ) – пуасоновський потік вимог;
А = Еk (Erlang ) – рекурентний потік вимог з розподілом Ерланга порядку k;
А = D (deterministic) – потік з постійними інтервалами між вимогами;
В – характеризує випадкові послідовності тривалостей обслуговування на окремих приладах:
В = G – послідовність незалежних однаково розподілених тривалостей обслуговування на кожному приладі;
В = М – послідовність незалежних, експоненціально-розподілених тривалостей на кожному приладі.
4.2 Математичні моделі основних типів систем мо
Системи МО типу M/M/1 і M/M/1/N, розглянуті нами раніше (див. приклади 2.1 і 2.2). Зараз ми розглянемо інші типи систем МО.
4.2.1 Система з втратами. Система типу M/M/N/0 складається із однакових приладів, які обслуговують вимоги за експоненціальним законам з параметром . Вхідний потік також має експоненціальне розподілення з параметром . Якщо в момент поступлення вимоги всі прилади зайняті, то вимога губиться.
Якщо
![]() -
число вимог в системі МО в момент часу
,
що співпадають з числом занятих приладів,
то
-
процес розмноження і загибелі з
параметрами
-
число вимог в системі МО в момент часу
,
що співпадають з числом занятих приладів,
то
-
процес розмноження і загибелі з
параметрами
![]() Тому у відповідності з формулою (2.7)
Тому у відповідності з формулою (2.7)
 ,
,
де
![]() .
.
Оскільки
![]() і
і
![]() ,
то
,
то
![]() ,
,
де
 .
.
Розглянемо частковий випадок, коли система МО має один обслуговуючий прилад. Для системи типу M/M/1/0, матимемо
![]()
і відповідно
![]() .
.
Таким чином, в
стаціонарному стані система МО
характеризується двома ймовірностями
![]() і
і
![]() ;
- ймовірність того, що прилад вільний
від обслуговування і
- ймовірність того, що прилад зайнятий
обслуговуванням. Граф системи МО
показаний на рис.6.4.
;
- ймовірність того, що прилад вільний
від обслуговування і
- ймовірність того, що прилад зайнятий
обслуговуванням. Граф системи МО
показаний на рис.6.4.
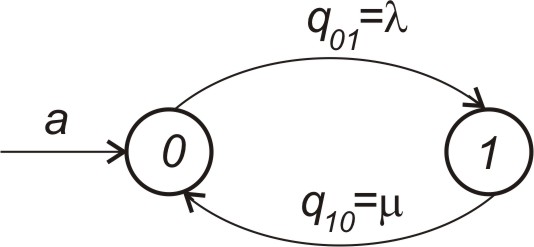
Рисунок 4.6 – Граф системи МО типу М/М/1/0.
Знайдемо ймовірності
і
як функції часу
.
Для цього запишемо рівняння (3.14) для
![]() .
Маємо
.
Маємо
![]()
з початковою умовою
![]() і
і
![]() .
Це означає, що прилад в момент часу
.
Це означає, що прилад в момент часу
![]() вільний від обслуговування.
вільний від обслуговування.
У відповідності з формулою (3.13) обчислимо
![]() .
.
Отже,

Розв'язок отриманої системи рівнянь здійснимо шляхом використання перетворення Лапласа. Маємо
![]() ;
;
![]() .
.
Отриману систему рівнянь запишемо в такому вигляді:

Звідси знаходимо
![]()
![]()
Знайдемо полюси
функцій
![]() і
і
![]() ,
розв'язавши рівняння (
,
розв'язавши рівняння (![]() ).
Отримуємо
).
Отримуємо
![]() і
і
![]() .Використовуючи
формулу
.Використовуючи
формулу
![]() ,
,
Знаходимо (N=1)
![]() ,
,
![]() .
.
Значення величин
![]() і
і
![]() в стаціонарному стані знайдемо, якщо
t
буде прямувати до нескінченності. Тоді
в стаціонарному стані знайдемо, якщо
t
буде прямувати до нескінченності. Тоді
![]() і
і
![]()
Отриманий результат, природно, співпадає із результатом, який отриманий на основі формули (2.7).
4.3 Багатолінійна система м/м/n/n з обмеженою чергою і обмеженим часом очікування
Нехай багатолінійна
система МО має
приладів
і буфер ємністю
.Це
означає, що в будь-який момент часу
в системі можуть одночасно обслуговуватись
не більше
вимог і не більше
заявок знаходяться в черзі. Отже, в
системі МО одночасно може знаходитись
не більше ніж
![]() заявок.
Допустимо, що на вхід системи наступає
потік вимог з експоненціальним законом
розподілу, параметр якого
.
Обслуговування заявок, які наступають
в систему МО, здійснюються у відповідності
з принципом FCFS.
Будемо вважати, що тривалість перебування
в черзі випадкова незалежна від інших
факторів величина, яка має експоненціальний
закон розподілу з параметром
заявок.
Допустимо, що на вхід системи наступає
потік вимог з експоненціальним законом
розподілу, параметр якого
.
Обслуговування заявок, які наступають
в систему МО, здійснюються у відповідності
з принципом FCFS.
Будемо вважати, що тривалість перебування
в черзі випадкова незалежна від інших
факторів величина, яка має експоненціальний
закон розподілу з параметром
![]() .
.
Отже, процес
функціонування системи МО можна описати
наступним чином. Вимога що наступає в
систему МО, може бути негайно прийнята
до обслуговування, якщо в системі є
вільний прилад. Якщо вільних приладів
(каналів) в системі немає, то при наявності
вільних місць в буфері вимога стає в
чергу. Із черги така вимога може попасти
на обслуговування або покинути систему,
якщо час очікування перевершить деяку
величину
![]() .
В такому випадку вимога вважається
загубленою. Загубленими вважається і
вимоги, які застали буфер заповненим.
.
В такому випадку вимога вважається
загубленою. Загубленими вважається і
вимоги, які застали буфер заповненим.
Схематично описана
система МО зображена на рис. 4.7. До відомих
вже елементів системи тут долучений
потік
![]() ,
загублений із-за обмеженого часу
очікування.
,
загублений із-за обмеженого часу
очікування.
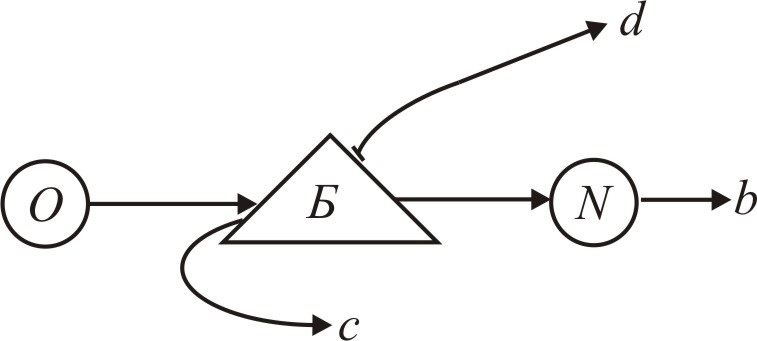
Рисунок 4.7 - Система МО типу М/М/N/n з обмеженим часом очікування
Стан системи МО
повністю визначається випадковим
процесом
- числом вимог в момент часу t.
Множина можливих станів системи
![]() .
.
Визначимо операції,
які відповідають стану
![]() .
При
.
При
![]() продовжується одна фіктивна операція
очікування вимоги
продовжується одна фіктивна операція
очікування вимоги![]() та і
операцій
та і
операцій
![]() обслуговування. Так як величина роботи,
що пов’язана з виконанням операцій,
виражена в одиницях часу, то
обслуговування. Так як величина роботи,
що пов’язана з виконанням операцій,
виражена в одиницях часу, то
![]() при
при
![]() .
При
інтенсивності виконання операцій
.
При
інтенсивності виконання операцій
![]() наступні
наступні
![]() (4.1)
(4.1)
Після закінчення
операції
![]() з ймовірністю 1 здійснюється перехід в
стан
з ймовірністю 1 здійснюється перехід в
стан
![]() (в систему поступила нова вимога і
кількість вимог збільшилася на 1).
(в систему поступила нова вимога і
кількість вимог збільшилася на 1).
Закінчення однієї
із операцій
![]() приводить до обслуговування однієї
вимоги, що означає перехід системи в
стан
приводить до обслуговування однієї
вимоги, що означає перехід системи в
стан
![]() .Тому:
.Тому:
![]() (4.2)
(4.2)
Якщо
![]() і
і
![]() ,
то має місце одна фіктивна операція
очікування
вимоги, N
операцій обслуговування
,
то має місце одна фіктивна операція
очікування
вимоги, N
операцій обслуговування
![]() і
і
![]() фіктивних операцій очікування втрати
вимоги.
фіктивних операцій очікування втрати
вимоги.
Отже,
 (4.3)
(4.3)
Підставляючи
рівності (4.1) і (4.2) в (3.18) визначимо
інтенсивності переходів
![]() для
для
![]() (операція очікування)
(операція очікування)
![]() ;
(4.4)
;
(4.4)
для значень
![]() (операція обслуговування)
(операція обслуговування)
![]() .
(4.5)
.
(4.5)
Отже,
![]() (4.6)
(4.6)
Тепер обчислимо
за формулою(3.18) інтенсивності переходів
марківського процесу
для випадку коли
![]() .
Для цього підставимо(4.2) і (4.3) в
формулу(3.18). В результаті отримаємо:
.
Для цього підставимо(4.2) і (4.3) в
формулу(3.18). В результаті отримаємо:
![]() .
.
Отже,
![]() (4.7)
(4.7)
Наведені обчислення дають змогу зробити висновок, що інтенсивності переходів визначаються такими співвідношеннями:
![]() ,
,
![]() (4.8)
(4.8)
І, на кінець, при
![]() не здійснюється операція очікування (
немає місця в буфері і вимога негайно
покидає систему МО).
не здійснюється операція очікування (
немає місця в буфері і вимога негайно
покидає систему МО).
![]()
Таким чином, математична модель системи МО типу M/M/N/n з обмеженою чергою і обмеженим часом очікування описується системою рівнянь (3,14) , в якій
![]() ;
;
![]() ;
;
![]() і
і
![]() для інших значень k
та j.
Крім того
для інших значень k
та j.
Крім того
![]() .
.
Значення
![]() для j
для j![]() [0,N+n]
обчислюються за допомогою формули
(4.8).
[0,N+n]
обчислюються за допомогою формули
(4.8).
Систему рівнянь (3.14) запишемо в розгорнутому вигляді, враховуючи, що індекс j приймає значення від 0 до N+n. Отже,
![]() ,
,
![]() ,
,
![]()
.......................................................................................
![]()
![]()
![]()
![]()
………………………………………………………….
![]()
![]() (4.9)
(4.9)
Обчислимо значення інтенсивностей переходів, які входять в систему рівнянь(4.9) . Обчислення виконаємо для значень j [0,N+n] . У відповідності з умовами(4.8) будемо мати для :
![]()
![]()
![]() ;
;
![]()
![]() ;
;
……………….....................................
![]()
![]() ;
;
![]()
![]()
![]()
![]() ;
;
![]()
![]() ;
;
![]()
...........................................................................................
![]()
![]()
![]()
![]()
для інших значень k та j .
З врахуванням інтенсивності переходів система рівнянь (4.9) набуде такого вигляду:
![]()
![]()
![]()
...................................................
![]()
![]()
![]()
![]()
...................................................................................
![]()
![]() (4.10)
(4.10)
Узагальнюючи отримані результати, можемо записати, що
![]() ,
,
для
значень
![]()
![]() ;
;
для
значень
![]()
![]() ;
;
![]()
Система рівнянь(4.10) повинна бути розв’язана з початковими умовами
![]()
![]() (4.11)
(4.11)
які характеризують систему МО в момент часу t=0. При цьому повинні виконуватись умови нормування:
![]() (4.12)
(4.12)
