
- •1 Моделі однолінійних систем масового обслуговування
- •1.1 Основні поняття і визначення. Дисципліна обслуговування.
- •1.2 Марківські процеси і ланцюги та їх властивості
- •1.2.1 Поняття марківського процесу і ланцюга
- •1.2.2 Дискретний ланцюг Маркова
- •2. Математична модель процесів народження і загибелі
- •2.1 Рівняння Колмогорова-Чепмена та рівняння Колмогорова
- •2.2 Ергодичні ймовірності процесів народження і загибелі
- •3 Математична модель системи мо з кінцевим числом станів
- •3.1 Зворотні та прямі рівняння Колмогорова
- •3.2 Математичні моделі консервативних систем мо
- •3.3 Обчислення інтенсивностей переходів марківських процесів
- •3.4 Система із n приладів і r із них можуть відновлюватись
- •2. Які величини є елементами інфінітезимальної матриці?
- •4 Моделі багатолінійних систем масового обслуговування
- •4.1 Основні типи систем масового обслуговування
- •4.2 Символіка систем мо
- •4.2 Математичні моделі основних типів систем мо
- •4.3 Багатолінійна система м/м/n/n з обмеженою чергою і обмеженим часом очікування
- •4.4 Обчислення ергодичних розподілів системи мо типу m/m/n/n
- •4.4.1 Багатоканальна система з обмеженою чергою (m/m/n/n)
- •4.4.2 Багатоканальна система з нескінченою чергою і обмеженим часом очікування (m/m/n)
- •4.4.3 Система мо з очікуванням і необмеженою чергою (m/m/n; )
- •5 Оптимальні потоки у мережах
- •5.1 Поняття про мережу і основні визначення
- •5.2 Задача про максимальний потік у мережі
- •5.3 Теореми про оптимальні потоки у мережах
- •5.4 Метод розстановки поміток для знаходження максимального потоку
- •5.5 Модифікований метод розстановки поміток для знаходження максимального потоку
- •5.6 Алгоритм Форда-Фалкерсона знаходження максимального потоку
- •6 Багатополюсні максимальні потоки
- •6.1 Умова реалізації
- •6.2 Аналіз мережі
- •7 Найкоротші ланцюги і потоки мінімальної вартості
- •7.1 Найкоротші ланцюги
- •7.2 Багатополюсні найкоротші ланцюги
- •7.3 Багатополюсні ланцюги максимальної пропускної здатності
- •7.4 Потоки мінімальної вартості
2. Які величини є елементами інфінітезимальної матриці?
3. Дайте визначення консервативної системи масового обслуговування.
4. Відносно яких змінних записана математична модель системи масового обслуговування з кінцевим числом станів?
3. Для системи масового обслуговування з кінцевим числом станів , інтенсивністю вхідного потоку =0,3 і інтенсивністю обслуговування =0,4 записати інфінітезимальну матрицю.
6. Для системи
масового обслуговування з кінцевим
числом станів
![]() ,
інтенсивністю вхідного потоку
=1,35
і інтенсивністю обслуговування
=1,4
визначити зміну перехідних ймовірностей
в часі.
,
інтенсивністю вхідного потоку
=1,35
і інтенсивністю обслуговування
=1,4
визначити зміну перехідних ймовірностей
в часі.
7. Задана інфінітезимальна матриця консервативної системи масового обслуговування
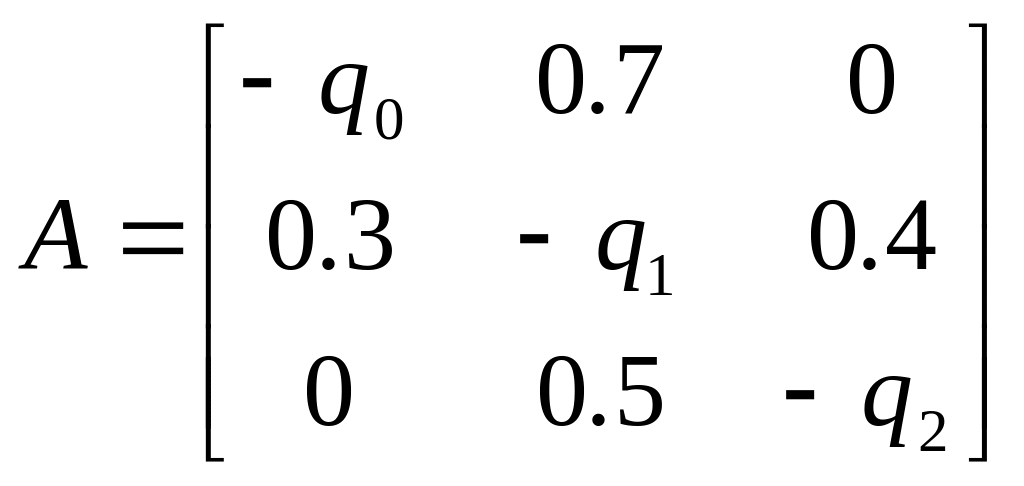 .
.
Чому дорівнюють
інтенсивності
![]() ,
,![]() ,
,
![]() ?
?
8. Для консервативної системи масового обслуговування, граф якої показаний на рисунку,
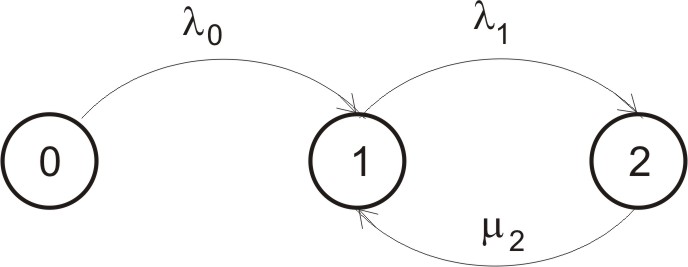
знайдіть її
розв’язок, який описує функціонування
такої системи, якщо
![]() ,
і
,
і
![]() ;
=1,6,
=1,63.
;
=1,6,
=1,63.
9. Для консервативної системи масового обслуговування, граф якої показаний на рисунку,
визначити ймовірність
знаходження системи в стані
![]() при нескінченно довгій її роботі, якщо
,
і
;
=0,12,
=0,14.
при нескінченно довгій її роботі, якщо
,
і
;
=0,12,
=0,14.
10. Система складається
із N
приладів, час безвідмовної роботи,
кожного із них експоненціально-розподілена
випадкова величина з параметром .
Число елементів, що знаходяться в момент
часу
в неробочому стані Хt=0,1,...,n.
Є r
n операторів,
кожен із яких може одночасно відновлювати
лише один прилад. Якщо число приладів,
що відмовили більше r,
то r елементів
відновлюються, інші утворюють чергу на
відновлення. Знайдіть інтенсивність
переходу системи
![]() із
стану
із
стану
![]() в
стан
в
стан
![]() при
при
![]() ,
,
![]() ,
,
![]() .
.
4 Моделі багатолінійних систем масового обслуговування
4.1 Основні типи систем масового обслуговування
Існують наступні типи систем МО.
Системи з втратами (рис. 4.1) – вимоги, які при поступленні не знаходить ні одного вільного приладу, губляться
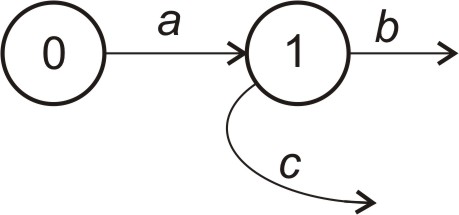
0 – джерела вимог;
1 – прилад.
Рисунок 4.1 – Система МО з втратами
Система з очікуванням (рис. 4.2) – можливе очікування для будь-якого числа вимог (або обмеженого числа вимог), які не можуть бути обслужені зразу. Вони складають чергу у відповідності з дисципліною обслуговування.
![]()
0 – джерело повідомлень;
1 – накопичувач;
2 – прилад.
Рисунок 4.2 – Система МО з очікуванням
Системи з обмеженим
накопичувачем (рис.4.3).
В системі в будь-який час може знаходитися
не більше ніж
вимог, де
![]() .
Отже, ємність накопичувача дорівнює
.
Отже, ємність накопичувача дорівнює
![]() (одна вимога обслуговується). Якщо в
момент поступлення вимоги в накопичувачі
вже є
інших вимог, то ці вимоги губляться
(покидають систему) (рис. 4.3)
(одна вимога обслуговується). Якщо в
момент поступлення вимоги в накопичувачі
вже є
інших вимог, то ці вимоги губляться
(покидають систему) (рис. 4.3)
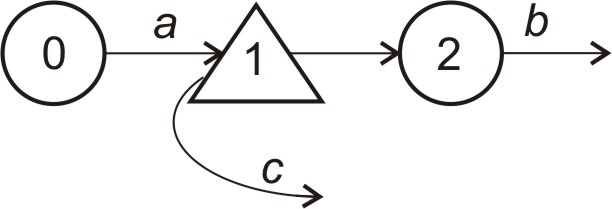 +
+
0 – джерело повідомлень;
1 – накопичувач;
2 – прилад.
Рисунок 4.3 – Система МО з обмеженим накопичувачем
Багатолінійна система із загальним накопичувачем (рис. 4.4). Допускається, що є приладів (ліній), кожний (кожна) із яких може одночасно обслуговувати одну вимогу. Якщо на деякому приладі закінчуються операція обслуговування і в накопичувачі є вимога, то вона негайно приймається до обслуговування.
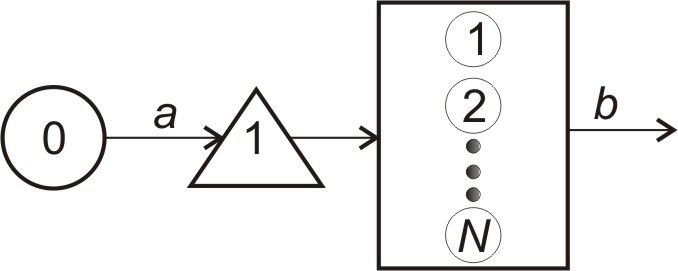
Рисунок 4.4 – Багатолінійна система МО із загальним накопичувачем
Невизначеність виникає в ситуації коли в момент поступлення вимоги вільні хоча б два прилади. В даному випадку допускають, що кожен із приладів вибирається з однаковою ймовірністю.
Система з обмеженим часом очікування (рис. 4.5). Вимоги, які поступають в систему (накопичувач) можуть очікувати початку обслуговування тільки обмежений час , де - випадкова величина.
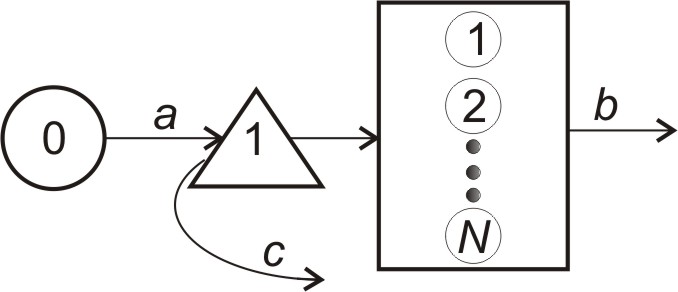
Рисунок 4.5 – Багатолінійна система МО з обмеженим часом очікування
Кількість заявок
в накопичувачі, очевидно дорівнює
![]() ,
де
– загальне число повідомлень в момент
часу
;
– це кількість приладів, які зайняті
обслуговуванням заявок.
,
де
– загальне число повідомлень в момент
часу
;
– це кількість приладів, які зайняті
обслуговуванням заявок.
Пріоритетні системи МО. Допустимо, що в систему МО поступають вимоги двох типів І і ІІ. Вважають, що вимоги І типу мають відносний пріоритет перед вимогами ІІ типу. Обслуговування відбувається за наступним правилом. Вимоги обох типів утворюють окремі черги, і в момент закінчення обслуговування наступна вимога вибирається із черги вимог ІІ типу. Якщо в системі не має вимог І типу, то приймаються до обслуговування вимога ІІ типу.
Другою формою пріоритету є абсолютний пріоритет. За визначенням, вимоги І типу мають абсолютний пріоритет перед вимогами ІІ типу. Якщо в момент поступлення вимоги І типу обслуговувується заявка ІІ типу, то її обслуговування переривається і терміново починається обслуговуванням заявки І типу. Коли в системі знаходяться як ті, так і другі вимоги, то вони утворюють окремі черги. Розрізняють випадки абсолютного пріоритету з втратами, абсолютного пріоритету з дообслуговування і абсолютного пріоритету з обслуговування спочатку.
