
- •1 Моделі однолінійних систем масового обслуговування
- •1.1 Основні поняття і визначення. Дисципліна обслуговування.
- •1.2 Марківські процеси і ланцюги та їх властивості
- •1.2.1 Поняття марківського процесу і ланцюга
- •1.2.2 Дискретний ланцюг Маркова
- •2. Математична модель процесів народження і загибелі
- •2.1 Рівняння Колмогорова-Чепмена та рівняння Колмогорова
- •2.2 Ергодичні ймовірності процесів народження і загибелі
- •3 Математична модель системи мо з кінцевим числом станів
- •3.1 Зворотні та прямі рівняння Колмогорова
- •3.2 Математичні моделі консервативних систем мо
- •3.3 Обчислення інтенсивностей переходів марківських процесів
- •3.4 Система із n приладів і r із них можуть відновлюватись
- •2. Які величини є елементами інфінітезимальної матриці?
- •4 Моделі багатолінійних систем масового обслуговування
- •4.1 Основні типи систем масового обслуговування
- •4.2 Символіка систем мо
- •4.2 Математичні моделі основних типів систем мо
- •4.3 Багатолінійна система м/м/n/n з обмеженою чергою і обмеженим часом очікування
- •4.4 Обчислення ергодичних розподілів системи мо типу m/m/n/n
- •4.4.1 Багатоканальна система з обмеженою чергою (m/m/n/n)
- •4.4.2 Багатоканальна система з нескінченою чергою і обмеженим часом очікування (m/m/n)
- •4.4.3 Система мо з очікуванням і необмеженою чергою (m/m/n; )
- •5 Оптимальні потоки у мережах
- •5.1 Поняття про мережу і основні визначення
- •5.2 Задача про максимальний потік у мережі
- •5.3 Теореми про оптимальні потоки у мережах
- •5.4 Метод розстановки поміток для знаходження максимального потоку
- •5.5 Модифікований метод розстановки поміток для знаходження максимального потоку
- •5.6 Алгоритм Форда-Фалкерсона знаходження максимального потоку
- •6 Багатополюсні максимальні потоки
- •6.1 Умова реалізації
- •6.2 Аналіз мережі
- •7 Найкоротші ланцюги і потоки мінімальної вартості
- •7.1 Найкоротші ланцюги
- •7.2 Багатополюсні найкоротші ланцюги
- •7.3 Багатополюсні ланцюги максимальної пропускної здатності
- •7.4 Потоки мінімальної вартості
2. Математична модель процесів народження і загибелі
2.1 Рівняння Колмогорова-Чепмена та рівняння Колмогорова
Математичним апаратом опису простої схеми з чергою (рис.1.1) може служити модель, яка носить назву процесів народження і загибелі. Така назва взята із біології, де моделювався процес розвитку певної популяції видів, який залежить від того скільки нових членів популяції народилось, а скільки загинуло.
В нашому випадку число членів популяції буде відповідати числу заявок (повідомлень) в черзі, а народження – прихід певної заявки; загибель – обслужена заявка, яка покидає обслуговуючий прилад (наприклад, сервер).
Якщо випадковий
процес Х(t)
в момент часу
t знаходиться
в стані n,
він може через деякий випадковий проміжок
часу
![]() перейти в одне із сусідніх станів n+1
(кількості заявок в черзі збільшилась
на одиницю) або в n-1
(одна заявка покинула систему).
перейти в одне із сусідніх станів n+1
(кількості заявок в черзі збільшилась
на одиницю) або в n-1
(одна заявка покинула систему).
Допустимо, що Х(t) є марківським процесом із станами 0,1,2,…,n,… і що його ймовірності переходу стаціонарні, тобто
![]() .
.![]()
Крім того допустимо,
що
![]() задовольняє наступними постулатами:
задовольняє наступними постулатами:
1.
![]() при
при
![]() .
.
2.
![]() при
при
![]()
3.
![]() при
при
4.
![]()
3.
![]() >0;
>0;
![]() ,
,
де О(h)
– нескінченно мала величина, така що
![]() .
.
Відмітимо, що
постулат 3 є наслідком двох перших
постулатів. Дійсно, нехай А
– подія, що систему в момент часу t+h
перейде в стан
i+1, а В
– подія, яка відповідає переходу системи
в момент часу t+h
в стан i-1.
Подія
![]() означає, що система перейде в стан А
або в стан В.
Протилежну подію позначимо через
означає, що система перейде в стан А
або в стан В.
Протилежну подію позначимо через
![]() .
Подія С
означає, що система в момент часу t+h
залишиться в стані і.
Обчислимо
.
Подія С
означає, що система в момент часу t+h
залишиться в стані і.
Обчислимо
![]() .
Оскільки
.
Оскільки
![]() ,
то
,
то
![]() .
Враховуючи те, що
.
Враховуючи те, що
![]() і
і
![]() маємо
маємо
![]() .
.
Оскільки
![]() - ймовірності, то
- ймовірності, то
![]() і
і
![]() .
(2.1)
.
(2.1)
Відмітимо одну обставину. Для того щоб перейти із стану i в стан j за час t+s, процес Х(t) в момент t повинен прийняти деяке значення k, а потім за час s, що залишився, перейти в стан j. Це означає, що
![]() .
(2.1)
.
(2.1)
Формула (2.1) носить назву рівняння Колмогорова - Чепмена.
В сумі, що знаходиться
в правій частині рівняння (2.1) виділимо
члени з індексами i-1,
і та і+1,
а
будемо вважати нескінченно малою
величиною. Тоді
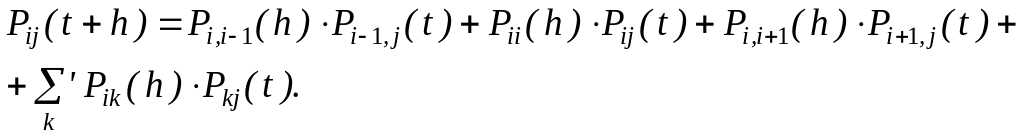
Оцінимо залишкову
суму
![]() в останньому рівнянні. Оскільки
в останньому рівнянні. Оскільки
![]() і
і
![]() ,
то очевидно що
,
то очевидно що
![]() .
З іншої сторони
.
З іншої сторони
![]() .
Звідси знаходимо, що
.
Звідси знаходимо, що
![]() .
Використовуючи постулати 1,2 і 3 знаходимо:
.
Використовуючи постулати 1,2 і 3 знаходимо:
![]() .
Звідси випливає, що
.
Звідси випливає, що
![]() .
.
Отже,
![]() і
і
![]() .
У відповідності з постулатами 1, 2 і 3
.
У відповідності з постулатами 1, 2 і 3
![]() ;
;
![]() і
і
![]() .
Тому
.
Тому
![]()
В останньому рівнянні доданок перенесемо в праву частину і поділимо ліву і праву частину отриманого рівняння на h. Будемо мати
![]() .
.
Переходячи
до граничного
значення
![]() ,
отримуємо
,
отримуємо
![]() ,
,
![]() .
(2.3)
.
(2.3)
Отримані рівняння носять назву зворотних диференціальних рівнянь.
Інша ситуація
виникає при розподілі інтервалу (0; t+h)
на (0; t)
i (t;
t+h).
В цьому випадку![]() .
Як і раніше, у сумі,
що знаходиться у правй частині
виділимо члени з індексами
.
Як і раніше, у сумі,
що знаходиться у правй частині
виділимо члени з індексами
![]() ,
,
,
,
![]()
![]() ,
,
де
![]() - залишкова сума
членів ряду. Зробимо таку заміну індексів
для змінної
- залишкова сума
членів ряду. Зробимо таку заміну індексів
для змінної![]() :
:
![]() .
Тоді
.
Тоді
![]() і
і
![]() .
З врахуванням
першого постулату, будемо мати
.
З врахуванням
першого постулату, будемо мати
![]() .
Перейдемо до
початкових індексів У результаті
отримаємо
.
Перейдемо до
початкових індексів У результаті
отримаємо
![]() .
Розглянемо тепер
величину
.
Розглянемо тепер
величину
![]() .
Для неї зробимо таку заміну індексів:
.
Для неї зробимо таку заміну індексів:
![]() .
Звідси знаходимо
.
Звідси знаходимо
![]() .
Отже,
.
Отже,
![]() .
У відповідності з другим постулатом
.
У відповідності з другим постулатом
![]() .
Якщо перейти до початкових індексів,
то отримаємо
.
Якщо перейти до початкових індексів,
то отримаємо
![]() .
Оцінимо залишкову суму
.
Як і раніше можемо записати ,що
.
Оцінимо залишкову суму
.
Як і раніше можемо записати ,що
![]() .
З іншої сторони
.
З іншої сторони
![]() .
Підставляючи значення
і
та, враховуючи те,
що
.
Підставляючи значення
і
та, враховуючи те,
що
![]() ,
отримаємо
,
отримаємо
![]() .
.
Із останньої рівності знайдемо, що
![]() .
.
Якщо допустити,
що за нескінченно малий проміжок часу
значення величин
і
![]() не змінились, то
не змінились, то
![]() .
Оскільки
.
Оскільки
![]() ,
то
,
то
![]() .
Отже,
.
Отже,
![]() .
Таким чином, можемо
записати, що
.
Таким чином, можемо
записати, що
![]() .
.
Підставляючи
значення
,
![]() та
у останній вираз,
отримаємо
та
у останній вираз,
отримаємо
![]() .
.
Розкривши дужки
і перенісши
![]() у
ліву частину останнього рівняння та
розділивши ліву і праву частину на
,
отримаємо
у
ліву частину останнього рівняння та
розділивши ліву і праву частину на
,
отримаємо
![]() .
.
Переходячи до
граничних значень при
![]() ,
будемо мати
,
будемо мати
![]() ,
,
![]() (2.4)
(2.4)
з
початковими умовами
![]() .
.
Рівняння (2.4) відомі як прямі рівняння Колмогорова.
Якщо в математичній
моделі процесу народження і загибелі
допустити, що
![]() то отримаємо частковий випадок процесу
обслуговування з непереривним часом.
то отримаємо частковий випадок процесу
обслуговування з непереривним часом.
Стан системи при
цьому інтерпретується як довжина черги,
в яку поступають заяви через незалежні
один від одного інтервали часу, що мають
розподіл з параметром λ, і для якої
тривалість часу обслуговування чергового
клієнта є випадковою величиною, що має
експоненціальний розподіл з параметром
![]() ,
який може залежати від довжини черги.
,
який може залежати від довжини черги.
Для одноканальної
системи (з одним обслуговуючим приладом)
![]() .
.
