5.5 Модифікований метод розстановки поміток для знаходження максимального потоку

Тепер ми розглянемо модифікацію методу розстановки поміток, яка придатна для будь-яких неорієнтованих мереж з дійсними пропускними здатностями.

Крок 1. Вилучимо із мережі всі дуги, для яких виконується умова ; такі дуги будемо називати насиченим потоком. (Насправді немає насичених потоків, так як ).

Крок 2. Використовуючи будь-які дуги, із тих що залишились, знаходимо за допомогою методу розстановки поміток довільний шлях; направляємо по ньому максимально можливий потік. Якщо такий шлях знайшовся, то переходимо до кроку 1; якщо же ні, то до – 3.

Крок 3. Відновлюємо у мережі раніше вилучені дуги (тобто дуги насищенні потоками). Знаходимо деякий шлях із до , по якому можна збільшити потік, і направляємо туди максимально можливий потік. Якщо такий шлях знайшовся, то переходимо до кроку 1; у протилежному випадку алгоритм закінчений і знайдений шлях оптимальний.

Тепер наведемо модифікацію методу розстановки поміток. Для зручності будемо вважати, що мережа, яка вміщує вузлів, має дуг, хоч серед них можуть бути дуги з нульовою пропускною здатністю. Якщо заданий потік у деякій мережі, то будемо використовувати символ для позначення такої мережі разом з її потоком. В мережі дуга може бути насиченою і тоді можна вважати, що дуги у мережі не існує, так як неможливо направити потік із вузла у вузол по дузі . Так як можна направити потік із в , то можна допустити, що в є дуга з пропускною здатністю . У подальшому, говорячи про мережу , будемо мати на увазі мережу, яка відрізняється від початкової, в якій ще не було потоку. Метод розстановки поміток, таким чином, породжує деяку послідовність мереж: , , …, , де - максимальний потік. Потік отримують із потоку шляхом добавлення до мережі деякого шляху, який збільшує потік.

При розгляді методу розстановки поміток необхідно у певному порядку розглядати відмічені вузли. Будемо дотримуватись правила «першим відмічений – першим переглянутий» При використанні цього правила кожний раз будемо отримувати шлях з наростаючим потоком, який вміщує мінімальне число дуг (якщо потік у мережі ще не максимальний). Зробимо одне уточнення. Якщо , , , …, - деякий шлях, який збільшує потік, то визначимо наступним чином: . При такому модифікованому визначенні помітки у крайньому випадку одна дуга на шляху, яка збільшує потік, виявиться насиченою потоком.

5.6 Алгоритм Форда-Фалкерсона знаходження максимального потоку

Крок 1. Встановити попередника кожного вузла і резерв за допомогою символу – (не відмічено). Вузол відмічений, коли його резерв не позначений символом – . Резерв вузла прирівнюємо до . Це робиться для того, щоб резерв вузла не обмежував резерви інших вузлів. Сформувати множину .

Крок 2. Якщо - пуста множина, то потік максимальний. Якщо не пуста множина, то вибираємо будь-який елемент із і вилучаємо його. Допускаємо, що цей елемент дорівнює .

Крок 3. Якщо не відмічений, ( ) – дуга і . Покласти . Встановити попередника вузла в . Якщо , добавити в .

Крок 4. Якщо не відмічений, ( ) – дуга і . Покласти . Встановити попередника вузла в ; добавити в .

Крок 5. Якщо відмічений, то використовуючи функцію передування, вернутись до вершини і до кожної дуги шляху добавити резерв вузла до потоку кожної правильно орієнтованої дуги. І вирахувати резерв із потоку кожної неправильно орієнтованої дуги. Повернутись до кроку 1.

Крок 6. Повернутись до кроку 2.

Приклад 5.4. Для мережі, яка показана на рис. 5.7, знайти максимальний потік за допомогою алгоритму Форда-Фолкерсона. Числа поряд з дугами вказують на їх пропускну здатність

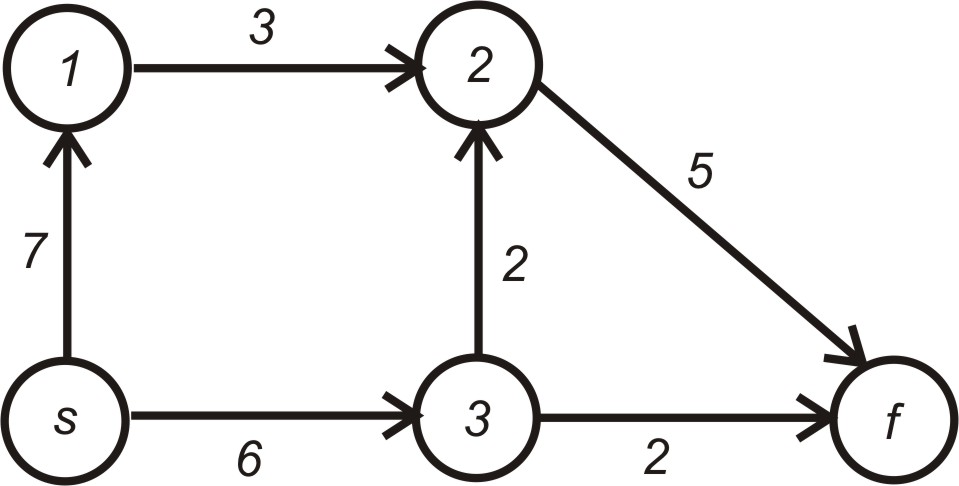
Рисунок 5.7 – Початковий стан мережі

На кроці 1 для кожного вузла встановлюємо попередника і резерв, який дорівнює символу – . Для вузла встановлюємо резерв, який дорівнює , і формуємо множину . Після чого отримаємо мережу, яка показана на рис. 5.8.

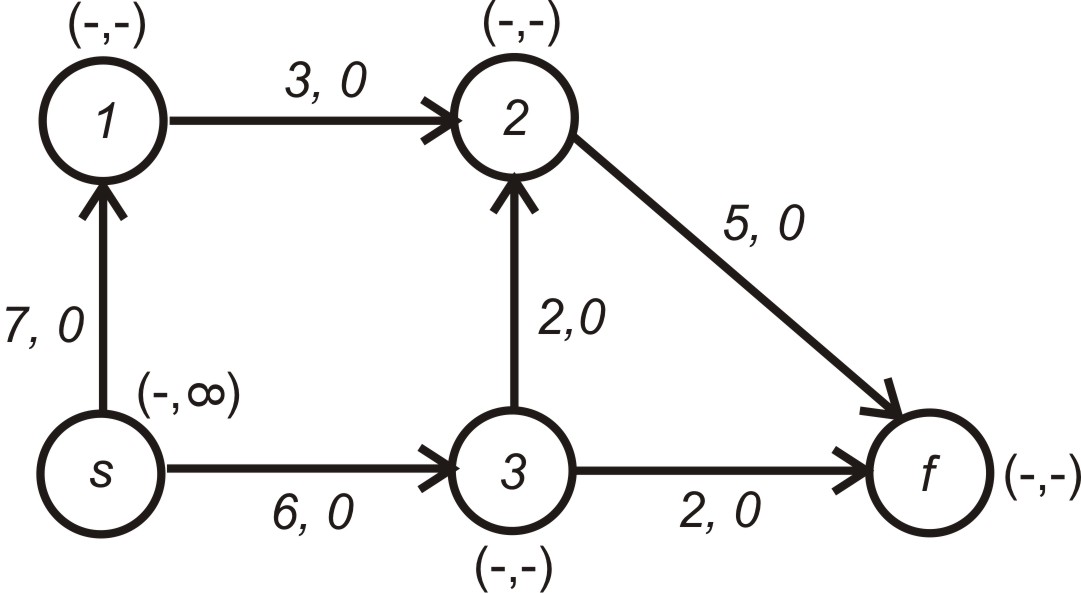
Рисунок 5.8 – Вигляд мережі після першого циклу роботи алгоритму

На кроці 2 провіряємо умову . Оскільки вона виконується, то із множини вилучаємо вузол .

На кроці 3 знаходимо резерв вузла 1 - . Враховуючи значення і будемо мати =7. Беремо вузол як попередник вузла 1. Долучаємо вузол 1 до множини : . Встановлюємо резерв вузла 3 рівним і вибираємо вузол як попередник для вузла 3. Поміщаємо вузол 3 у множину :

Кроки 4 і 5 не використовуємо, тому повертаємося до кроку 2.

На кроці 2 знову провіряємо умову . Оскільки вона виконується, то із множини вибираємо вузол, наприклад, 1. Тепер множина вміщує тільки вузол 3.

На кроці 3 знаходимо резерв вузла 2 - і встановлюємо вузол1 як попередник вузла 2. Поміщаємо вузол 2 у множину , так що .

Знову кроки 4 і 5 не використовуємо, тому повертаємося до кроку 2.

Знову провіряємо умову . Оскільки вона виконується, то із множини вибираємо вузол, наприклад, 2. Тепер множина знову таки вміщує тільки вузол 3.

На кроці 3 вважаємо резерв вузла . Встановлюємо вузол 2 як попередник вузла (стоку). Вузол не включаємо до множини .

На кроці 4 слід відмітити вершину 3, але вона вже відмічена.

На кроці 5 бачимо, що вузол уже відмічений. Утворюємо функцію передування із вузлів, які вилучались на попередніх кроках роботи алгоритму - . Оскільки стік не входить до множини , то його слід долучити до функції передування. Отже, будемо мати такий шлях:

.

Добавляючи резерв стоку до потоку кожної дуги, отримаємо

,

що дає мережу, яка показана на рис. 5.9.

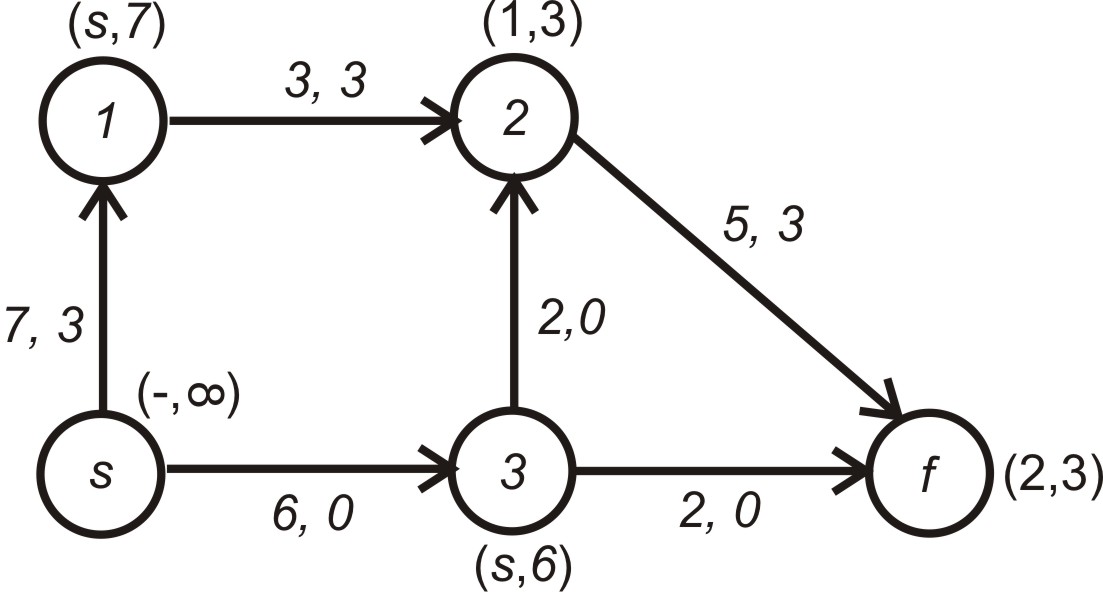
Рисунок 5.9 – Мережа після другого циклу обчислень

Тепер повертаємося до кроку 1, де встановлюємо заново мітки і попередників і вважаємо, що .

На кроці 2 вилучаємо вузол із множини .

На кроці 3 установлюємо резерв вузла 1 рівним

і беремо як попередник вузла 1.Поміщаємо вузол 1 у множину . Резерв вузла 3 залишаємо без зміни і установлюємо вершину як попередник вузла 3. Вузол 3 долучаємо до множини .

Кроки 4 і 5 пропускаємо і повертаємося до кроку 2.

Крок 2. Вилучаємо вершину 1 із множини . Оскільки , то вершину 2 не відмічаємо. Вилучаємо вузол 3 із множини .

На кроці 3 знаходимо резерв стоку : . Знайдемо .

На кроці 4 установлюємо попередника для вузла 2. Таким посередником буде вузол 3. Отже, на кроці 5 вузол буде уже відмічений. Оскільки із множини вилучені вузли , а вузол не включений до множини (умовно вилучений), то матимемо

.

Резерв стоку ( ) до потоку кожної дуги. У результаті отримуємо такий шлях:

.

Поточну ситуацію відтворює рис. 5.10.

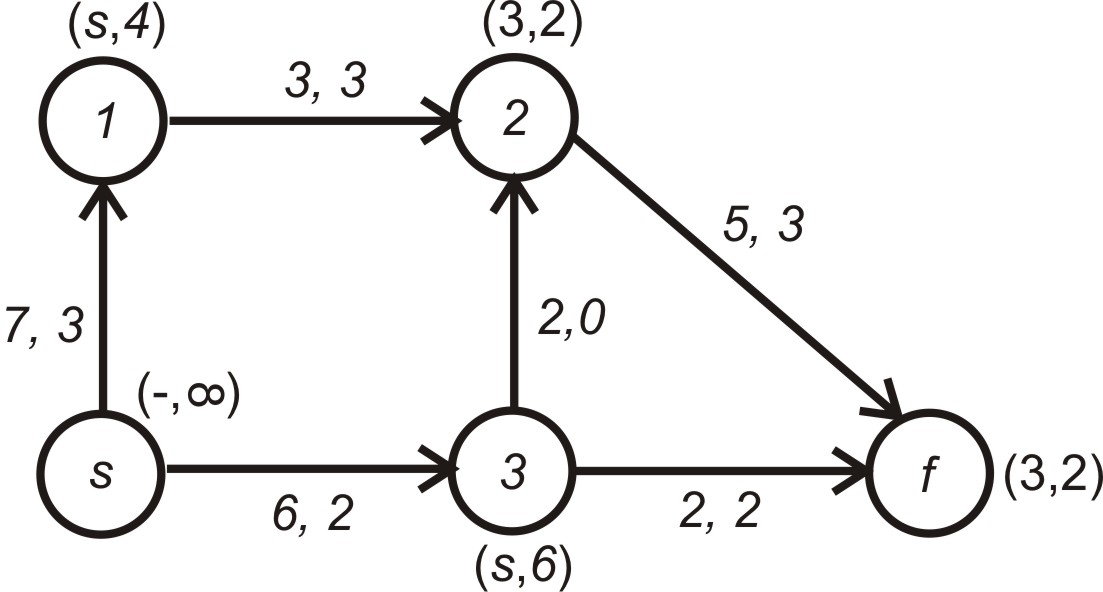
Рисунок 5.10 – Стан мережі після третього циклу обчислень

Знову повертаємося до кроку 1. Встановлюємо заново мітки, як це показано на рис. 5.11. Вузол долучаємо до множини .

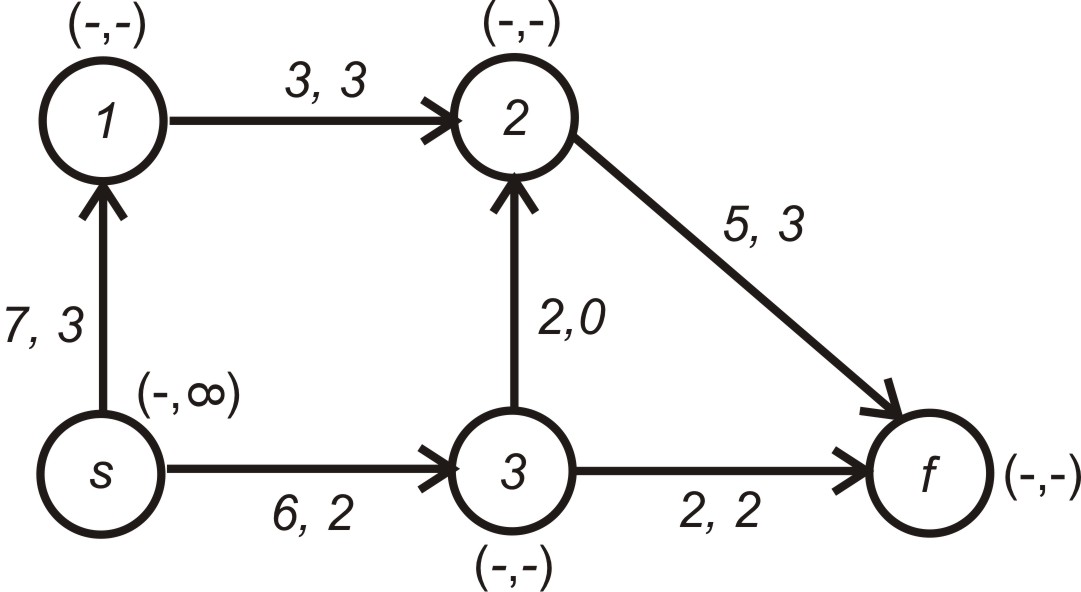
Рисунок 5.11 – Стан мережі на першому кроці

Крок 2. Перевіряємо умову . Оскільки умова виконується, то вузол вилучаємо із множини .

Крок 3. Для вузла 1 значення залишається незмінним, а його попередником буде вузол . Оскільки , то вузол 1 до множини не долучаємо. Встановлюємо резерв вершини 3 таким, що дорівнює . Поміщаємо вузол у множину . Робимо вузол попередником вузла 3. Вузол 3 добавляємо до множини . Тепер . Кроки 4 і 5 пропускаємо і повертаємося до кроку 2.

Крок 2. Перевіряємо умову . Оскільки умова виконується, то вузол 3 вилучаємо із множини . Знаходимо резерв вершини 2:

. Як попередника вузла 2 беремо вузол 3. Поміщаємо вузол 2 у множину : .

Крок 3. Знаходимо резерв вузла (вузол не відмічений) - . Попередником вузла буде вузол 2. Оскільки вузол є стоком, то його не поміщаємо у множину . Кроки 4 і 5 пропускаємо і повертаємося до кроку 2.

Крок 2. Оскільки (множина не пуста), то вузол 2 вилучаємо із множини . Крок 3 пропускаємо і переходимо до кроку 4.

Крок 4. Так як вузол відмічений, то отримуємо функцію передування, яку утворюють вилучені із множини вузли і стік :

.

До потоку кожної дуги добавимо резерв стоку - . У результаті отримаємо

.

Поточну ситуацію відтворює рис. 5.12.

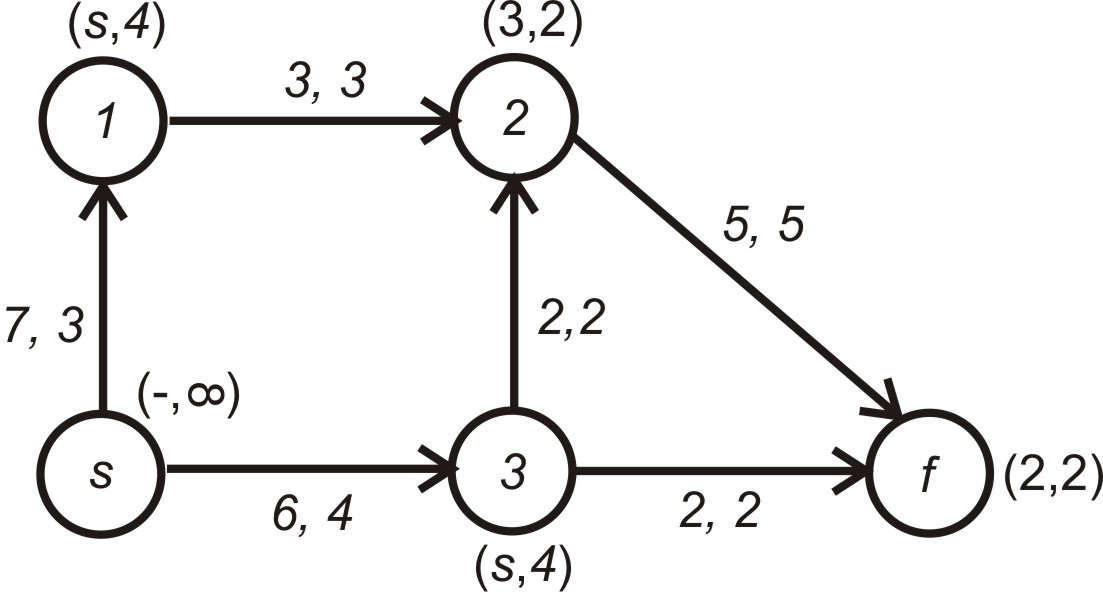
Рисунок 5.12 – Стан мережі після четвертого циклу обчислень

Повертаємося до кроку 1. Встановлюємо заново відмітки і попередників (див. рис 5.11) і вважаємо, що . На кроці 2 вилучаємо вузол із множини ( ). Як і раніше на кроці 3 знаходимо резерв вузла 1, який буде рівним 4, тобто . Джерело буде попередником для вузла 1. Вузол 1 поміщаємо у множину . Встановлюємо також резерв вузла 3 - і поміщаємо вузол 3 у множину . Повертаємося до кроку 2. Вибираємо вузол 1 із множини . Оскільки потік із вузла 1 до вузла 2 дорівнює пропускній здатності , то відмітити вузол 2 неможливо. Тому повертаємося до кроку 2. Вузол 3 вилучаємо із множини . Оскільки виконуються умови і , неможливо відмітити вузли 2 і . Знову повертаємося до кроку 2, але множина пуста. Процес закінчений. Кінцевий потік показаний на рис. 5.13.

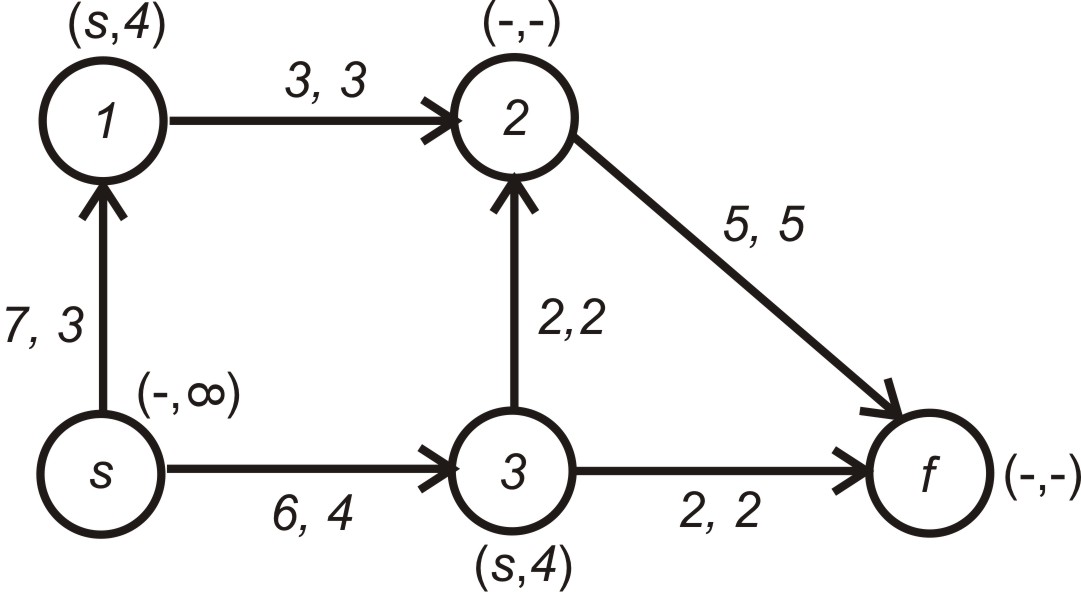
Рисунок 5.13 – Кінцевий стан мережі

Приклад 5.5. Для мережі, яка показана на рис. 5.14 знайти максимальний потік.

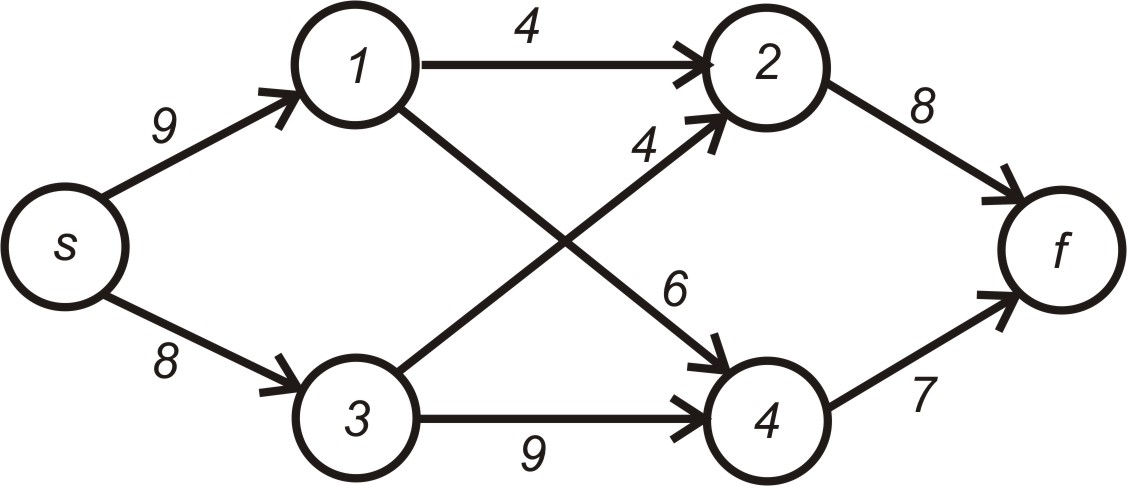
Рисунок 5.14 – Початковий стан мережі

Перші три цикли виконуються так же як і у прикладі 5.4, то дамо їх короткий опис. У першому циклі відмічаємо , , 2(1, 4), , 4(1, 6) і . Це дає шлях

.

Так як резерв вузла дорівнює 4, то

,

що показано на рис. 5.15.

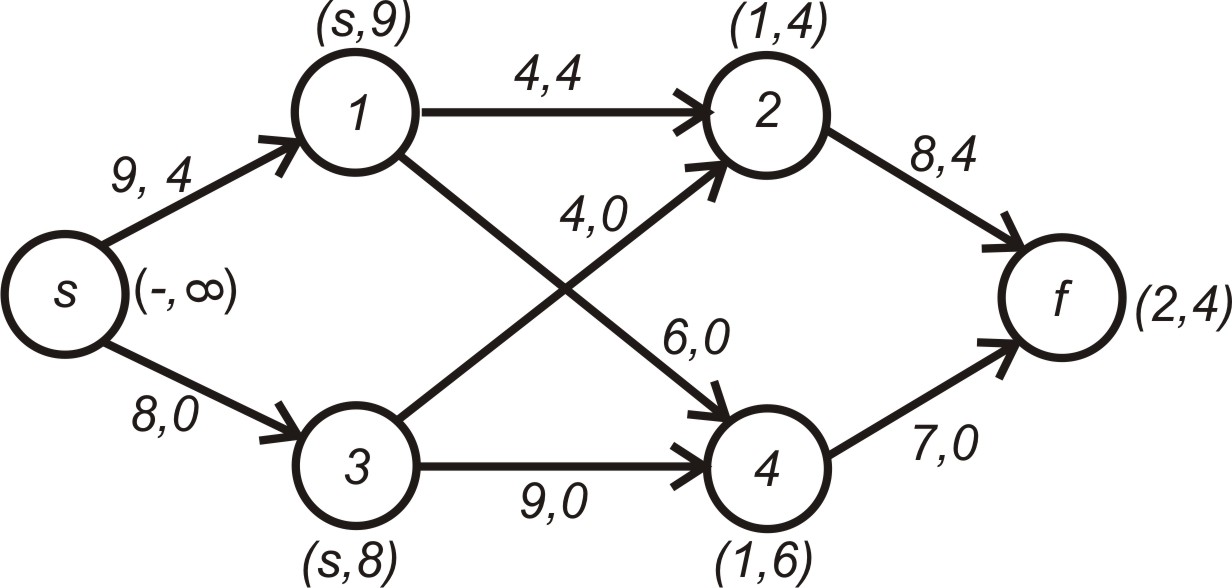
Рисунок 5.15 – Стан мережі після першого циклу

Виконання другого циклу приводить до появи таких міток: , , 2(3, 4), , 4(3, 8) і . Це дає шлях

.

Так як резерв вузла дорівнює 7, то добавимо це значення до кожного потоку

.

Ситуація у мережі після другого циклу показана на рис. 5.16.

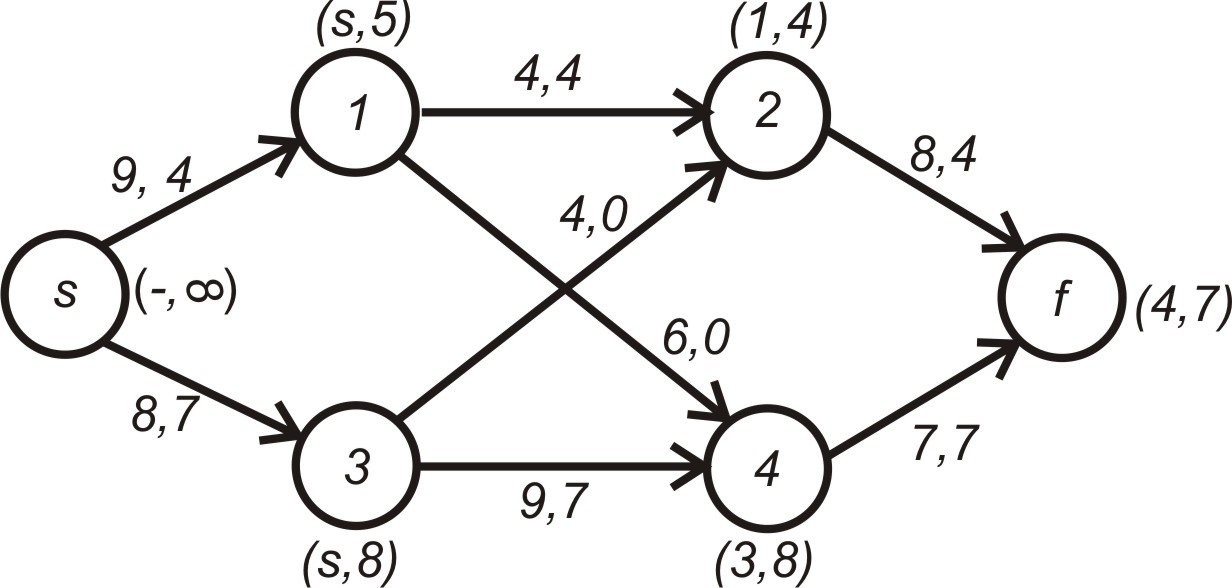
Рисунок 5.16 – Стан мережі після другого циклу

Після третього циклу отримуємо мітки: , 1( , 5), 2(3, 1), , 4(3,1) і . Визначаємо шлях

.

До кожного потоку додаємо резерв вузла , який дорівнює 1. У результаті отримаємо

.

Поточна ситуація з мережею показана на рис. 5.17.

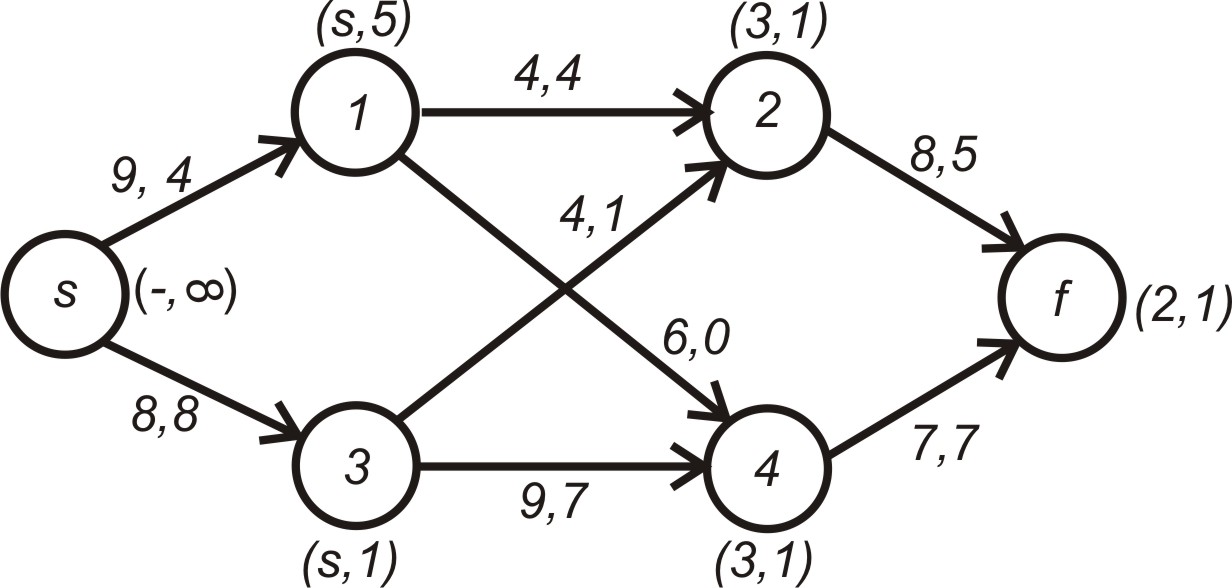
Рисунок 5.17 – Стан мережі після третього циклу

У подальших обчисленнях присутні певні нюанси, яких не було у попередньому прикладі, тому подальший опис буде детальнішим.

Відмітимо 1( , 5), але вузол 3 відмітити неможливо; поміщаємо вузол 1 у множину . При вилученні вузла 1із множини неможливо відмітити вузол 2, але можна відмітити вузол 4(1, 5); поміщаємо вузол 4 у множину . Вилучаємо 4 із , неможливо відмітити вузол , але так як вузол 3 ще не відмічений, його можна відмітити. Оскільки дуга (4, 3) орієнтована неправильно, то у відповідності з кроком 4 її резерв обчислюється за формулою . Враховуючи те, що і , отримуємо . Вузол 4 буде попередником вузла 3. Вузол 3 поміщаємо у множину . Виводимо вузол 2 із множини . Тепер маємо єдину можливість - відмітити вузол 2(3,3) і помістити його в . Вилучаємо вузол 2 із множини і відмічаємо . На цьому закінчуємо поточний цикл і за його результатами отримуємо шлях

.

До отриманих значень потоків додаємо резерв стоку , який дорівнює 3, за винятком дуги (3, 4). Потік цієї дуги має протилежний напрямок, тому із його значення 7 вираховуємо резерв стоку – 3. Отримаємо

.

Результат поточних обчислень відтворює рис. 5.18.

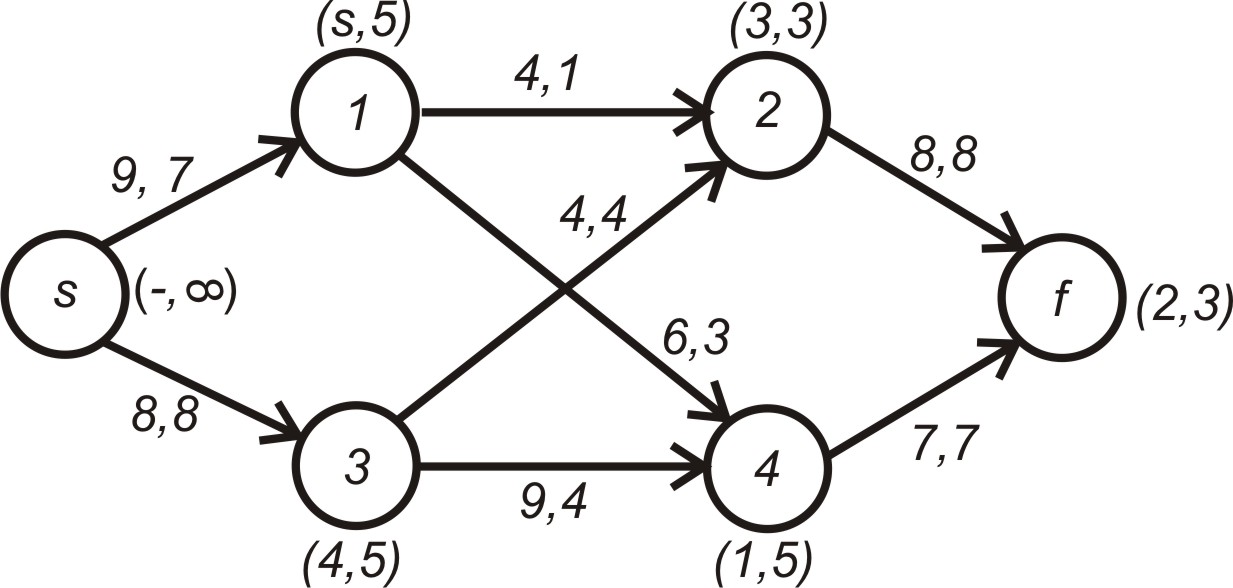
Рисунок 5.18 – Результат поточних обчислень

Починаємо останній цикл обчислень. Спочатку . Вилучаємо вузол із множини , відмічаємо вузол 1( , 5) і поміщаємо 1 в . Вилучаємо вузол 1 із множини , відмічаємо 4(1,2), 2(1, 2) і поміщаємо вузли 2, 4у множину . Вилучаємо 4 із . Знаходимо і відмічаємо вузол 3(4, 2). Поміщаємо 3 в . На наступному кроці із вилучаємо 3 і бачимо, що неможливо виконати ні один із кроків, які залишились, тому повертаємось до кроку 2. Наступним із видаляємо 2, але ми не можемо виконати ні один із кроків, які залишились і повертаємось до кроку 2. Множина пуста, тому алгоритм закінчений. Кінцевий стан мережі показаний на рис. 5.19.

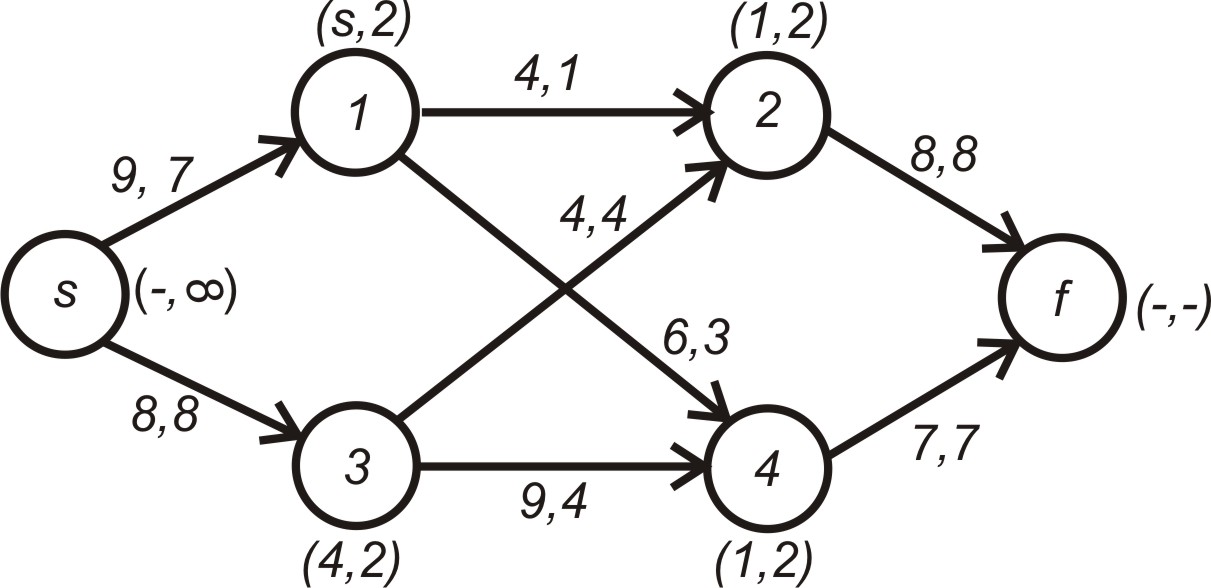
Рисунок 5.19 – Кінцевий стан мережі