5.3 Теореми про оптимальні потоки у мережах

У тому випадку, коли мережа є ланцюгом , , , , …, з джерелом і стоком , максимальна величина потоку, яка може бути пропущена через мережу, обмежується мінімальною із пропускних можливостей дуг цієї мережі. Дуга з мінімальною пропускною можливістю буде вузьким місцем у довільній мережі.

Введемо поняття перетину мережі. Нехай - деяка підмножина вузлів мережі, а - доповнення підмножини ^. Тоді перетином називають мінімальне число дуг, вилучення яких порушує зв’язність мережі. Говорять, що перетин відділяє джерело від стоку , якщо і .

Пропускною здатністю (величиною) січення називається , де сума береться за всіма орієнтованими дугами, що ведуть із в , і за всіма неорієнтованими дугами, які з’єднують і . Відмітимо, що при визначенні перерізу ми враховували всі дуги між множиною і множиною , а при визначенні пропускної здатності перерізу врахували тільки пропускні можливості дуг із в і не враховуємо орієнтовані дуги із в . Тому у загальному випадку .

Теорема про максимальний потік. У будь-якій мережі величина максимального потоку із джерела до стоку дорівнює пропускній можливості мінімального перерізу, який розділює і .

Позначимо через множину невід’ємних чисел , які задовольняють обмеженням (5.1), (5.2). Будемо вважати шлях із в таким, що збільшує потік , якщо на всіх прямих дугах і на всіх протилежних дугах цього шляху.

Як наслідок із наведеної теореми витікає наступне твердження:

Потік максимальний тоді і тільки тоді, коли не існує шляху, який збільшує .

Величина максимального потоку у будь-якій мережі приймає, безумовно, єдине значення. Тим не менше може існувати декілька різних максимальних потоків ,які мають одинакові значення. Може існувати і декілька мінімальних січень у мережі.

Розглянемо, наприклад, мережу на рис. 5.3. Допустимо, що всі дуги мають пропускні здатності, рівні одиниці. Тоді і дуга і дуга є мінімальними січеннями. Величина мінімального потоку, звичайно же, дорівнює одиниці. Але максимальних потоків тут декілька, наприклад , інші ; або ; інші .

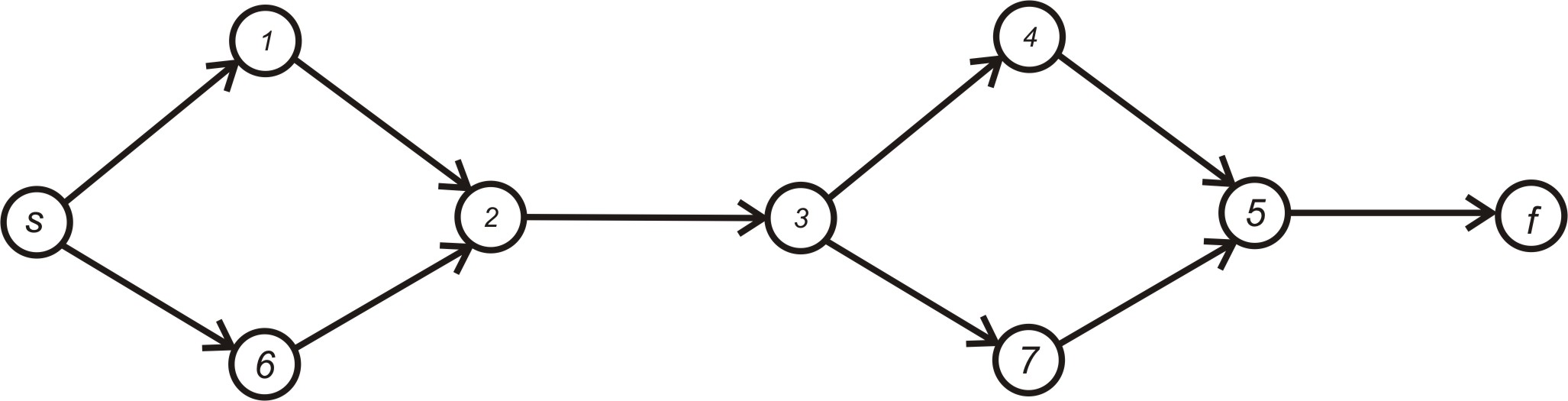
Рисунок 5.3 – мережа з двома мінімальними січеннями

Теорема про мінімальні січення. Нехай і - мінімальні січення, які розділюють і . Тоді і - також мінімальні розрізи, які розділюють і .

Так як існує багато мінімальних січень, то виникає питання: про яке мінімальне січення іде мова у теоремі про максимальний потік? Нехай - всі мінімальні січення, які розділюють та і - мінімальне січення, про яке йде мова у тій же теоремі. Тоді .

5.4 Метод розстановки поміток для знаходження максимального потоку

В основі методу лежать теореми про максимальні потоки і мінімальні січення, які сформульовані раніше. Меток розстановки поміток починається з довільного потоку (як початковий – можна взяти нульовий потік). Потім здійснюється спроба знайти потік з більшим значенням. Обчислення закінчуються тоді, коли отриманий максимальний потік. Суть алгоритму у тому, що здійснюється систематичний пошук всіх можливих шляхів, які збільшують потік. Пошук таких шляхів здійснюється за допомогою процедури «розстановки поміток». Вузли отримують спеціальні «помітки», які вказують напрямок, у якому може бути збільшений деякий дуговий потік. Після того як знайдений деякий шлях, що збільшує потік, визначають величину максимальної пропускної здатності цього шляху; дальше потік збільшують на цю величину, а всі помітки на вузлах стирають. Потім починається розстановка нових поміток, виходячи із тільки що отриманого потоку. Алгоритм складається із двох кроків.

Крок 1. (розстановка поміток). На кроці 1 кожний вузол знаходиться в одному із трьох станів: «відмічений і переглянутий», «відмічений і не переглянутий» і «не відмічений». Спочатку всі вузли не відмічені. Помітка довільного вузла завжди складається із двох частин. Перша частина – індекс вузла , який вказує, що є можливість направити потік із в . Друга частина поміток – число, яке вказує максимальну величину потоку, який можна направити із джерела у не порушуючи обмежень на пропускні здатності дуг. Це друге число будемо називати резервом вершини .

Перш за все джерело отримує помітку . Перша частина цієї помітки означає, що можна направити потік із вузла у той же вузол; символ означає, що величина потоку не обмежена зверху. Тепер вузол «відмічений і не переглянутий», а всі інші вузли «не відмічені».

У загальному випадку вибираємо будь-який відмічений і не переглянутий вузол . Нехай він має помітку або . Два вузли будемо називати сусідніми, якщо вони з’єднані дугою. Із всіх вузлів, які є сусідніми із , виділимо ті вузли , які не відмічені і для яких . Присвоїмо кожному вузлу помітку , де . Такі вузли тепер відмічені і переглянуті. Після цього всім сусіднім з вузлам , які не відмічені і для яких , приписується помітка , де . Такі вузли тепер також відмічені і не переглянуті. Тепер всі вузли, що є сусідніми з , мають помітки. Тоді вузол вважається відміченим і переглянутим і його можна у подальшому не розглядати на цьому кроці. Може трапитись, що деякі сусідні з вузли відмічені, а інші не можуть бути відмічені (або ж всі сусідні з вузли не можуть бути відмічені); у цих випадках вузол також вважається відміченим і переглянутим. Знаки «+» і «-» у першій частині поміток показують як повинен бути змінений потік на кроці 2.

Продовжимо приписувати помітки вузлам, які є сусідніми для відмічених і не переглянутих вузлів до тих пір, поки вузол стане відміченим або ж не можна буде більше відмітити ні один вузол і стік виявиться невідміченим. Якщо не може бути відміченим, то не існує шляху із в , який збільшує потік, і, як наслідок, побудований потік максимальний. Якщо ж відмічений, то на кроці 2 можна знайти шлях , який збільшує потік.

Крок 2 (зміна потоку). Допустимо, що стік має помітку . Тоді замінимо на . Якщо ж він має помітку , то замінимо на . Потім у будь-якому із цих випадків переходимо до вузла . Взагалі якщо вузол має помітку , то замінимо на і перейдемо до вузла ; якщо ж вузол має помітку , то замінимо на і перейдемо до . Продовжимо ці дії до досягнення джерела .

Кроки 1 і 2 повторюють до тих пір поки збільшення потоку стає неможливим.

Зробимо одне важливе застереження. Якщо обчислення почались з цілочисленного потоку , то всі наступні потоки (зокрема, максимальний), які отримані при роботі даного алгоритму, будуть також цілочисленними. Цей простий, але важливий факт відомий як теорема про цілочисельність: якщо пропускні здатності дуг цілочисленні, то існує максимальний потік, який то же цілочисельний. У даному алгоритмі чілочисельність забезпечує збіжність процесу обчислень за кінцеве число кроків.

Приклад 5.3. Розглянемо мережу, яка показана на рис. 5.4. Кожній орієнтованій дузі поставлено у відповідність два числа. Перше із них – пропускна здатність дуги , а друге – початковий потік по дугам . (Як початковий потік можна використати будь-який потік, який задовольняє умовам (5.1) – (5.2), зокрема, можна було би взяти для всіх ).

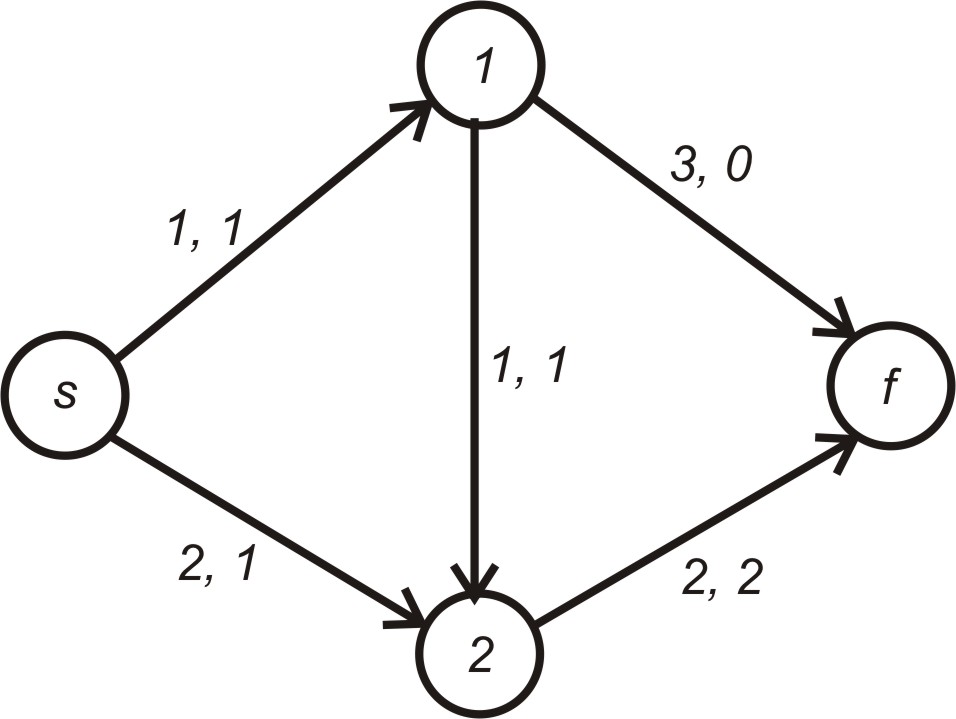
Рисунок 5.4 – Початковий стан мережі

Крок 1. Припишемо вузлу помітку . Вузол має два сусідніх вузла і . Помітити ми не можемо, так як і , а це означає, що немає дугового потоку . Вузлу присвоюємо помітку . Оскільки , то помітка вузла буде такою: . Знаходимо . Тепер вузол підмічений і переглянутий, а вузол відмічений і не переглянутий.

Вузол має два не відмічених сусідніх вузла - і . Вузол у даний момент не може бути відміченим, а вузол отримує мітку , оскільки і .Тепер вузол відмічений і переглянутий, а - відмічений і не переглянутий. Вузол має тільки один сусідній не відмічений - . Вузол повинен отримати помітку , оскільки .

Результат розстановки поміток на першому кроці показаний на рис. 5.5. Так як вузол став відміченим, то переходимо до кроку 2.

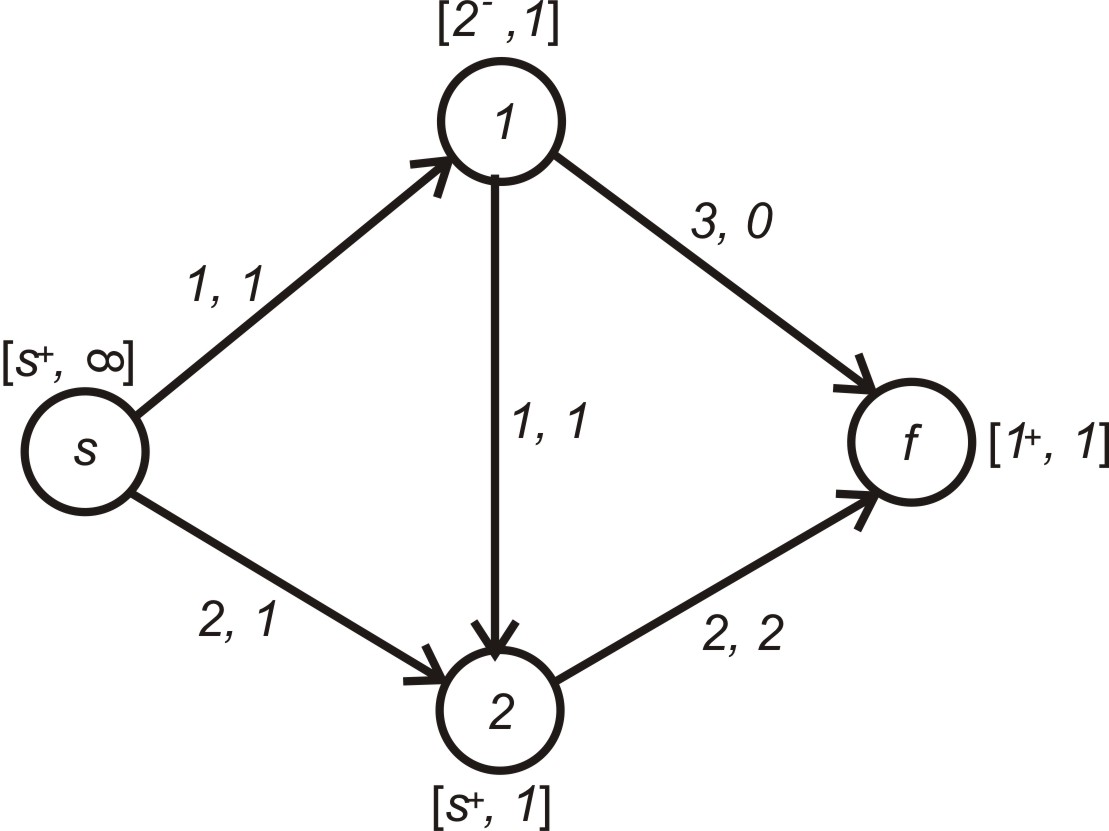
Рисунок 5.5 – Результат розстановки поміток на першому кроці

Крок 2. Так як помітка вузла - , то збільшуємо на 1. у результаті отримаємо . Переходимо до вузла , який має помітку , і зменшуємо на одиницю. Отримаємо: . Переходимо до вузла з поміткою і додаємо до 1 до . У результаті будемо мати . Кінцевий результат операції зміни потоку показаний на рис. 5.6.

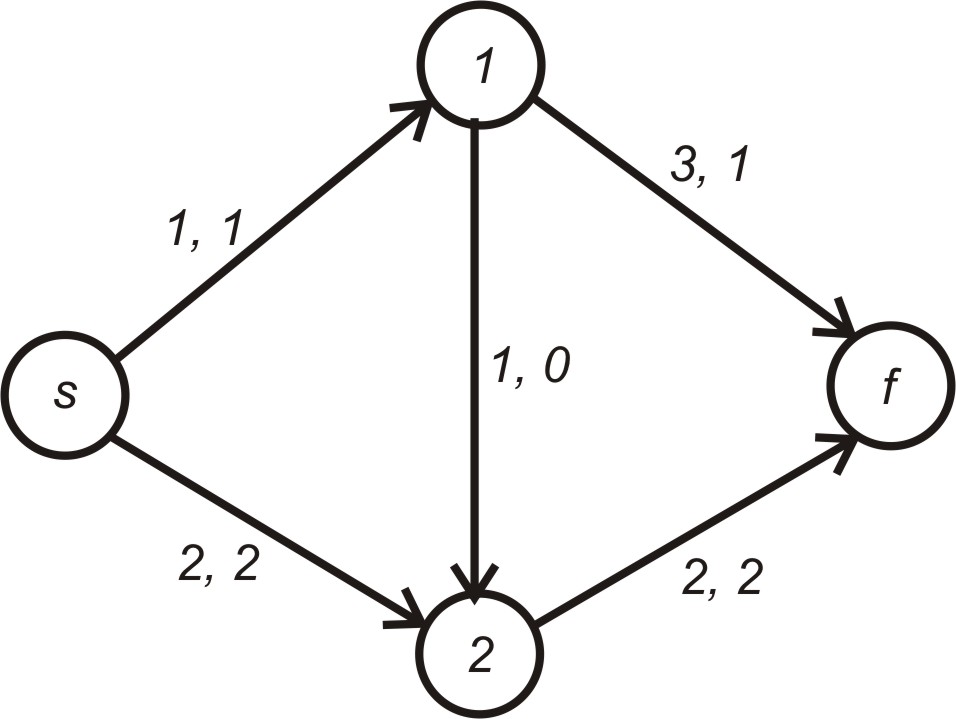
Рисунок 5.6 – Кінцевий результат операції зміни потоків

Крок 3. Присвоюємо помітку вузлу . Тепер вузли і не можуть бути відміченими і вузол буде невідміченим. Кінець алгоритму.

У цьому алгоритмі ми отримали мінімальне січення , де - єдиний вузол , а - три вузли , і .

Якщо пропускні здатності не цілі числа, то алгоритм може не бути кінцевим і може навіть не збігатись до максимального потоку.