
- •1 Моделі однолінійних систем масового обслуговування
- •1.1 Основні поняття і визначення. Дисципліна обслуговування.
- •1.2 Марківські процеси і ланцюги та їх властивості
- •1.2.1 Поняття марківського процесу і ланцюга
- •1.2.2 Дискретний ланцюг Маркова
- •2. Математична модель процесів народження і загибелі
- •2.1 Рівняння Колмогорова-Чепмена та рівняння Колмогорова
- •2.2 Ергодичні ймовірності процесів народження і загибелі
- •3 Математична модель системи мо з кінцевим числом станів
- •3.1 Зворотні та прямі рівняння Колмогорова
- •3.2 Математичні моделі консервативних систем мо
- •3.3 Обчислення інтенсивностей переходів марківських процесів
- •3.4 Система із n приладів і r із них можуть відновлюватись
- •2. Які величини є елементами інфінітезимальної матриці?
- •4 Моделі багатолінійних систем масового обслуговування
- •4.1 Основні типи систем масового обслуговування
- •4.2 Символіка систем мо
- •4.2 Математичні моделі основних типів систем мо
- •4.3 Багатолінійна система м/м/n/n з обмеженою чергою і обмеженим часом очікування
- •4.4 Обчислення ергодичних розподілів системи мо типу m/m/n/n
- •4.4.1 Багатоканальна система з обмеженою чергою (m/m/n/n)
- •4.4.2 Багатоканальна система з нескінченою чергою і обмеженим часом очікування (m/m/n)
- •4.4.3 Система мо з очікуванням і необмеженою чергою (m/m/n; )
- •5 Оптимальні потоки у мережах
- •5.1 Поняття про мережу і основні визначення
- •5.2 Задача про максимальний потік у мережі
- •5.3 Теореми про оптимальні потоки у мережах
- •5.4 Метод розстановки поміток для знаходження максимального потоку
- •5.5 Модифікований метод розстановки поміток для знаходження максимального потоку
- •5.6 Алгоритм Форда-Фалкерсона знаходження максимального потоку
- •6 Багатополюсні максимальні потоки
- •6.1 Умова реалізації
- •6.2 Аналіз мережі
- •7 Найкоротші ланцюги і потоки мінімальної вартості
- •7.1 Найкоротші ланцюги
- •7.2 Багатополюсні найкоротші ланцюги
- •7.3 Багатополюсні ланцюги максимальної пропускної здатності
- •7.4 Потоки мінімальної вартості
5 Оптимальні потоки у мережах
5.1 Поняття про мережу і основні визначення
Мережа складається із множин вершин і дуг (ребер), які з’єднують ці вузли. Якщо дуга має певну орієнтацію, то вона називається орієнтованоною або направленою. У тому випадку, коли орієнтація дуги не задана, то вона носить назву неорієнтованої. Неорієнтовану дугу називають ребром. На рис. 5.1 показана мережа із чотирьох вузлів і шести орієнтованих дуг.
Символом
![]() будемо позначати
- тий вузол, а
будемо позначати
- тий вузол, а
![]() - дугу, яка веде із вузла
до
- дугу, яка веде із вузла
до
![]() .
Якщо вузли
мережі з’єднують ребра, то їх можна
позначати як символом
,
так і символом
.
Якщо вузли
мережі з’єднують ребра, то їх можна
позначати як символом
,
так і символом
![]() .
.
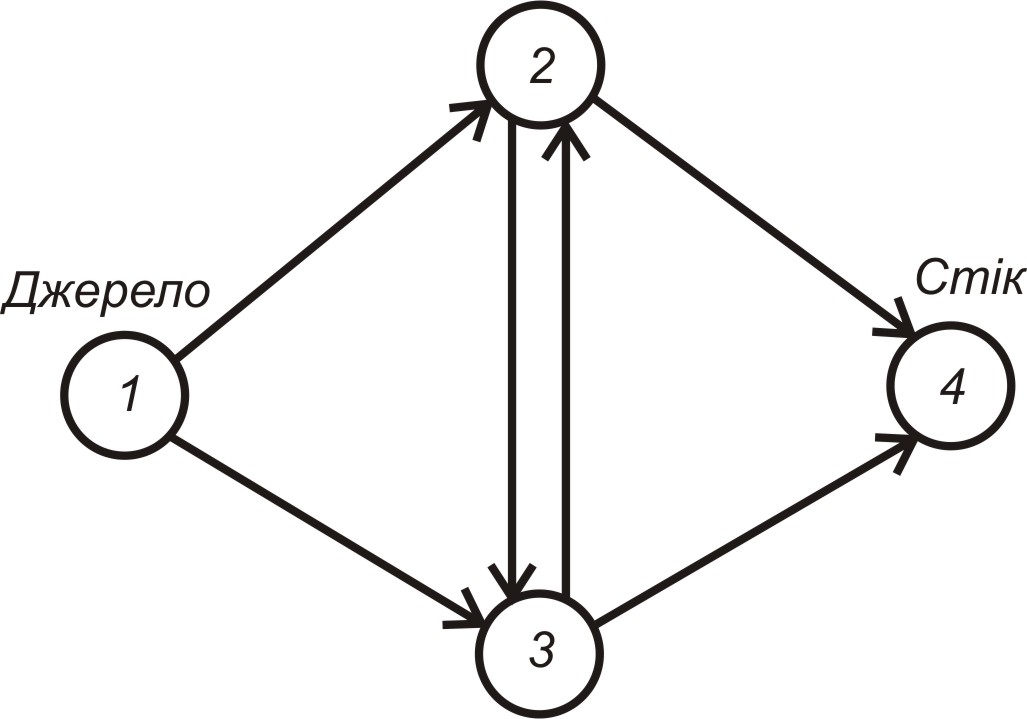
Рисунок 5.1 – Мережа з орієнтованими дугами
Мережа називається
зв’язаною, якщо при будь-якому розбитті
множини вузлів на дві підмножини
і
![]() знайдеться дуга
або
така, що
знайдеться дуга
або
така, що
![]() і
і
![]() .
Іншими словами, мережа буде зв’язаною,
якщо є шлях між двома будь-якими вершинами.
Будемо вважати, що між двома вузлами
і
є не більше однієї орієнтованої і однієї
неорієнтованої дуги або лише одна
неорієнтована дуга (ребро). Не будемо
розглядати мережі з петлями.
.
Іншими словами, мережа буде зв’язаною,
якщо є шлях між двома будь-якими вершинами.
Будемо вважати, що між двома вузлами
і
є не більше однієї орієнтованої і однієї
неорієнтованої дуги або лише одна
неорієнтована дуга (ребро). Не будемо
розглядати мережі з петлями.
Послідовність
дуг і вузлів мережі
![]() ,
,
![]() ,
,
![]() ,
,
,
,
![]() ,
…,
,
…,
![]() ,
,
![]() ,
,
![]() ,
яка починається у вузлі
і закінчується вузлом
називається ланцюгом
або орієнтованим
ланцюгом. Якщо
,
яка починається у вузлі
і закінчується вузлом
називається ланцюгом
або орієнтованим
ланцюгом. Якщо
![]() ,
то така послідовність вузлів і вершин
називається орієнтованим
циклом.
Ланцюг називається простим,
якщо він не вміщує циклів.
,
то така послідовність вузлів і вершин
називається орієнтованим
циклом.
Ланцюг називається простим,
якщо він не вміщує циклів.
Приклад 5.1
● На рис 5.1
послідовність
,
,
,
![]() ,
,
![]() є ланцюгом; ланцюгом є також послідовність
,
є ланцюгом; ланцюгом є також послідовність
,
![]() ,
,
,
,
![]() ,
.
,
.
● Послідовність
,
![]() ,
,
(рис. 5.1) буде циклом.
,
,
(рис. 5.1) буде циклом.
У мережах розрізняють ланцюг і шлях. На відміну від ланцюга шляхом мережі можна рухатись і у напрямку, який протилежний орієнтації дуг. Для неорієнтованих мереж поняття ланцюга і шляху співпадають.
Приклад 5.2
● На рис 5.1 послідовність , , , , є шляхом.
Кожній дузі можна
поставити у відповідність деяке додатне
число
![]() ,
яке означає пропускну
здатність дуги (ребра).
У мережі виділяють два особливих вузла.
Один із них називається джерелом
(source)
і позначається
,
яке означає пропускну
здатність дуги (ребра).
У мережі виділяють два особливих вузла.
Один із них називається джерелом
(source)
і позначається
![]() ;
другий називається стоком
(flow)
і позначається
;
другий називається стоком
(flow)
і позначається
![]() .
.
5.2 Задача про максимальний потік у мережі
Перш ніж сформулювати задачу про максимальний потік у мережі введемо спочатку поняття потоку у мережі. Потоком у мережі із джерела до стоку називається множина невід’ємних чисел (кожне із яких поставлено у відповідність деякій дузі мережі) за умови, що ці числа задовольняють наступним лінійним обмеженням:
 (5.1)
(5.1)
![]() ,
,
![]() для всіх
,
.
(5.2)
для всіх
,
.
(5.2)
В обмеженнях (5.1) перша сума береться по дугам, які ведуть в , а друга – по вузлам, які виходять із .
Невід’ємне число
![]() ,
яке фігурує в (5.1) називається величиною
потоку. Число
називається потоком по дузі
.
,
яке фігурує в (5.1) називається величиною
потоку. Число
називається потоком по дузі
.
Обмеження (5.1)
виражає той факт, що у кожний вузол (крім
джерела і стоку) приходить скільки
потоку скільки із нього виходить (умова
збереження) (рис. 5.2) Обмеження (5.2) означає,
що потік
по дузі обмежений пропускною здатністю
дуги
![]() .
.
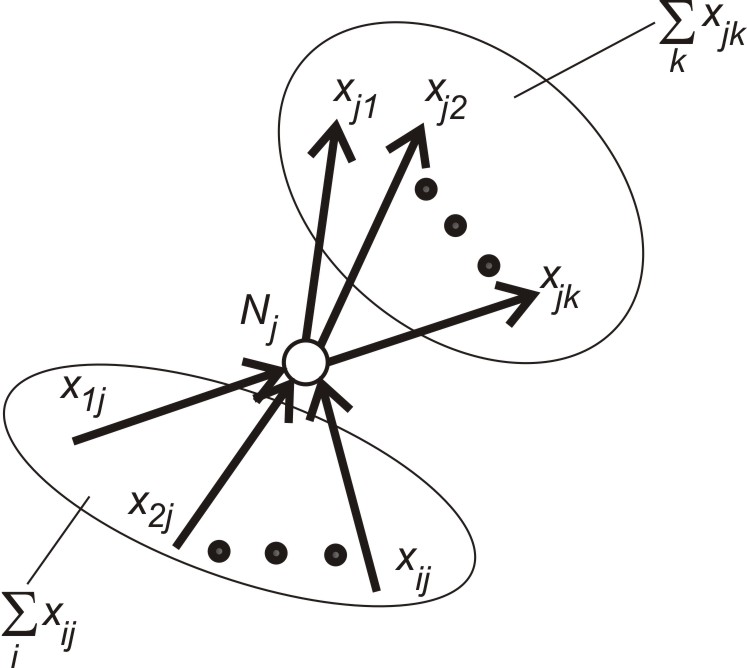
Рисунок 5.2 – Умова збереження потоків у вузлі
Тоді задача пошуку оптимальних потоків у мережі зводиться до максимізації цільової функції
![]() (5.3)
(5.3)
при виконанні обмежень (5.1), (5.2).
