- •Равномерное движение жидкости в открытых
- •Особенности движения воды в открытых руслах
- •Если в выражение для гидравлического радиуса
- •Расчет канализационных труб
- •1.10 Расчет естественных русел на равномерное течение воды
- •1.11 Лимитные значения коэффициента шероховатости
- •Глава II
- •2.1. Неравномерное течение воды в открытых руслах
1.10 Расчет естественных русел на равномерное течение воды
Иногда естественное русло неправильной формы, в котором движение воды неравномерное можно с некоторым приближением заменить руслом правильной формы и считать движение в нем равномерным. При этом: а) заменяют действительное неправильное русло руслом призматической формы; б) уклон дна принимают равным или уклону дна свободной поверхности воды в действительном (естественном ) русле или уклону, полученному в результате осреднения уклонов дна естественного русла; в) полученное условное русло рассчитывают по приведенным выше формулам.
1.11 Лимитные значения коэффициента шероховатости
Обычно расчет проектируемого канала ведут при некотором наиболее вероятном значении коэффициента шероховатости n. Запроектированный канал дополнительно проверяется а) на заведомо большое значение n (n = nmax) в отношении которого можно утверждать: n max > n действ б) на заведомо малое значение n, в отношение которого можно утверждать nmin> n действ.
Выполняя проверку на максимальную шероховатость, получаем предельно возможное максимальное наполнение канала, выполняя проверку на минимальную шероховатость, получаем предельно возможную максимальную скорость течения воды в канале.Величины nmax и nmin могут быть названы лимитными значениями коэффициента шероховатости. Их значения находят по соответствующим таблицам в справочниках по гидравлическим расчетам.
О неоднородности коэффициента шероховатости.
В практике часты случаи когда вдоль смоченного периметра шероховатость неоднородна. Например: откосы дамб, образующих канал покрыты, облицованы бетоном, а дно канала не покрыто такой облицовкой или свободная поверхность канала покрыта льдом, вследствие чего вдоль смоченного периметра будет неоднородная шероховатость. В этом случае шероховатость усредняется:
![]() (1.37)
(1.37)
Глава II
2.1. Неравномерное течение воды в открытых руслах
Движение воды в открытых руслах чаще всего неравномерное, так как по длине потока может изменяться сечение, шероховатость и, следовательно, изменяется средняя скорость и коэффициент Кориолиса.
При неравномерном движении воды
гидравлический уклон потока (![]() ),
пьезометрический уклон (I)
и уклон дна (i) не равны.
),
пьезометрический уклон (I)
и уклон дна (i) не равны.
Примерами неравномерного течения воды в открытых руслах может быть движение воды в реках с изменяющимся живым сечением (на расширениях, сужениях , на переходах от мелких мест – перекатов к глубоким – плесам, при устройстве плотин, мостов, перепадов. При неравномерном движении воды в открытых руслах возможны два противоположных явления:
а) подпор, когда глубины по длине потока возрастают, а скорость течения уменьшается (рис. 2.1)
б) Спад, который получается в каналах и реках перед уступом или резким увеличением уклона и характеризуется уменьшение глубины по длине потока и
у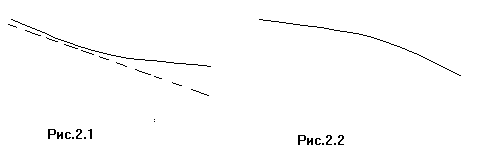 величением
скорости движения воды (рис. 2.2)
величением
скорости движения воды (рис. 2.2)
Кр.подпора
Кр. спада
К
 роме
этого в открытых руслах иногда образуется
гидравлический прыжок, то есть резкое
увеличение глубины потока.
роме
этого в открытых руслах иногда образуется
гидравлический прыжок, то есть резкое
увеличение глубины потока.
2.1 Типы открытых русел
В инженерной практике встречаются русла имеющие различные характеристики. Их можно разделить на две группы:
1. Призматические, когда площадь и форма поперечного сечения русла по длине его неизменны и поперечное сечение потока зависит только от глубины:
= f(h)
2. Непризматические, когда площадь и форма поперечного сечения русла изменяются по его длине. В этом случае площадь поперечного сечения потока зависит и от глубины и от расстояния от начального сечения = f (h,S).
Если поперечный профиль русла очерчивается кривой линией, например параболой, то такое русло можно назвать цилиндрическим. Очевидно, что цилиндрическое русло по своим свойствам аналогично призматическому.
В отношении формы поперечного сечения открытые русла можно разграничить на русла правильной формы и русла неправильной формы.
К руслам правильной формы относятся такие русла, для которых гидравлические элементы потока являются непрерывными монотоно возрастающими функциями глубины потока. Причем каждая из этих функций имеет вполне определенное аналитическое выражение для всего диапазона изменений глубины потока. Этому условию удовлетворяют русла прямоугольные, трапецеидальные, треугольные, параболические, круговые и пр., то есть большинство русел, встречающихся в инженерной практике.
Открытые русла, характеризующиеся полигональным (составным) профилем не удовлетворяют указанным выше условиям и являются, следовательно, руслами неправильной формы.
В отношении уклона дна открытые русла можно разграничить следующим образом:
Русла с прямым уклоном дна i > 0 (рис. 2.3)
Русла с горизонтальным дном i = 0 (рис. 2.4)
Русла с обратным (отрицательным) уклоном дна i < 0 (рис.2.5)



Рис. 2.3 Рис. 2.4 Рис. 2.5
Следует иметь в виду, что при i =0 и i < 0 равномерное движение невозможно. В этих случаях формула Шези теряет физический смысл и вместе с этим теряет смысл термин «нормальная глубина»
2.2 Удельная энергия сечения. Критическая глубина.
С редняя удельная энергия потока в каком-либо живом сечении потока, отнесенная к некоторой горизонтальной плоскости сравнения, как известно, определя- ется следующим уравнением:
![]() (2.1)
(2.1)
Удельной энергией сечения Э0 называется частной значение полной удельной энергии потока, определенное относительно плоскости сравнения,.проходящей через наинизшую точку сечения русла. При плавноизменяющемся течении пьезометрический напор z +p/ одинаков во всех точках живого
сечения. Для указанной плоскости сравнения имеем z + p/ =h и, следовательно, вместо (2.1) имеем:
Э0 = h + V2/2g (2.2)
или Э0 = h + Q2/2g 2 (2.3)
Для прямоугольного русла используется понятие удельного или единичного
расхода:
![]() (2.4)
(2.4)
где Q/b – называется удельным или единичным расходом.
Уравнения (2.2) и (2.3) показывают зависимость удельной энергии сечения от глубины при постоянном расходе. При увеличении глубины потока h первый член уравнения (2.3), представляющий собой величину удельной потенциальной
энергии увеличивается, а второй член, представляющий величину удельной кинетической энергии уменьшается. Глубина потока при данном расходе может изменяться в пределах от 0 до . Рассмотрим изменение удельной энергии сечения при этих колебаниях глубин. Для исследования изменения величины удельной энергии сечения в зависимости от изменения глубины h определим характер изменения функции Э0 = (h), для чего возьмем первую производную от Э0 по h и приравняем ее нулю:
![]() (2.5)
(2.5)
П
 ри
h 0 согласно (2.5) Э0
.
Следовательно, если построить кривую
Э0 = f (h)
в прямоугольных координатах, откладывая
по оси ординат h, а по
оси абсцисс Э0, то эта
кривая асимптотически приближается к
оси абсцисс. При h
0 удельная энергия Э0 .
Однако, здесь следует учесть, что с
увеличением h резко
возрастает 2
и поэтому при достаточно больших h
уравнение (2.5) стремится к уравнению
вида Э0 = h,
то есть прямой, выходящей из начала
координат под углом 450 . Функция
Э0 = f(h)
имеет экстремум, который находим,
взяв производную
ри
h 0 согласно (2.5) Э0
.
Следовательно, если построить кривую
Э0 = f (h)
в прямоугольных координатах, откладывая
по оси ординат h, а по
оси абсцисс Э0, то эта
кривая асимптотически приближается к
оси абсцисс. При h
0 удельная энергия Э0 .
Однако, здесь следует учесть, что с
увеличением h резко
возрастает 2
и поэтому при достаточно больших h
уравнение (2.5) стремится к уравнению
вида Э0 = h,
то есть прямой, выходящей из начала
координат под углом 450 . Функция
Э0 = f(h)
имеет экстремум, который находим,
взяв производную
![]() и приравняв ее нулю:
и приравняв ее нулю:
![]() (2.6)
(2.6)
К
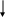
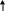
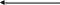
 ак
видно из рис. (2.8), приращение живого
сечения равно d
= Bdh
ак
видно из рис. (2.8), приращение живого
сечения равно d
= Bdh
 Рис .2.7
Рис .2.7
Где В – ширина зеркала воды при глубине h. Следовательно, с учетом (2.6):
![]() (2.7)
(2.7)
Взяв
вторую производную
![]() убеждаемся, что эта вторая производная
больше нуля и, следовательно, функция
Э0 = f(h)
имеет минимум, а глубина,
убеждаемся, что эта вторая производная
больше нуля и, следовательно, функция
Э0 = f(h)
имеет минимум, а глубина,
при которой удельная энергия сечения имеет минимум называется критической.
Все элементы потока при глубине равной критической обозначаются с индексом «к». Таким образом в соответствии с уравнением (2.7):
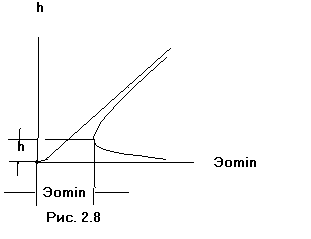
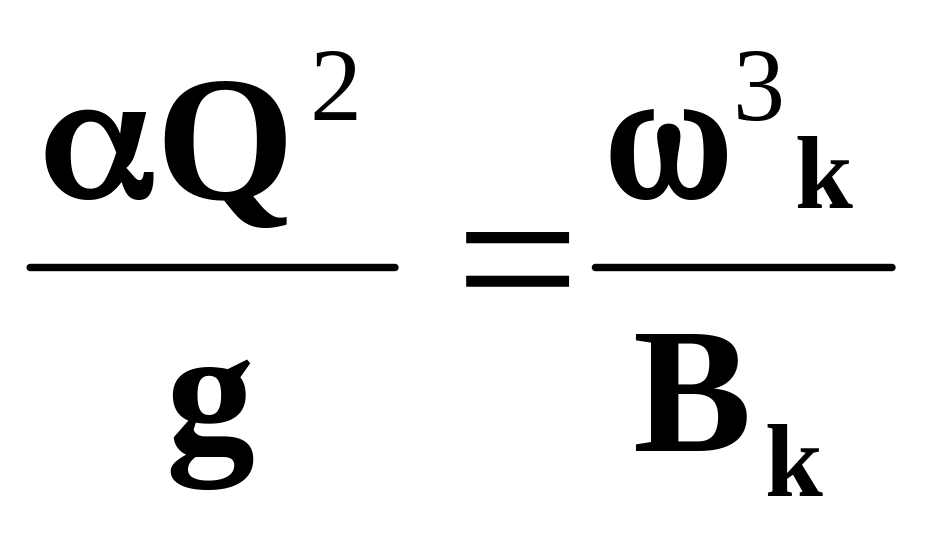 (2.8)
(2.8)
И
 з
рассмотрения рис. 2.8 видно, что второй
асимптотой кривой Э0
=f(h) будет прямая Э0 =
h. Точка кривой,
соответствующая ее минимуму, делит
кривую на две ветви: нижняя отвечает
такому состоянию потока, при котором с
увеличением глубины происходит уменьшение
удельной энергии сечения; верхняя –
соответствует такому состоянию потока,
при котором с увеличением глубины
происходит увеличение удельной энергии
сечения. Очевидно, что одним и тем же
запасом энергии поток обладает при двух
значениях глубин. График на рис 2.8
позволяет определить величину критической
глубины hk,
как глубины, соответствующей минимуму
удельной энергии сечения.
Критическую
глубину можно определить используя
зависимость (2.8). Для этого необходимо
задаться рядом значений h
и подсчитав , В и
3/В построим
кривую 3/В =
f(h), так как
при Э0 min
отношение
з
рассмотрения рис. 2.8 видно, что второй
асимптотой кривой Э0
=f(h) будет прямая Э0 =
h. Точка кривой,
соответствующая ее минимуму, делит
кривую на две ветви: нижняя отвечает
такому состоянию потока, при котором с
увеличением глубины происходит уменьшение
удельной энергии сечения; верхняя –
соответствует такому состоянию потока,
при котором с увеличением глубины
происходит увеличение удельной энергии
сечения. Очевидно, что одним и тем же
запасом энергии поток обладает при двух
значениях глубин. График на рис 2.8
позволяет определить величину критической
глубины hk,
как глубины, соответствующей минимуму
удельной энергии сечения.
Критическую
глубину можно определить используя
зависимость (2.8). Для этого необходимо
задаться рядом значений h
и подсчитав , В и
3/В построим
кривую 3/В =
f(h), так как
при Э0 min
отношение
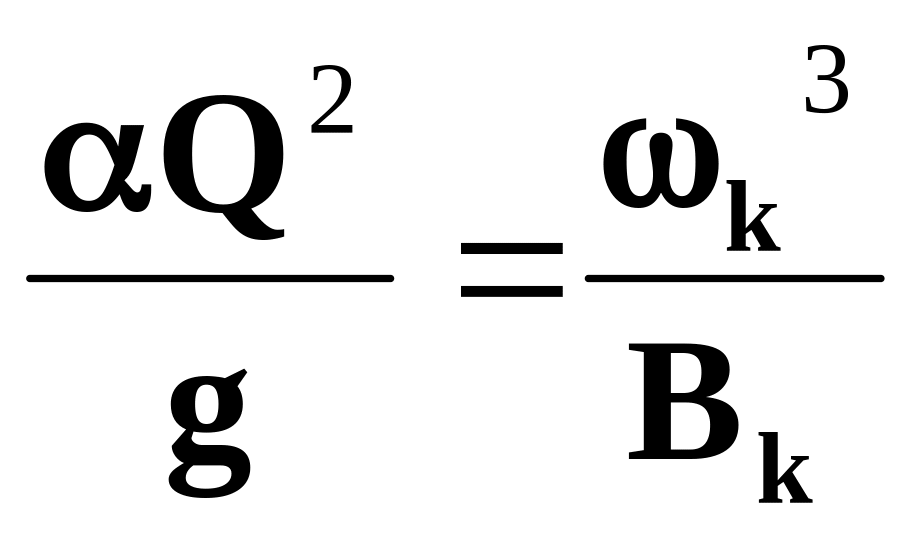 ,то
отложив по оси абсцисс величину
,то
отложив по оси абсцисс величину
![]() ,
получаем кривую
,
получаем кривую
![]() .
Так как при Э0 min
отношение
.
Так как при Э0 min
отношение
 с
праведливо,
то отложив по оси абсцисс величину
, получаем на оси ординат hk
(см. рис 2.9). Уравнение (2.8) не содержит
ни уклона русла, ни его шероховатости,
Следовательно критическая глубина
определяется только расходом русла и
его формой. Для определения критической
глубины можно пользоваться графиком
А.Н.Рахманова.
с
праведливо,
то отложив по оси абсцисс величину
, получаем на оси ординат hk
(см. рис 2.9). Уравнение (2.8) не содержит
ни уклона русла, ни его шероховатости,
Следовательно критическая глубина
определяется только расходом русла и
его формой. Для определения критической
глубины можно пользоваться графиком
А.Н.Рахманова.
При определении hk прямоугольных, треугольных, параболических русел графики не нужны, так как аналитическое определение критической глу
б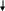 ины
осуществляется
достаточно просто
ины
осуществляется
достаточно просто
1. Прямоугльное русло: вводя в рассмотрение
удельный расход, преобразуем уравнение (2.8)
следующим образом:
![]() (2.9)
(2.9)
При = 1,1 получим: hk = 0,482 q2/3;
При = 1,0 получим hr = 0,467 q2/3;
Так как для прямоугольного русла q = Vk hk, то из формулы (2.9) следует:
![]() а
отсюда следует:
а
отсюда следует:
![]() (2.10)
(2.10)
Для параболическогорусла
![]() при = 1,0
(2.11)
при = 1,0
(2.11)
![]() при = 1,1
(2,12)
при = 1,1
(2,12)
Для треугольного
русла:
![]() при =1,1
(2.13)
при =1,1
(2.13)
Для трапецеидальных русел критическую глубину можно определить, используя метод Агроскина: сначала вычисляем критическую глубину для условного прямоугольного русла:
![]()
г де
Q – расход русла; b
– ширина по дну данного русла. Затем
находим значение величины
де
Q – расход русла; b
– ширина по дну данного русла. Затем
находим значение величины
![]() (2.14)
(2.14)
где m – коэффициент откоса данного русла.
Далее, пользуясь приближенной формулой (2.16) или таблицей находим особое значение функции f(п), после чего вычисляем искомую критическую глубину данного трапецеидального русла:
![]() (2.15)
(2.15)
где:
![]() (2.16)
(2.16)
Критический уклон
Критическим уклоном называется такой уклон призматического русла, при котором для заданного расхода Q и для заданной формы русла нормальная глубина hо равна критической глубине hk. Сделовательно, величина критического уклона может быть определена из формулы Шези.
![]() (2.17)
(2.17)
где ik - критический уклон дна русла.
Подставляя (2.17) в уравнение (2.8) и сокращая на 2 , получим:
![]() откуда
откуда
![]() и так как
и так как
![]()
![]() (2.18)
(2.18)
Для широких и мелких каналов можно считать, что = Bк и тогда:
![]() (2.19)
(2.19)
Введем в рассмотрение критический модуль расхода, то есть модуль расхода при критической глубине, определяемый по формуле:
![]() (2.20)
(2.20)
Тогда уравнение (2.16) перепишется следующим образом:
![]() откуда
откуда
![]() (2.21)
(2.21)
Примечание: положим, что нам заданы
расход Q, форма и размеры
русла, а также его коэффициент шероховатости
n. Определенному уклону
заданного русла будет отвечать вполне
определенная глубина ho.
На рисунке (2. 10) представлено русло,
как бы укрепленное на шарнире О.
Тогда, придавая этому руслу различные
уклоны, будем получать различные глубины
![]()
В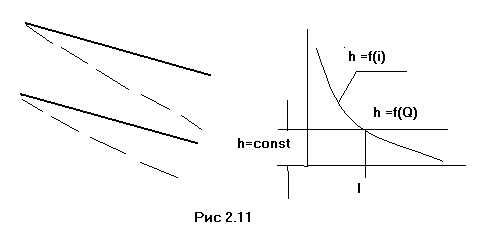 отличие от нормальной глубины критическая
не зависит от уклона дна (для заданного
поперечного сечения), а зависит только
от расхода. Поэтому на графике hk
=f(Q) изображена
прямой, параллельной оси уклонов. Как
видно из этого графика, существует такой
уклон дна i, при котором
имеет место равенство ho=hk.
Этот уклон называется критическим
и обозначается ik.
Очевидно:
отличие от нормальной глубины критическая
не зависит от уклона дна (для заданного
поперечного сечения), а зависит только
от расхода. Поэтому на графике hk
=f(Q) изображена
прямой, параллельной оси уклонов. Как
видно из этого графика, существует такой
уклон дна i, при котором
имеет место равенство ho=hk.
Этот уклон называется критическим
и обозначается ik.
Очевидно:
а) если ik > i, то hk < ho
б) если ik < i, то hk > ho
в) если ik = i, то hk = ho 2.3 Спокойное, бурное и критическое состояние потока.
Выше было установлено, что удельная энергия сечения Э0 будучи непрерывной функцией имеет минимум при критической глубине, причем при этой глубине между гидравлическими элементами живого сечения потока существует зависимость:
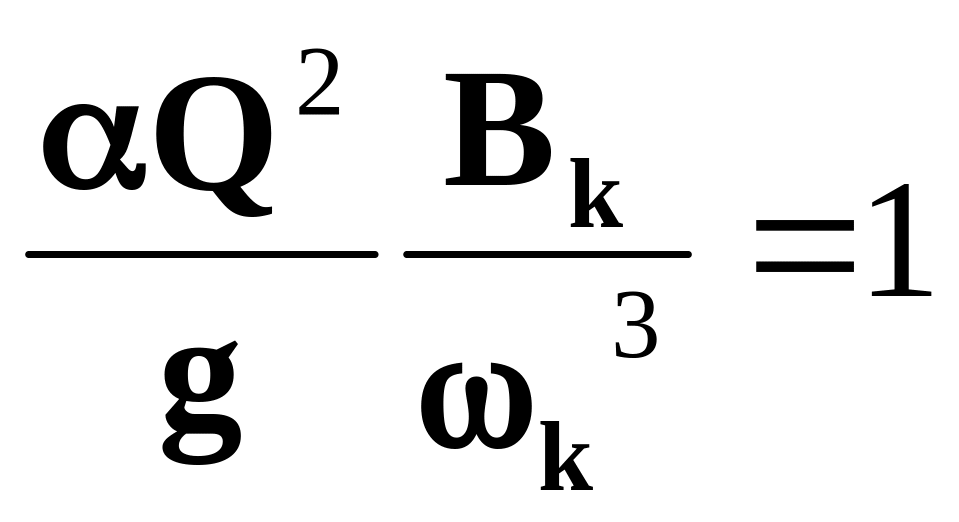 Минимум функции Эо =f
(h), соответствующий
критической глубине и минимуму удельной
энергии сечения, разделяет всю кривую
на две ветви, из которых нижняя
характеризуется уменьшением удельной
энергии сечения с увеличением глубины,
а другая (верхняя) увеличением удельной
энергии сечения с увеличением глубины.
Минимум функции Эо =f
(h), соответствующий
критической глубине и минимуму удельной
энергии сечения, разделяет всю кривую
на две ветви, из которых нижняя
характеризуется уменьшением удельной
энергии сечения с увеличением глубины,
а другая (верхняя) увеличением удельной
энергии сечения с увеличением глубины.
Если при движении потока глубина его
остается меньше критической, то удельная
энергия сечения будет убывающей функцией
глубины, то есть
![]() (нижняя ветвь кривой Эо =
f(h).)
(нижняя ветвь кривой Эо =
f(h).)
Если же при движении воды глубина потока
остается больше критической, то удельная
энергия сечения будет возрастающей
функцией глубины, то есть
![]() (верхняя
ветвь кривой Эо = f(h)
).
(верхняя
ветвь кривой Эо = f(h)
).
Таким образом, критическая глубина
является тем критерием, который разделяет
все потоки на две категории: потоки, для
которых h < hk
и, следовательно
и потоки, для которых h >
hk и,
соответственно,
![]() .
.
Потоки первой категории характеризуются высокими скоростями и малыми глубинами и называются бурными, а потоки второй категории ххарактеризуются малыми скоростями и большими глубинами и называются спокойными. О бурном и спокойном состоянии потока можно говорить и применительно к равномерному движению воды. В этом случае будем иметь: при бурном состоянии потока ho < hk (где ho – нормальная глубина) и i > ik. При спокойном состоянии потока ho < hk и i < ik.
Кроме указанных двух состояний потока может иметь место критическое состояние потока, при котором ho = hk и i = ik. Очевидно, что в последнем случае Эо = Эmin.
Число Фруда
Введем в рассмотрение безразмерный параметр – число Фруда (Fr). Этот параметр является одной из характеристик безнапорного потока.
![]() (2.22)
(2.22)
Здесь V и h - средняя скорость и глубина потока в данном сечении соответственно. Из рассмотрения формулы (2.22) следует, что число Fr можно рассматривать как удвоенное отношение кинетической энергии к потенциальной энергии потока в том же сечении, то есть это отношение является критерием бурности потока.
Имея в виду уравнение(2.10), формулу (2.22) можно переписать так:
![]() (2.23
(2.23
В условиях русла с каким угодно профилем под величиной h в формуле (2.22) нужно подразумевать некоторую среднюю величину hср в данном сечении, определяемую из соотношения:
hср =![]() (2.24)
(2.24)
где и В – площадь
и ширина живого сечения поверху. Тогда
формула (2.22) будет иметь вид:
![]() (2.25)
(2.25)
Если ввести в формулу (2.25) расход потока Q, то получим:
![]() (2.26)
(2.26)
Отсюда следует, что при критической глубине Fr = 1. Таким образом, критерий, определяющий спокойное и бурное состояние потока можно записать в таком виде: Fr > 1 (2.27)
2.3 Основное дифференциальное уравнение установившегося
неравномерного плавноизменяющегося движения воды
Некоторые дополнительные замечания к неравномерному движению воды в открытых руслах
В инженерной практике равномерное движение воды встречается чрезвычайно редко. Оно может иметь место лишь в искусственных водотоках с постоянным по форме и размерам профилем поперечного сечения, однообразной шероховатостью и уклоном дна. В естественных руслах и руслах с гидротехническими сооружениями эти условия никогда не выполняются. Любая преграда, выполненная в русле (плотина, мост и т.д.), любые неровности дна, изменение уклона вызывают неравномерное движение воды. Искусственные сооружения, возводимые на каналах всегда сопровождаются такими участками канала (переходами), где равномерное движение воды с физической точки зрения просто невозможно (русло с переменной шириной по дну, с горизонтальным дном, с обратным уклоном дна и т.д.)
П усть живое сечение потока стеснено устоями моста. Для того, чтобы уменьшенное сечение потока могло пропустить заданный расход, средняя скорость в пределах сооружения должна увеличиваться, что, в свою очередь должно потребовать некоторого повышения свободной поверхности потока и, следовательно, уменьшения скорости течения перед мостом. Таким образом, перед мостом будет наблюдаться замедленное движение потока, которое переходит затем в ускоренное, а после моста снова становится замедленным. Равномерное движение характеризуется неизменностью гидравлических элементов по длине потока и, с позиций механики требует равновесия всех сил, действующих на какой-либо элемент потока, так как при равномерном движении живая сила остается постоянной по длине потока, а работа сил трения на данном перемещении должна быть равна работе остальных действующих сил на соответствующих перемещениях.
При неравномерном движении наблюдается или изменение средней скорости потока или перераспределение скоростей по живому сечению потока, что обуславливает появление сил инерции и нарушает равновесие сил.
С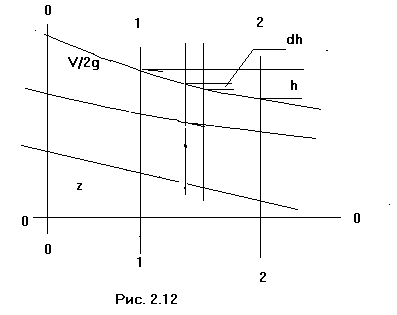

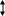


 тремление
многочисленных исследователей описать
математически неравномерное движение
привело к выводу основного уравнение
неравномерного плавноизменяющегося
движения воды в открытых руслах,
основанному на уравнении Бернулли.
Запишем уравнение Бернулли для двух
сечений, расположенных на расстоянии
ds друг от друга (рис. 2.12):
тремление
многочисленных исследователей описать
математически неравномерное движение
привело к выводу основного уравнение
неравномерного плавноизменяющегося
движения воды в открытых руслах,
основанному на уравнении Бернулли.
Запишем уравнение Бернулли для двух
сечений, расположенных на расстоянии
ds друг от друга (рис. 2.12):
![]() (2.28)
(2.28)
Здесь ро – давление на свободной поверхности потока.
dh - член, учитывающий
потери напора на преодоление гидравлического
сопротивления между сечениями, для
которых записано уравнение Бернулли.
После сокращений уравнение (2.28) примет
вид
![]() или, пренебрегая бесконечно малой
величиной второго порядка, получим:
или, пренебрегая бесконечно малой
величиной второго порядка, получим:
![]() (2.29)
(2.29)
Обозначим
![]() ,
тогда –dz=dhv+dh
(2.30)
,
тогда –dz=dhv+dh
(2.30)
Потери напора складываются из потерь напора на трение и потерь напора на преодоление местных сопротивлений: dh = dhм + dhтр и уравнение (2.30 может быть представлено в следующем виде:
- dz = dhv + dhм + dhтр (2.31)
Следует заметить: что потери напора на преодоление местных сопротивлений обусловлены изменением живого сечения по длине потока. Но так как изменение живого сечения в искусственных руслах осуществляется весьма медленно, то потери напора на преодоление местных сопротивлений по сравнению с потерями напора на трение весьма малы и ими чаще всего пренебрегают. Полагая в уравнении (2.31) dhм = 0, получаем более простое уравнение, которое обычно и применяется при рассмотрении неравномерного движения воды в открытых руслах.
- dz = dhv + dhтр (2.32)
Приведем это уравнение к виду, удобному для расчетов, для чего разделим обе его части на ds:
![]() (2.33)
(2.33)
г
де
![]() -
пьезометрический уклон (уклон свободной
поверхности в данном сечении). Знак (-)
означает, что понижению свободной
поверхности потока, то есть уменьшению
координаты z соответствует
положительное значение пьезометрического
уклона.
-
пьезометрический уклон (уклон свободной
поверхности в данном сечении). Знак (-)
означает, что понижению свободной
поверхности потока, то есть уменьшению
координаты z соответствует
положительное значение пьезометрического
уклона.
![]() = if
- гидравлический уклон, то есть потери
напора на единицу длины потока:
= if
- гидравлический уклон, то есть потери
напора на единицу длины потока:
![]() (2.34)
(2.34)
При этом необходимо заметить, что в отличие от равномерного движения гидравлические элементы потока V, C, R здесь переменные по длине потока. Тогда уравнение (2.33) с учетом (2.29) и (2.34) можно записать в следующем виде:
![]() (2.35)
(2.35)
Заменив скорость V расходом
Q, учитывая, что
![]() ,
получим:
,
получим:
![]() ,
то
,
то
![]() (2.36)
(2.36)
где К – модуль расхода.
Таким образом основное дифференциальное уравнение неравномерного плавноизменяющегося движение воды в открытых руслах можно записать либо в форме (2.35) либо в форме (2.36). Преобразуем последнее уравнение, введя в него глубину потока h. Пусть расход потока задан. Кроме того, будем считать заданной форму русла, так что все гидравлические элементы потока (w, c, R…) будем рассматривать, как непрерывные функции глубины потока h. Сначала установим связь между пьезометрическим уклоном I, глубиной потока h и уклоном дна русла i в данном сечении. Из рассмотрения рисунка 2.13 видно, что для произвольно выбранного сечения х-х, отстоящего от начального сечения О-О на расстоянии S, можно написать:
z = a + h – is (2.37)
|
Дифференцируя (2.37) по s, получим:
так
как
Эта зависимость играет важное значение при изучении неравномерного двжения воды в открытых руслах.
|
При равномерном движении глубина вдоль потока остается постоянной, то есть
 и I = i
– уклон свободной поверхности
(пьезометрический уклон) равен уклону
дна.
и I = i
– уклон свободной поверхности
(пьезометрический уклон) равен уклону
дна.При кривой подпора глубина вниз по течению повышается, то есть
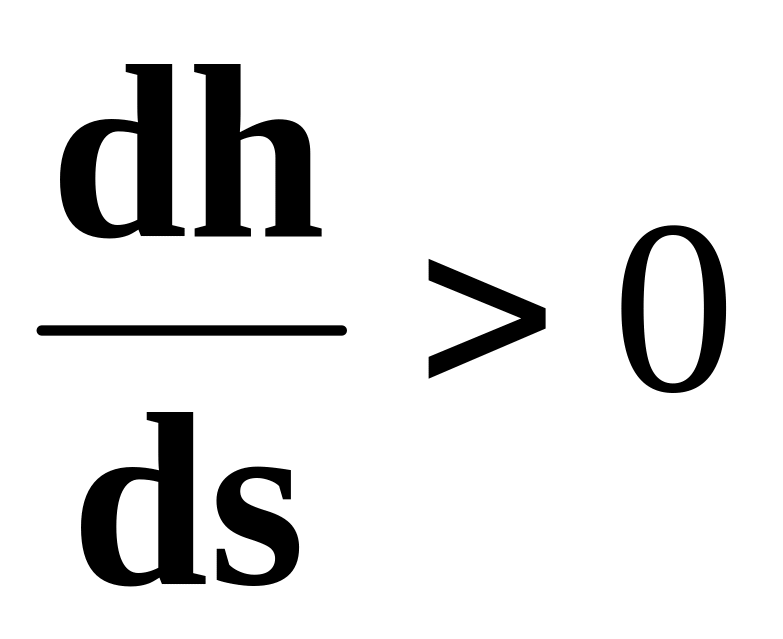 -
величина положительная, в силу чего I
< i, то есть уклон
свободной поверхности меньше уклона
дна.
-
величина положительная, в силу чего I
< i, то есть уклон
свободной поверхности меньше уклона
дна.При кривой спада глубина вниз по течению уменьшается
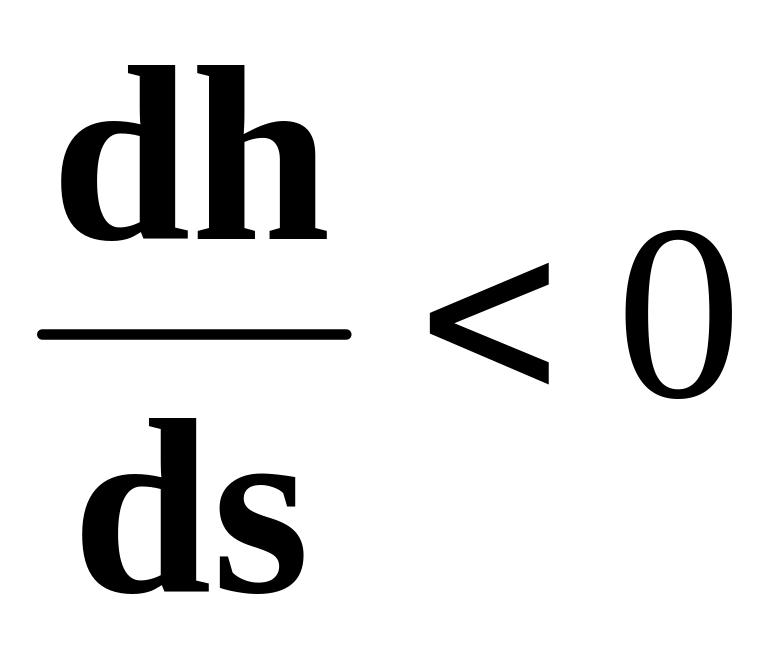 - величина отрицательная, вследствие
чего I > i,
- величина отрицательная, вследствие
чего I > i,
Выполним дифференцирование правой части уравнения (2.36):, предполагая, что русло является непризматическим, то есть w = f (h, s)
![]() Учитывая, что
Учитывая, что
![]() ,
получим:
,
получим:
![]() (2.40)
(2.40)
Принимая во внимание уравнение (2.40), уравнение (2.36) запишется так:
![]() (2.41)
(2.41)
В случае равномерного движения
![]() и
тогда
и
тогда
![]() то есть уравнение (2.41) обращается в
уравнение равномерного движения.
то есть уравнение (2.41) обращается в
уравнение равномерного движения.
Решим уравнение (2.41) относительно
![]() :
:
![]() откуда:
откуда:
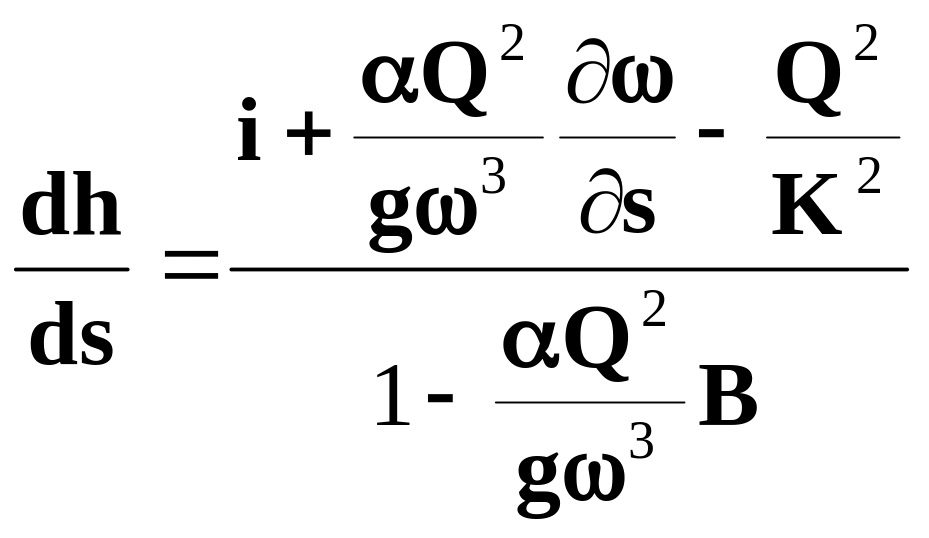 (2.42)
(2.42)
С учетом того, что K2 = w2C 2 R, уравнение (2.42) примет вид:
 (2.43)
(2.43)
Уравнение (2.43) и является уравнением неравномерного плавноизменяющегося движения воды в открытых руслах, определяющее зависимость глубины потока от расстояния от начального сечения.
Вид дифференциального уравнения неравномерного плавноизменящего-
ся движения воды в случае призматического русла.
Для призматического русла, то есть русла
геометрические размеры которого
постоянны и не изменяются по длине
![]()
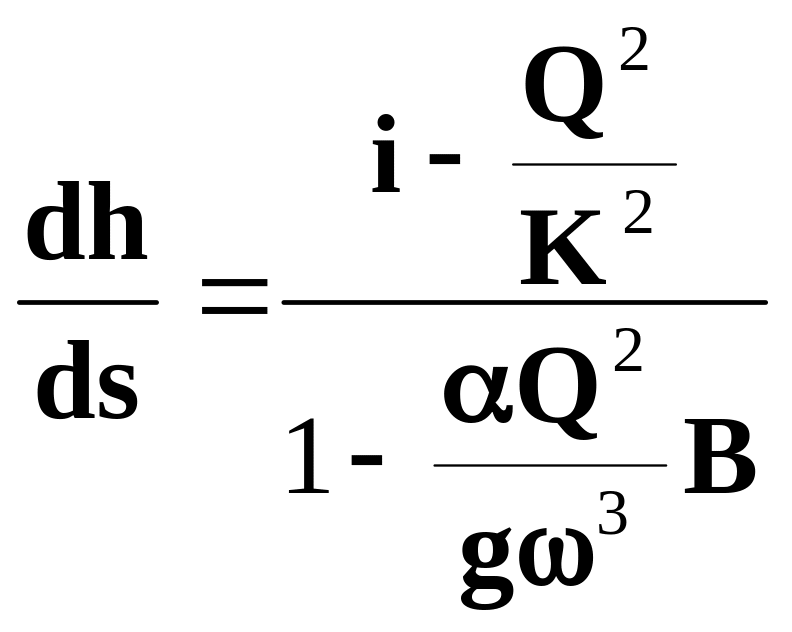 (2.44)
(2.44)
Уравнение (2.44) является основным уравнением неравномерного плавноизменяющегося движения воды в призматических руслах с прямым уклоном дна.
2.4 Преобразование основного уравнения неравномерного движения воды
к виду, удобному для анализа
При анализе основного уравнения неравномерного движения воды в открытых руслах можно различать три случая: 1. i > 0; 2. i = 0; i < 0.
Русло с прямым уклоном дна (i > 0). Для этого случая уравнение получено в виде: . Введем в рассмотрение вспомогательный поток с равномерным движение. Причем расход этого потока при заданной форме поперечного сечения русла, при заданном уклоне дна равен расходу Q, наблюдающемуся при неравномерном движении. Расход этого вспомогательного потока можно выразить известной зависимостью:
![]()
где Ко- модуль расхода, отвечающий нормальной глубине hо. Теперь основное уравнение неравномерного движения можно представить в следующем виде:
Числитель этого уравнения:
![]() (2.45)
(2.45)
Преобразуем знаменатель правой части уравнения (2.44):
![]() (то есть мы умножили числитель и
знаменатель дроби на С2R).
Учитывая, что К2 = w2С2R
и w = Rc,
получим:
(то есть мы умножили числитель и
знаменатель дроби на С2R).
Учитывая, что К2 = w2С2R
и w = Rc,
получим:
![]() (2.46)
(2.46)
где j =
![]() ;
В соответствии с выражениями (2.45) и
(2.46) представим уравнение (2.44) в следующем
виде:
;
В соответствии с выражениями (2.45) и
(2.46) представим уравнение (2.44) в следующем
виде:
 (2.47)
(2.47)
Используя показательный закон, запишем уравнение (2.47) в следующем виде:
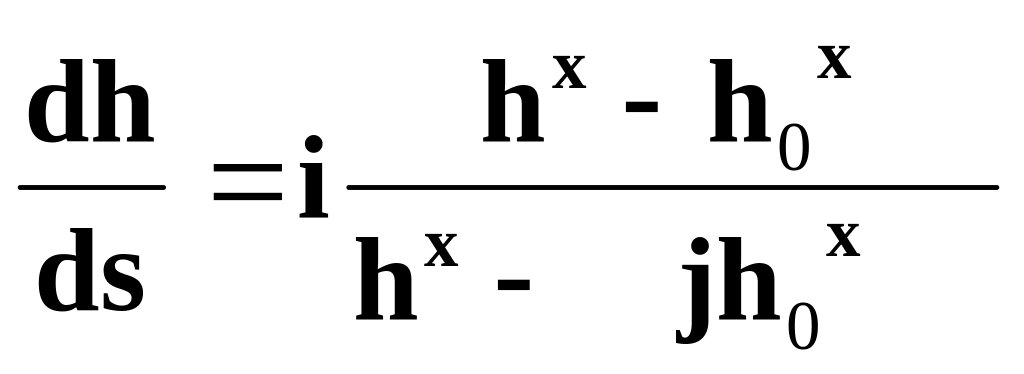 (2.48)
(2.48)
Учитывая, что при h = hk hkx - hоx = 0, hох = hk. Тогда:
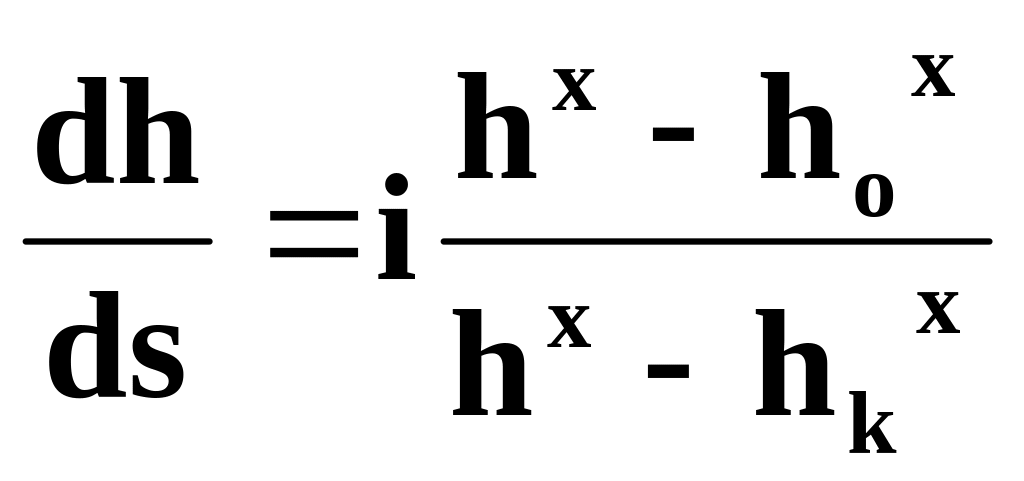 (2.49)
(2.49)
Русло с горизонтальным дном
Если призматическое русло имеет горизонтальное дно, основное уравнение неравномерного движения запишется следующим образом:
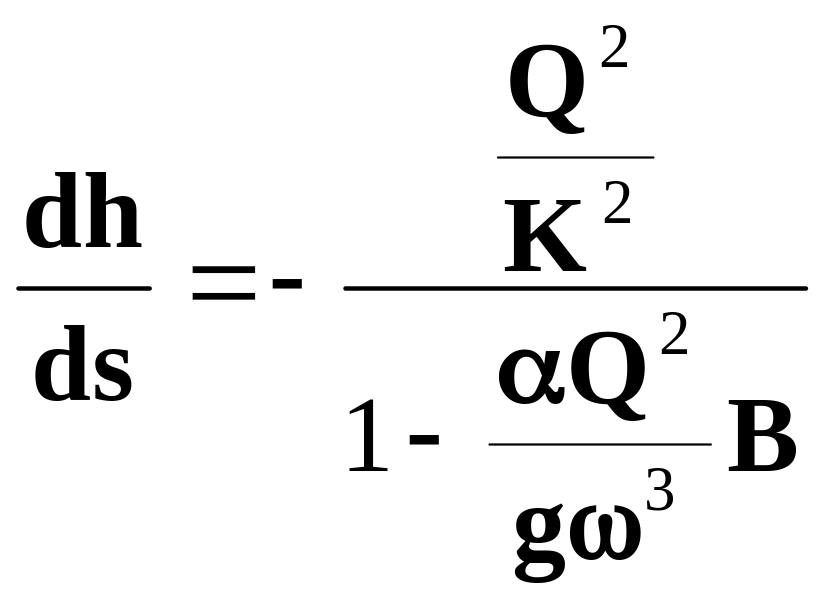 (2.50)
(2.50)
Здесь также вводим в рассмотрение поток с равномерным движением и глубиной, равной критической и, следовательно, расход вспомогательного потока равен:
Q
= K k![]() (2.51)
(2.51)
Тогда:
 = -
= -
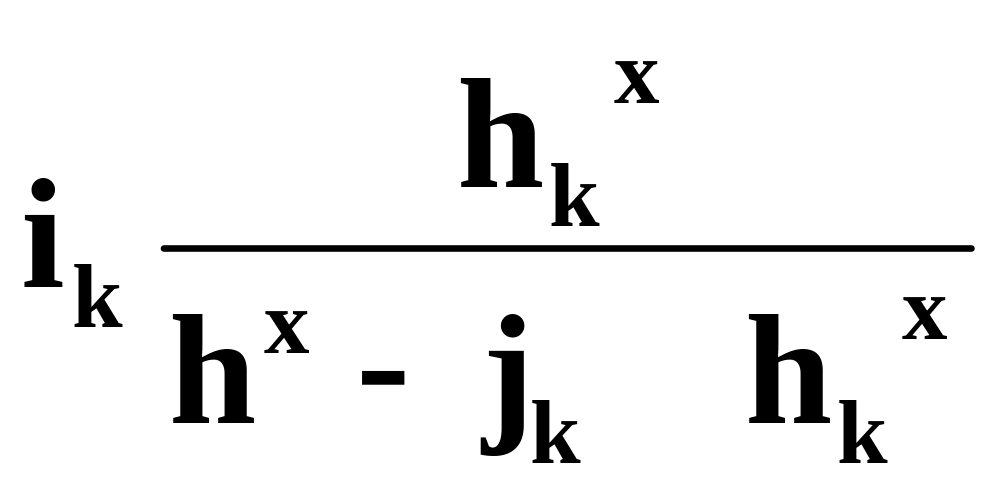 (2.52)
(2.52)
Учитывая, что при h = hk hx - hkx = 0, уравнение (2.52) запишется:
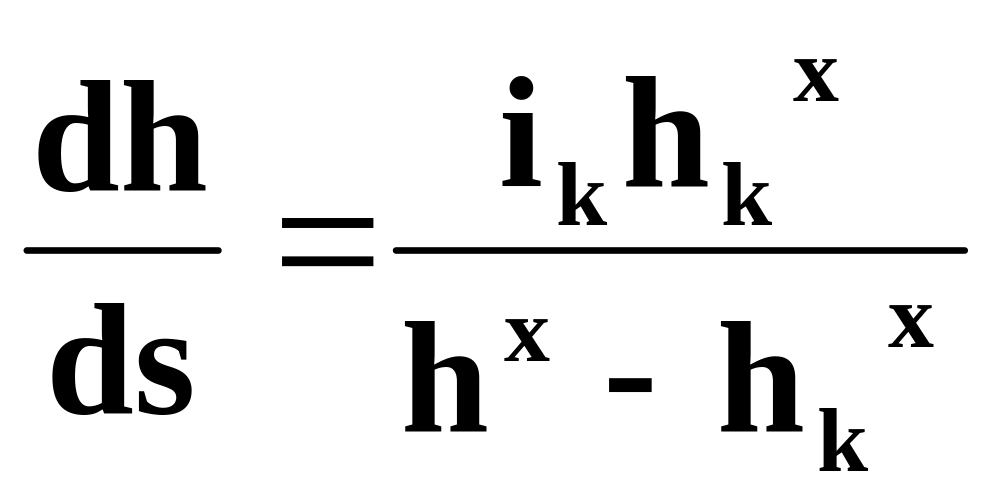 (2.53)
(2.53)
Русло с обратным уклоном
В этом случае дифференциальное уравнение
неравномерного движения воды в открытых
руслах примет вид: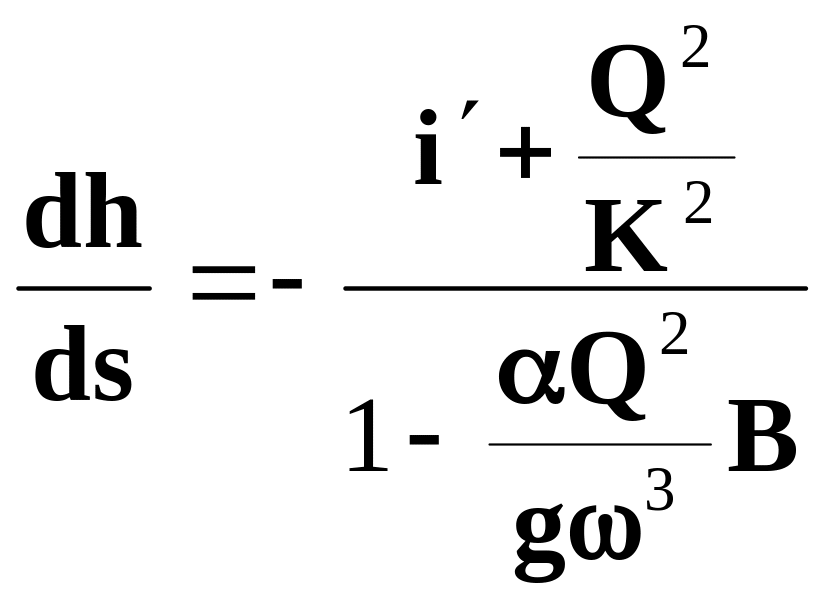 (2.54)
(2.54)
Введем в рассмотрение вспомогательный
поток с равномерным движением, причем
нормальную глубину
![]() этого потока, отвечающую расходу Q
при неравномерном движении в русле с
заданной формой поперечного сечения,
определим в предположении, что вода
течет в обратном направлении. Тогда.
Очевидно, будет:
этого потока, отвечающую расходу Q
при неравномерном движении в русле с
заданной формой поперечного сечения,
определим в предположении, что вода
течет в обратном направлении. Тогда.
Очевидно, будет:
![]() (2.55)
(2.55)
где
![]() модуль расхода при глубине
модуль расхода при глубине
![]() .
При условии (2.55) уравнение (2.54) запишется
так:
.
При условии (2.55) уравнение (2.54) запишется
так:
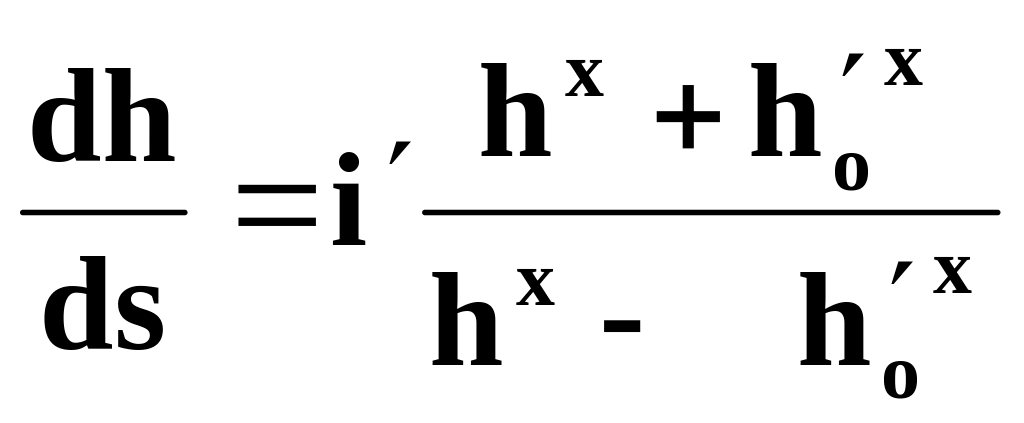 (2.56)
(2.56)
Возможные случаи соотношений между глубиной неравномерного движения h, нормальной глубиной hо и критической глубиной.
Каналы с прямым уклоном дна:
1. при i < ik, h > hk.
а) h > hо > hk
б) hо > h > hk
в) hо > hk > h
2. при iо > ik, hо < hk
а) h > hk > hо
б) hk > h > hо
в) hk > hо > h
при iо = ik, hо = hk возможны лишь два соотношения:
а) h > hk
б) h < hk
Если дно канала горизонтальное или имеет обратный уклон возможны лишь два соотношения:
а) h > hk
б) h < hk.
2.5. Исследование форм свободной поверхности потока в случае неравномерного плавноизменяющегося движения воды в призматических руслах.
Русло с прямым уклоном дна i > 0:
Выше мы получили уравнение (2.52)
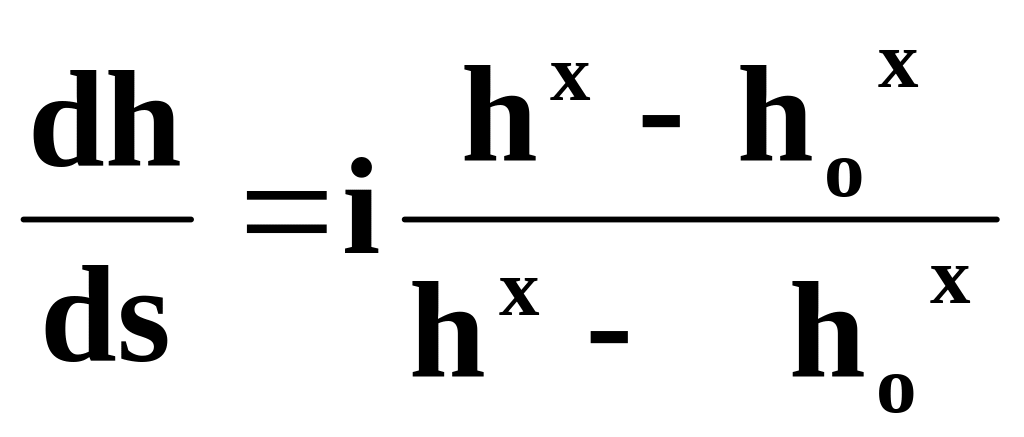 учитывая, что знаменатель правой части
ётого уравнения при h = hk
должен обращаться в нуль, можем записать:
учитывая, что знаменатель правой части
ётого уравнения при h = hk
должен обращаться в нуль, можем записать:
![]() ,
откуда, допуская, что величина = const,
получаем:
,
откуда, допуская, что величина = const,
получаем:
![]()
То есть мы получили уравнение (2.53)
 Это уравнение используем для анализа
кривых свободной поверхности при прямом
уклоне дна. Здесь различают три случая:
Это уравнение используем для анализа
кривых свободной поверхности при прямом
уклоне дна. Здесь различают три случая:
а) hо > hk; i < ik;
б) hо < hk; i > ik;
в) hо = hk; i = ik.
Рассмотрим, каковы будут кривые свободной поверхности в каждом из этих случаев. Случай а): представим себе продольный профиль заданного русла. Линии NN и КК разбивают всю область потока по высоте на три отдельные зоны а, b, c (рис. 2.14). В этом случае возможны три различные формы кривой свободной поверхности: кривая а1, когда h > hо > hk. Как видно, здесь мы имеем свободную поверхность, лежащую в зоне а выше линии NN. При этом получаем числитель и знаменатель уравнения (2.53) положительными. Следовательно . Отсюда заключаем, что глубина потока вниз по течению должна увеличиваться, следовательно кривая а1 является кривой подпора. В практике такая кривая свободной по-
|
верхности может появиться, например, после устройства плотины. Докажем теперь, что кривая а1 имеет две асимптоты: в верховой своей части линию NN и в низовой – горизонтальную прямую АB. При стремлении h к hо (см. левый конец кривой а1) стремится к нулю, следовательно в
|
верховой своей части кривая а1 асимптотически приближается к линии NN, характеризуемой условием . Вниз по течению глубины увеличиваются; при стремлении h к бесконечности стремится к i:
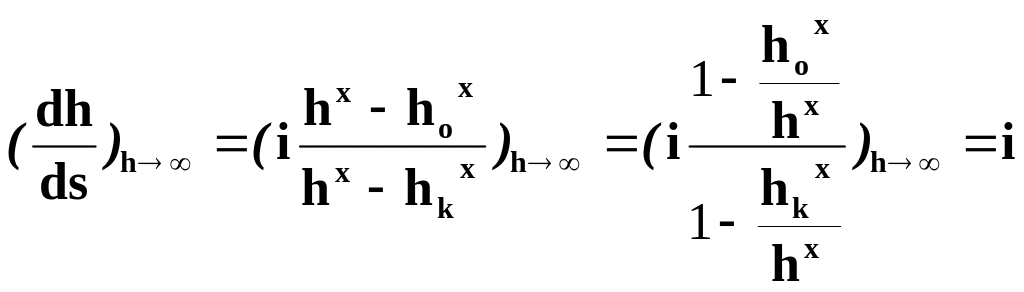 (2.57)
(2.57)
О


 тсюда
заключаем, что в низовой части кривая
имеет горизонтальную асимптоту.
Действительно горизонтальная прямая
АВ (рис. 2.14) характеризуется условием
тсюда
заключаем, что в низовой части кривая
имеет горизонтальную асимптоту.
Действительно горизонтальная прямая
АВ (рис. 2.14) характеризуется условием
![]() А В
А В
 ds
dh
ds
dh
Рис.2.15
Учитывая, что кривая а1 имеет
две асимптоты в виде линий NN
и AB, можно утверждать, что
выпуклость этой кривой направлена вниз.
Так как кривая а1асимптотически
приближается к прямой NN,
то ясно, что подпор, вызванный плотиной
или другим подпорным сооружением
распространяется вверх по течению,
теоретически на бесконечную длину.
Однако на практике пренебрегают некоторой
незначительной величиной
![]() (рис.2.15), равной (0,01-0,02)hо
и считают длину кривой подпора так
как показано на рисунке.
(рис.2.15), равной (0,01-0,02)hо
и считают длину кривой подпора так
как показано на рисунке.
Кривая b1: |
Здесь свободная поверхность потока
лежит в зоне b (рис. 2.13).
Так как hо>h>hk,
то правая часть уравнения (2.49) получается
отрицательной (dh/ds<0),
то естькривая свободной поверхности
является кривой спада. Поскольку при
стремлении h к hо
кривая асимптотически приближается к
линии нормальных глубин NN,
а при стремлении h к hk
получаем
![]() ,
то заключаем, что кривая b1
будет иметь вид, показанный на рисунке
2.13. Выпуклость этой кривой направлена
вверх. Слева эта кривая имеет асимптотой
линию NN, справа вертикальную
касательную,
,
то заключаем, что кривая b1
будет иметь вид, показанный на рисунке
2.13. Выпуклость этой кривой направлена
вверх. Слева эта кривая имеет асимптотой
линию NN, справа вертикальную
касательную,
Кривая с1 (рис 2.13) находится в зоне с. Так как h < hk < hо, то правая чаять этого уравнения оказывается положительной ( ) иБ следовательно, кривая с1 является кривой подпора. Кривая с1 асимптот не имеет; к линии КК она подходит, имея вертикальную касательную. Выпуклость кривой направлена вниз.
Случай б) hо < hk и iо > ik. Исследование уравнения (2.53) показывает, что здесь, как в в случае а), возможны три вида кривых свободной поверхности.
Кривая а2, когда h
> hk
> hо. Эта кривая
лежит в зоне а (выше линии КК),
,
следовательно глубина вниз по течению
увеличивается, то есть кривая а2
является кривой подпора. Вниз по течению
(при
![]() )
а2 асимптотически приближается
к горизонтальной прямой: к линии КК
(при
)
а2 асимптотически приближается
к горизонтальной прямой: к линии КК
(при
![]() )
она подходит, имея вертикальную
касательную. Очевидно, что кривая а2
имеет выпуклость, направленную вверх.
Эта кривая может появиться, например,
после устройства преграды в русле,
имеющем большой уклон (рис. 2.17)
)
она подходит, имея вертикальную
касательную. Очевидно, что кривая а2
имеет выпуклость, направленную вверх.
Эта кривая может появиться, например,
после устройства преграды в русле,
имеющем большой уклон (рис. 2.17)
|
Кривая b2 при h>hk>hо Эта кривая Лежит в зоне b. Исследуя уравнение (2.49) видим, что в данном случае , следовательно, в этом случае глубины потока вниз по течению уменьшаются. Так как к линии КК рассматриваемая кривая подходит, имея вертикальную касательную WW, а к линии NN эта кривая подходит |
асимптотически, то заключаем, что кривая b2 должна быть обращена выпуклостью вниз.
Кривая с2, когда h<hо<hk
Кривая лежит в зоне с. Исследование уравнения (2.49) показывает, что и, следовательно кривая с2 является кривой подпора. Она имеет асимптоту NN (рис.2.18)
|
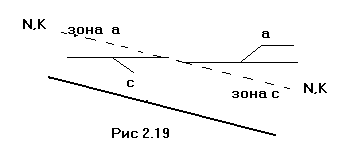
Случай в) hо= hk; i = ik. Здесь линии NN и КК совпадают (рис 2.19) и поэтому зона b исчезает. Остаются только зоны а и c. В соответствии с этим получаем две кривые: а3 и с3. Уравнение (2.49) принимает вид:
|
|
|
Случай i = 0. В
случае горизонтального русла равномерное
движение невозможно и понятие нормальной
глубины теряет смысл. В этом случае
![]() и
поэтому зона а исчезает (линия NN
располагается на бесконечно большом
расстоянии от линии дна); остаются только
зоны b и с.
Следовательно при i = 0
возможны только две кривые (рис 2.20):
кривая спада b0,
лежащая в зоне b,
когда h>hk
и кривая подпора с0, лежащая
в зоне с, когда h<hk
и
поэтому зона а исчезает (линия NN
располагается на бесконечно большом
расстоянии от линии дна); остаются только
зоны b и с.
Следовательно при i = 0
возможны только две кривые (рис 2.20):
кривая спада b0,
лежащая в зоне b,
когда h>hk
и кривая подпора с0, лежащая
в зоне с, когда h<hk
П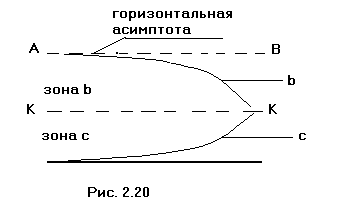 римечание:
при построении кривых свободной
поверхности следует руководствоваться
следующим правилом: кривая свободной
поверхности к линии нормальных глубин
всегда подходит асимптотически, никогда
не пересекая ее а к линии критических
глубин подходит, имея вертикальную
касательную.
римечание:
при построении кривых свободной
поверхности следует руководствоваться
следующим правилом: кривая свободной
поверхности к линии нормальных глубин
всегда подходит асимптотически, никогда
не пересекая ее а к линии критических
глубин подходит, имея вертикальную
касательную.




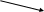
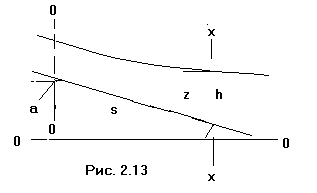
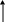
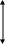


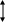
 Рис 2.18
Рис 2.18