Если в выражение для гидравлического радиуса

подставить значение , то получим:

(1.23)

Все гидравлические элементы потока можно выразить через относительную ширину по дну:

 = h(b + mh) = h(h + mh) = h (1.24)

= h + 2h = h( ) (1.25)

= (1.26)

Для того, чтобы записать эти выражения для гидравлически наивыгоднейшего профиля, необходимо подставить в них значение .

1.5. Основные типы задач по гидравлическому расчету каналов

Трапецеидальный канал характеризуется следующими шестью величинами: b, h, m, определяющие гидравлические элементы потока и n, i, Q. Некоторые из приведенных величин заданы условиями проектирования.

1.Задачи, в которых задано живое сечение, то есть в число заданных величин входят b, m, h . Эти задачи решаются непосредственно без подбора искомой величины. Метод решения:

Заданы b, m, h, n, i. Требуется определить пропускную способность канала Q

Решение:

а) Определяем  и :  = h(b + mh);  = b + 2h

б) Находим гидравлический радиус: R =

в) Определяем коэффициент Шези по формуле Павловского:

г) Определяем пропускную способность канала:

Если неизвестен гидравлический уклон при известных b, m, h, n, Q, задача решается следующим образом: а) находим, как и в предыдущем случае , , R, C;

б) определяем среднюю скорость V: V = ;

в) Находим i: или

2. Задачи, в которых живое сечение не задано, то есть в число искомых величин входят b или h. Задачи этой группы всегда решаются методом подбора искомой величины:

Заданы: m, b, n, i, Q. Требуется найти глубину наполнения канала.

Решение: составляем таблицу, в которой задаемся рядом значений h и для каждого значения h вычисляем расход канал а Q

Т-ца 1.1

Наименование величин И расчетные формулы	Размер- ность	Задаваемые и необходимые Численные значения					Примеча- ния
h	м	h h h h h
mh	м	…	…	…	…	…
b+ mh	м	…	…	…	…	…
 = h(b + mh)		…	…	…	…	…
)	м	…	…	….	….	…
R = /	м	….	….	….	….	….
		….	….	….	….	….
K = C		….	….	….	….	….
Q = K		….	….	….	….	….

По данным первой и последней строк таблицы строим график: (h):

h

Q = (h)

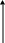Q

Рис 1-3

По этому графику, зная заданный расход Q, находим искомую глубину h, которую называют нормальной глубиной и обозначают .

В том случае, когда заданы m, h, i, n, Q и требуется определить b, задача решается аналогичным способом.

3. Задачи, в которых в число заданных величин входит средняя скорость

Заданы: m, b, h, (то есть задано живое сечение) n, i. Требуется найти Q и i.

Решение: а) Вычисляем площадь живого сечения

 = h(b + mh)

б) Определяем расход Q

Q = v 

в) Определяем уклон i

Здесь C и R могут быть определены предварительно.

Заданы: m, n, Q, v и одна из величин h или b. Требуется найти уклон i и величину b или h.

Решение: а) площадь живого сечения

б) Учитывая, что , находим недостающий размер сечения. в) Уклон определяем по формуле

Заданы: m, n, Q, i, v. Требуется найти b и h.

Решение: Определяем площадь сечения  и модуль скорости W. Обозначем:

Записываем систему двух уравнений с двумя неизвестными:

(b,h)

= (b,h)

h(b+mh=A; = B

Где А и B – известные числа.

Искомые величины находим, решая указанную систему.

1.6 Показательный закон

Исследования по расчету каналов показали, что квадраты расходных характеристик К для данного сечения канала относятся как соответствующие им глубины в некоторой степени х:

(1.27)

при этом величина х зависит от формы сечения канала. Приведенное отношение названо академиком Павловским показательным законом. Показательный закон не является абсолютно точной зависимостью, но дает удовлетворительные результаты при решении практических задач.

Пользуясь выражением (27), можно определить гидравлический показатель русла:

(1.28)

Из выражения (27) следует:

откуда = (1.29)

Определив для заданного сечения канала гидравлический показатель русла х и использовав для одной из глубин h величину К, находят величину расходной характеристики , соответствующую нормальной глубине:

(1.30)

1.7 Ограничение скоростей движения воды в каналах

Большие скорости движения воды в каналах опасны тем, что они приводят к размыванию дна и откосов канала. Поэтому чем больше скорость тем надежнее должно быть крепление земляного канала во избежание его размыва. Наоборот, малые скорости при наличии в воде примесей в виде песка или более мелких частиц приводят к заилению каналов, что вызывает необходимость в дорогостоящей очистке. Следовательно, необходимо, чтобы скорость движения воды в каналах находилась в пределах:

(1.31)

где так называемая, максимально допустимая средняя скорость при равномерном движении воды. Эту скорость называют максимальной неразмывающей скоростью.

минимально допустимая средняя скорость при равномерном движении воды в канале. Эту скорость называют критической или незаиляющей скоростью.

Действительная скорость V зависит от уклона канала. Максимальная допустимая средняя скорость не зависит от уклона канала, а только от рода материала из которого выполнены стенки, образующие канал и в некоторых случаях от глубины воды в канале.

Для каналов, проложенных в несвязных грунтах (песчаных, гравелистых, галечно-песчаных и др.) проф. И.И.Леви предложил формулу:

(1.32)

где А – коэффициент, зависящий от уплотнения грунта русла канала. Величина этого коэффициента может приниматься равной 1,4 для хорошо уплотненных грунтов и 1,2 для грунтов с более рыхлой структурой.

средняя крупность зерен грунта канала, м.

R - гидравлический радиус потока, м.

При скорости большей допустимой максимальной вертикальные пульсационные скорости становятся столь значительными, что поверхностные частицы грунта (образующего русло канала) оторвавшись от дна, поддерживаются во взвешенном состоянии. В нижеследующей таблице 1.2 приведены приближенные значения , которые относятся как к грунтам, так и к некоторым покрытиям, используемым для защиты каналов от размыва. Эти данные относятся к прямолинейным (в плане) каналам. Для извилистых (в плане) каналов рекомендуется снижать на 5-20%.

Таблица 1.2

Максимально допустимые скорости при равномерном движении воды

Материал смоченной поверх- ности канала	, м/с	Материал смоченной поверх- ности канала	, м/с
Несвязные грунты		Скальные породы
Пыль, ил	0,15 – 0,20	Осадочные	2,5 – 4,5
песок	0,20 – 0,60	Кристаллические	20 - 25
гравий	0,60 - 1,20	Крепления
Связные грунты		Одиночная мостовая	3,0 – 3,5
Супесь и суглинок	0,7 – 1,0	Двойная мостовая	3,5 – 4,5
глина	1,0 - 1,8	Бетонная облицовка	5,0 – 10,0

Минимальная допускаемая (минимальная незаиляющая) скорость V_min может быть определена для каждого конкретного случая по одной из имеющихся в справочниках эмпирических формул, например:

(1.33)

где е – коэффициент, учитывающий количество взвесей, их гранулометрический состав и шероховатость русла. При n = 0,0225 и среднем диаметре преобладающей массы взвешенных частиц не более 0,25 мм величину коэффициента е можно принимать равной 0,5.

Если условие V > V_min выдержать не удается, приходится предусматривать периодическую очистку канала от отложений.

Условие V< V_max должно быть всегда выдержано, так как в противном случае канал будет разрушаться.

В том случае, когда на первом этапе расчета получаем V>V_max приходится предусматривать мероприятия, позволяющие либо увеличить скорость V_max, либо уменьшить скорость V и в результате добиться соотношения V<V_max.

Мероприятия по увеличению скорости V_max.

Для увеличения максимально допустимой скорости движения воды в русле необходимо применять, например, покрытие откосов и дна канала каким-либо креплением в виде каменной мостовой, бетонной облицовки и т. д. Предусмотрев такое крепление мы, естественно, увеличим скорость V_max

Мероприятия по уменьшению скорости V

Скорость V = и, следовательно, для того чтобы уменьшить скорость V необходимо уменьшить либо С, либо R, либо i. Поэтому применяют для уменьшения скорости V применяют три разных приема:

а) Создание искусственной шероховатости, что приводит к увеличению коэффициента шероховатости n и, следовательно снижению численного значения коэффициента Шези C . Этот прием в случае достаточно длинных каналов неприемлем с экономической точки зрения.

б) Изменение формы поперечного сечения канала с целью уменьшения гидравлического радиуса R. Однако за счет изменения R не удается ощутимо изменить скорость.

в) Наиболее распространенным приемом является является уменьшение уклона дна канала, для чего по длине канала устраиваются перепады

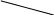
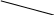
V>V_max

А i,L V=V_max

D i L

С B

L

Рис 1-4

Стремясь получить минимальный объем земляных работ линию дна AB канала назначают, примерно, параллельно поверхности земли и, следовательно на первом этапе расчета уклон дна канала i назначают равным уклону поверхности земли. Если приняв этот уклон и выполнив гидравлический расчет получим: V>V_max, то в этом случае устраивается перепад AD. При этом уклон уменьшается до значения, удовлетворяющее условию: V=V_max

Из рис. 1-4 видно, что высота перепада AD равна:

AD = AC-DC = i L – i L

Где L и L – длины канала.

Так как уклоны каналов малы, то можно считать, что L = L= L₀

где L₀ – длина горизонтальной проекции дна канала.

Учитывая это, можно записать: AD = (i –i ) L₀ (1.34)

Если величина AD получается большой (> 2-3 м), то по длине канала устраиваются несколько перепадов. Перепады устраиваются в виде подпорных стен.

При проектировании каналов для чистой воды, не несущей осаждающихся примесей все же необходимо принимать скорость движения воды не менее 0,2-0,25 м/с, учитывая, что канал создает большую водную поверхность, способствующую развитию личинок вредных насекомых, например, комаров.

При проектировании канализационных труб устанавливают величину минимальной незаиляющей скорости для труб d < 500 мм. V_min= 0,7 м/с, а для труб

d > 500 мм V_min=0,8 м/с. Максимально допустимая скорость для канализационных труб и каналов, выполненных из кирпича, бетона, керамики и других неметаллических материалов может быть принята равной не более 5 м/с. Для металлических труб – не более 10 м/с. При этом в сточных водах учитывается наличие твердых частиц.

1.8 Расчет каналов, имеющих составной поперечный профиль.

Этот профиль (рис 1.5) нельзя рассчитывать, следуя вышеизложенному методу. Здесь следует поступать следующим образом:

B B B B

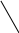
1 2 3

A А

Рис 1.5

Здесь следует поступать следующим образом: проводим линии AB или линии A B . При этом разбиваем сечение на отдельные части 1,2,3. Далее каждую выделенную часть рассчитываем как самостоятельный канал определяя для каждой части свой расход и затем суммируя их.

1.9 Расчет каналов, имеющих замкнутый поперечный профиль

Каналами с замкнутым поперечным профилем являются канализационные и дренажные трубы, гидротехнические тунели. Эти водотоки работают как безнапорные.

а) Канализационные трубы

Канализационные трубы могут иметь следующие сечения:

а) круговое сечение – наиболее распространенный тип

б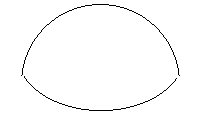 ) овоидальное (яйцевидное) – применяется при значительных колебаниях величины расхода стоков.

в ) лотковое сечение – применяется для устройства ливневой канализации.

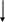
а) б) в)

Рис 1.6

h – глубина наполнения; d – полная высота профиля; h/d = a – степень наполнения. а принимают равной 0,5 – 0,8 . При этом меньшее относительное наполнение соответствует трубам меньшего диаметра (d <150 мм), большее – трубам, диаметр которых d > 900 мм.

Представим замкнутый профиль любого очертания. Предположим, что при

i = const глубина наполнения этого профиля изменяется от h = 0 до h = d. При этом средняя скорость V и расход Q будут изменяться от нуля до некоторых величин V_п и Q_п , отвечающих полному наполнению канала. Существенным является то обстоятельство, что функции V =(h) и Q = (h) в случае замкнутых профилей имеют максимум ,чего не наблюдается для открытых русел. Это обстоятельство объясняется резким увеличением смоченного периметра при наполнениях близких к полному при одновременном весьма малом увеличении живого сечения. Непосредсвенным расчетом по формуле Шези может быть показано: глубина, отвечающая V_max = (0,80 – 0,85)d, а глубина, отвечающая Q_max=(0,93 –0,95) d.