1) То у стаціонарній точці функція має екстремум: — точка максимуму; — точка мінімуму;

2) — у точці функція не має екстремуму;

3) — сумнівний випадок.

1.3.4. Гессіан

Другий диференціал функції багатьох змінних

(13)

є симетричною квадратичною формою відносно диференціалів незалежних змінних .

_{Означення. Матриця квадратичної форми (13), елемен- ти якої є частинними похідними другого порядку функції}

_тобто

_{називається матрицею Гессе:}

_{. (14)}

Визначник матриці Н називається гессіаном.

У частинному випадку функції двох змінних достатні умови екстремуму з використанням гессіана формулюються так.

Теорема 1.22. Нехай функція z = f(x, y) двічі неперервно диференційовна в околі стаціонарної точки (x₀, y₀). Тоді точка (x₀, y₀):

1) Є точкою мінімуму, якщо в ній

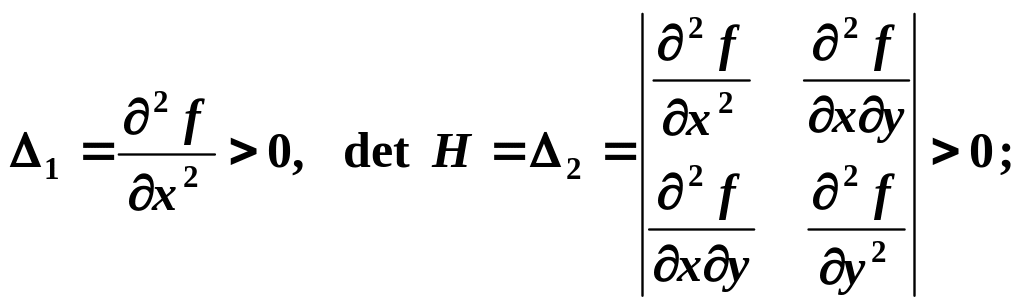
2) Є точкою максимуму, якщо в ній

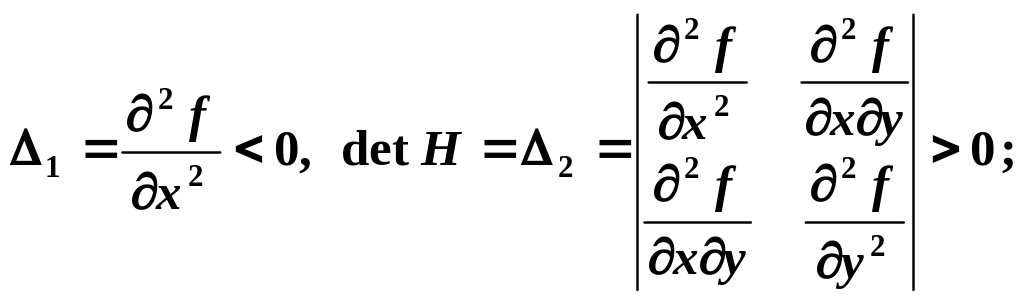
3) Не є точкою екстремуму, якщо

4) потрібне додаткове дослідження за допомогою диференціалів вищих порядків, якщо

.

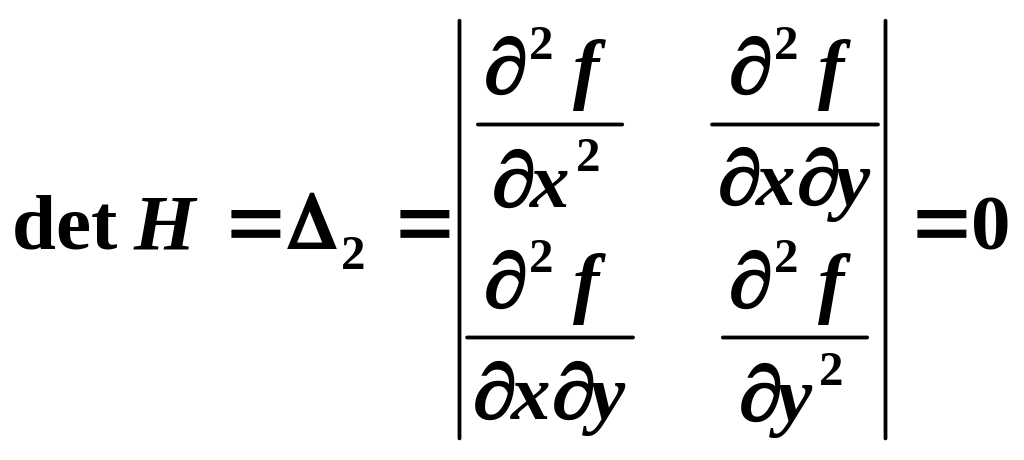Д ослідити функцію на екстремум.

^● 1. Знаходимо частинні похідні першого порядку:

,

2. Розв’язавши систему рівнянь

знаходимо стаціонарні точки і

3. Обчислюємо частинні похідні другого порядку:

,

4. У точці визначники ∆₁ і ∆₂ відповідно такі:

∆₁ = 6 > 0,

У точці маємо:

∆₁ = – 6,

5. Отже, за теоремою 1.22 точка є точкою мінімуму; у точці екстремуму немає.

Обчислюємо значення функції в точці мінімуму:

.

Д ослідити функцію на екстремум.

1. Знайдемо частинні похідні першого порядку:

.

2. Розв’язавши систему

знайдемо стаціонарну точку .

3. Обчислимо частинні похідні другого порядку:

4. Матриця Гессе має вигляд:

.

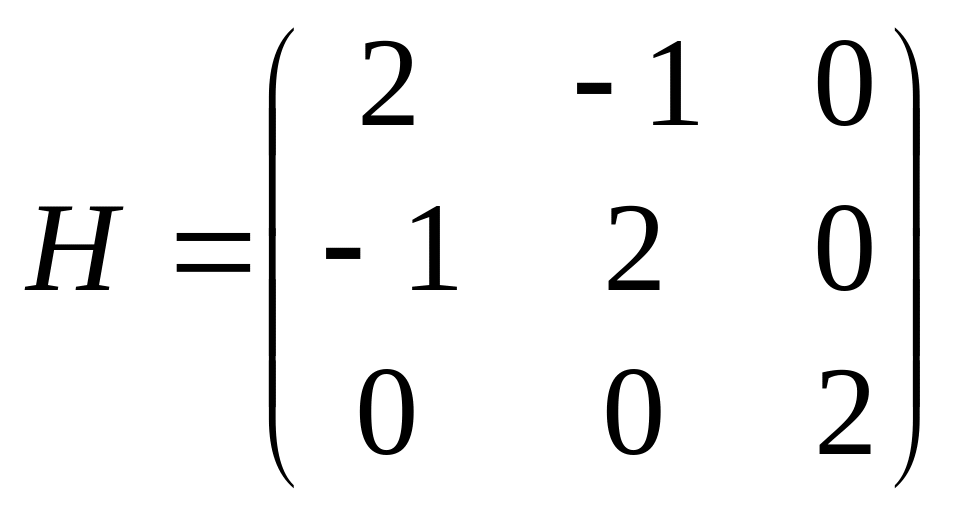5. У точці всі головні мінори цієї матриці додатні: ₁ = 2, ₂ = 3, ₃ = 6.

Отже, у точці функція має мінімум

.

1.3.5. Поняття умовного екстремуму

Нехай на відкритій множині задано функції

і нехай Е — множина точок, координати яких задовольняють рівняння

(15)

Рівняння (15) називаються рівняннями зв’язку, або обмеженнями.

Означення. Точка називається точкою умов­ного максимуму функції відносно рівняння зв’язку (15), якщо існує такий окіл точки х⁰, для всіх точок якого, що задовольняють рівняння зв’язку, виконується нерівність:

Якщо за цих умов виконується нерівність

то точку називають точкою умовного мінімуму функції при обмеженнях (15).

Ф ункція z = xy відносно рівняння зв’язку у точці (0, 0) має умовний мінімум, бо z = (0, 0) = 0, а в точках (, ), що задовольняють рівняння зв’язку, значення функції додатні.

Означення. Точки умовного максимуму і мінімуму називають точками умовного екстремуму. Умовний екстремум називають іноді відносним екстремумом.

Геометрична інтерпретація (рис. 1.28).

Рис. 1.28

1.3.6. Прямий метод знаходження точок умовного екстремуму (Метод виключення)

Якщо рівняння зв’язку

, , (16)

можна розв’язати відносно m змінних, наприклад, відносно змінних :

……………………

,

то дослідження функції на умовний екстремум при обмеженнях (16) зводиться до дослідження на звичайний (безумовний) екстремум функції змінних :

.

З найти умовний екстремум функції відносно рівнянь зв’язку:

,

^● Розв’яжемо рівняння зв’язку відносно змінних x i y:

,

Підставимо знайдені значення x i y у вираз для u та зведемо задачу до дослідження на безумовний екстремум функції

, , якщо ;

тому — точка максимуму функції.

Отже, задана функція у точці має умовний максимум, що дорівнює

1.3.7. Метод Лагранжа знаходження точок умовного екстремуму

Нехай функції , , , неперервно диференційовні в околі точки і ранг матриці Якобі

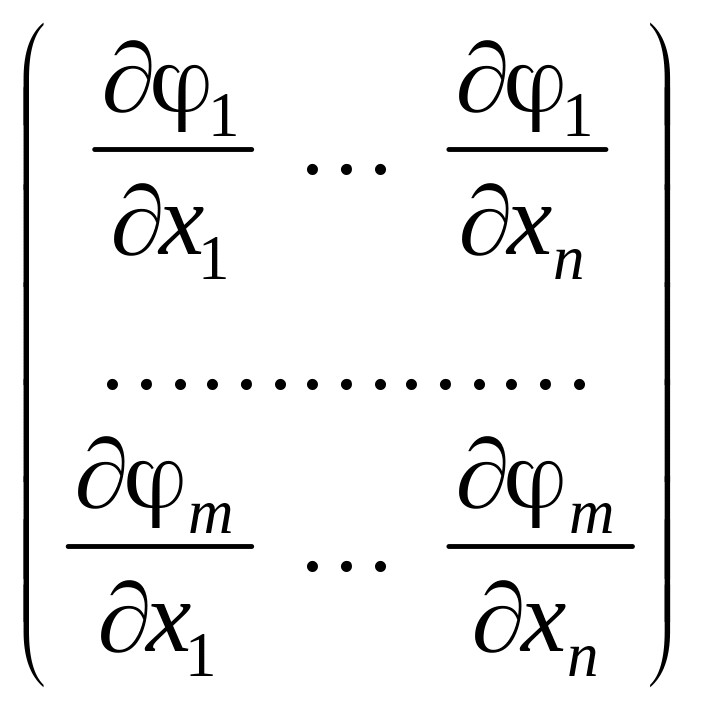(17)

у цій точці дорівнює m.

Означення. Функцію називають функцією Лагранжа, параметри — множниками Лагранжа.

Теорема 1.23. (Необхідна умова існування умовного екстремуму). Для того щоб точка була точкою умовного екстремуму функції при рівняннях зв’язку , необхідно, щоб її координати при деяких значеннях задовольняли систему рівнянь:

Умови (18), (19) означають, що точка є стаціонарною точкою функції Лагранжа і її координати задовольняють рівняння зв’язку.

Доведення. Запишемо рівності виду (18)

, (20)

де, як і раніше, означають диференціали неявних функцій; похідні обчислені в точці

Візьмемо значення множників так, щоб перетворювалися на нуль коефіцієнти при залежних диференціалах :

(21)

.

Це зробити можна, оскільки визначник системи лінійних рівнянь (20), з яких визначаються , відмінний від нуля. При вибраних значеннях множників (20) набере вигляду

(22)

Тут ми знову маємо лише диференціали незалежних змінних, тому коефіцієнти при них мають бути нулями. Отже, поряд з (21) дістаємо

. (23)

Тепер для визначення невідомих та ще m множників маємо стільки ж рівнянь — m рівностей зв’язку і рівнянь:

.

Для того щоб спростити запис цих рівнянь, звичайно вводять допоміжну функцію

.

Тоді зазначені рівності можна подати у вигляді

. (24)

Теорема 1.24. (Достатня умова умовного екстремуму.) Нехай функції , , , двічі неперервно диференційовні в околі точки і нехай у цій точці виконуються необхідні умови існування екстремуму функції при обмеженнях (19).

Тоді в разі виконання умов

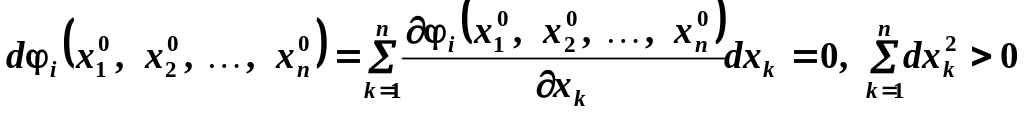(25)

другий диференціал функції Лагранжа є додатно (від’ємно) визначеною квадратичною формою. А це означає, що функція у точці має умовний строгий мінімум (максимум).

Якщо за умов (25) другий диференціал є невизначеною квадратичною формою, то в точці умовного екстремуму немає.

Доведення. Припустимо існування і неперервність інших по- хідних для функцій f і . Нехай тепер точка разом із множниками задовольняє сфор­мульовані раніше необхідні умови.

Висновок про існування в цій точці (відносного) екстремуму залежить від знака різниці

,

з тим лише істотним застереженням, що і точка задовольняє рівняння зв’язку (19). Легко зрозуміти, що для таких точок приріст функції f можна замінити на приріст функції L (де всі множники ми вважаємо такими, що дорівнюють ):

.

Оскільки в точці виконуються умови (24) — у цьому й полягає сенс переходу до функції L, — зазначений приріст можна записати за формулою Тейлора:

,

де

,

і , якщо (останні прирости при цьому самі собою будуть нескінченно малими згідно з неперервністю функцій (21)).

Якщо замінити тут усі прирости відповідними диференціалами , то стосовно незалежних змінних нічого не зміниться. Що ж до залежних змінних, то така заміна зумовлює лише необхідність узяти замість коефіцієнтів інші нескінченно малі :

.

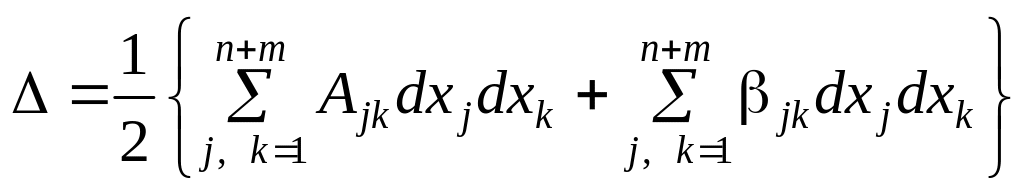Перехід до диференціалів зручний, оскільки диференціали залежних і незалежних змінних пов’язані системою лінійних співвідношень. З огляду на те, що визначник системи (20) у точці , за припущенням, — не нуль, то залежні диференціали можна лінійно подати через незалежні. Підставивши їх вирази у , замість першої суми дістанемо квадратичну форму відносно диференціалів .

А тепер можна показати, що коли ця форма буде визначеною і притому додатною (від’ємною), то в досліджуваній точці досягатиметься відносний мінімум (максимум), а якщо форма невизначена, то відносного екстремуму немає.

З найти умовний екстремум функції відносно рівняння зв’язку .

^● Функції u і  двічі неперервно диференційовні. Ранг матриці Якобі (17) в даному разі дорівнює 1 у всіх точках, що задовольняють рівняння зв’язку. Отже, можна скористатися методом Лагранжа. Запишемо функцію Лагранжа

.

Згідно з необхідними умовами (18), (19) дістанемо систему

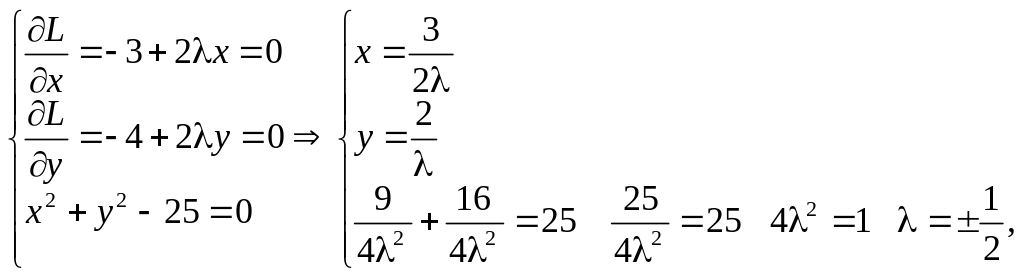
з якої знайдемо , при і , при . Отже, функція u може мати умовний екстремум лише у двох точках: і . Обчислимо другий диференціал функції Лагранжа:

; , ,

звідки .

Знайдемо перший диференціал функції : У точ­ках і диференціали і , пов’язані рівністю:

, або .

У разі виконання цієї умови другий диференціал функції Лагранжа в точці є додатно визначеною квадратичною формою

,

а в точці — від’ємно визначеною формою

.

Отже, функція u в точці має умовний мінімум, а в точці — умовний максимум.