
- •1.3. Дослідження функцій багатьох змінних
- •1.3.1. Поняття екстремуму функції багатьох змінних
- •1.3.2. Необхідні умови існування екстремуму
- •1.3.3. Достатні умови існування екстремуму
- •1) Є точкою мінімуму функції, якщо
- •2) Є точкою максимуму функції, якщо
- •3) Не є точкою екстремуму, якщо набуває як додатних, так і від’ємних значень.
- •Нагадаємо, що у вищій алгебрі квадратичну форму
- •1) То у стаціонарній точці функція має екстремум: — точка максимуму; — точка мінімуму;
- •1.3.4. Гессіан
- •1) Є точкою мінімуму, якщо в ній
- •2) Є точкою максимуму, якщо в ній
- •3) Не є точкою екстремуму, якщо
- •1.3.5. Поняття умовного екстремуму
- •1.3.6. Прямий метод знаходження точок умовного екстремуму (Метод виключення)
- •1.3.8. Метод найменших квадратів
- •1.3.9. Вирівнювання за допомогою кривих
- •1. Вирівнювання за допомогою параболи
- •1.3.10. Найбільше та найменше значення функції багатьох змінних
- •1.3.11. Дотична площина до поверхні
- •1.3.12. Нормаль до поверхні
- •Алгоритм знаходження рівнянь обвідної в параметричному вигляді
1.3. Дослідження функцій багатьох змінних
1.3.1. Поняття екстремуму функції багатьох змінних
Для зручності обмежимо розгляд ФБЗ на прикладі функцій двох змінних. Нехай
Маємо функцію
![]() де D
– область
визначення даної функції. Виберемо
де D
– область
визначення даної функції. Виберемо
![]() - деяку внутрішню
точку області D.
- деяку внутрішню
точку області D.
ОЗНАЧЕННЯ. Точка
![]() називається точкою
максимуму функції
називається точкою
максимуму функції
![]() ,
якщо існує окіл точки
такий що для всіх точок цього околу
виконується нерівність
,
якщо існує окіл точки
такий що для всіх точок цього околу
виконується нерівність
![]() .
.
(Для
більшої кількості змінних означення
формулюється аналогічно тільки
з’являються нові змінні![]() ).
).
ОЗНАЧЕННЯ. Точка називається точкою мінімуму функції , якщо існує окіл точки , для всіх точок якого виконується нерівність
![]() .
.
Точки максимуму і мінімуму називаються точками екстремуму.
Графічна інтерпретація точок екстремуму

Точка А — точка максимуму. Точка В — точка мінімуму
Рис. 1.3.1 Рис. 1.3.2
Можливий ще й такий варіант екстремальної точки: так звана сідлова точка (рис. 1.3.3).

Точка С — сідлова точка
Рис. 1.3.3
1.3.2. Необхідні умови існування екстремуму
Сформулюємо спочатку необхідні умови існування точок екстремуму для функцій двох змінних.
Теорема 1.19*. (про
необхідні умови існування екстремум
уму функції двох змінних ) Якщо точка
![]() є точкою екстремуму функції
є точкою екстремуму функції
![]() ,
то її частинні похідні в цій
точці дорівнюють нулю, або не існують.
,
то її частинні похідні в цій
точці дорівнюють нулю, або не існують.
Доведення. Введемо в розгляд
функцію однієї змінної припустивши, що
змінна
![]() є сталою і дорівнює
є сталою і дорівнює
![]() ,
тобто маємо ФОЗ
,
тобто маємо ФОЗ
![]() ,
яка визначена за умовою в деякому околі
точки
,
яка визначена за умовою в деякому околі
точки
![]() дійсної осі. Таким чином для отриманої
функції однієї змінної справедлива
теорема про необхідні умови існування
екстремуму, тобто оскільки точка
за умовою є
точкою екстремуму, то і відповідна її
координата
також точка екстремуму функції
дійсної осі. Таким чином для отриманої
функції однієї змінної справедлива
теорема про необхідні умови існування
екстремуму, тобто оскільки точка
за умовою є
точкою екстремуму, то і відповідна її
координата
також точка екстремуму функції
![]() .
Тоді, оскільки
.
Тоді, оскільки
![]() ,
,
або ж якщо не існує
![]() ,
то не існуватиме й
,
то не існуватиме й
![]() .
Аналогічно припустивши, що змінна
.
Аналогічно припустивши, що змінна
![]() є сталою і дорівнює
,
отримаємо ФОЗ
є сталою і дорівнює
,
отримаємо ФОЗ
![]() для якої справедливо
для якої справедливо
![]()
або ж якщо не існує
![]() ,
то не існуватиме й
,
то не існуватиме й
![]() .
Теорему доведено.
.
Теорему доведено.
На практиці перевірка необхідних умов існування екстремуму зводяться до перевірки істинності системи
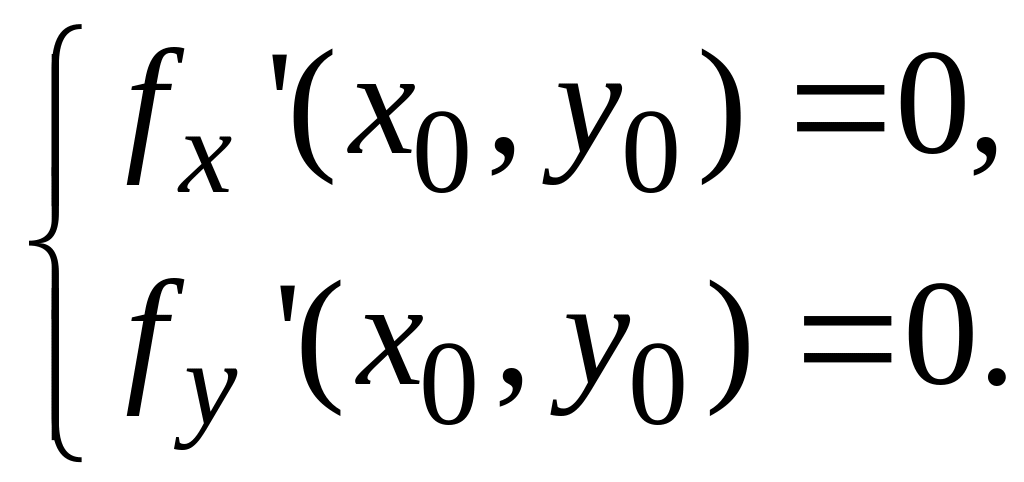
Для випадку функції
![]() -
змінних справедлива наступна теорема.
-
змінних справедлива наступна теорема.
Теорема 1.20. Для
точки екстремуму
![]() функції
функції
![]() частинні похідні
частинні похідні
![]() або дорівнюють нулю, або не існують.
або дорівнюють нулю, або не існують.
Доведення. Розглянемо функцію
![]() однієї змінної, визначеної умовами
теореми в деякому околі точки
однієї змінної, визначеної умовами
теореми в деякому околі точки
![]() дійсної осі. У точці
дійсної осі. У точці
![]() функція
функція
![]() має екстремум. Тоді, оскільки
-
точка екстремуму ФОЗ справедливо
має екстремум. Тоді, оскільки
-
точка екстремуму ФОЗ справедливо
 ,
,
або ж
![]() не існує, тоді і
не існує, тоді і
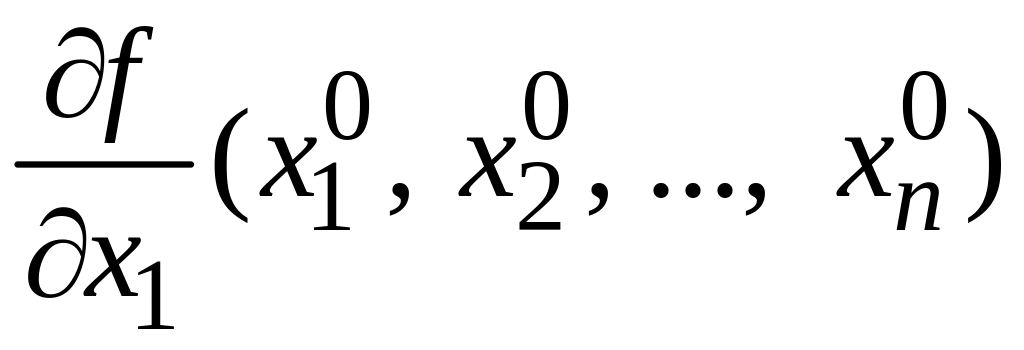 теж не існує (за теоремою для функції
однієї змінної). Аналогічно доводимо
випадки
теж не існує (за теоремою для функції
однієї змінної). Аналогічно доводимо
випадки
![]() .
Що й треба було довести.
.
Що й треба було довести.
На практиці перевірка необхідних умов існування екстремуму зводяться до перевірки істинності системи
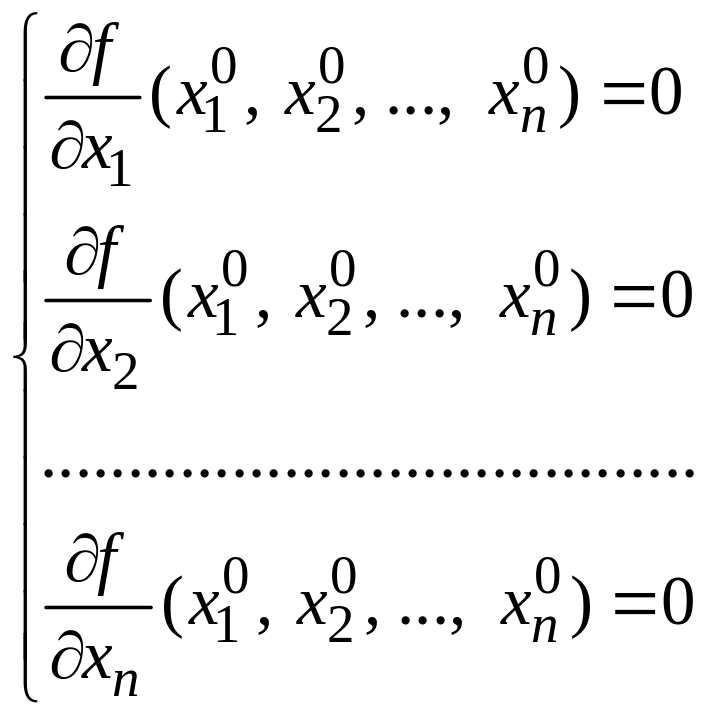
ОЗНАЧЕННЯ. Точки, в яких функція визначена, а її частинні похідні дорівнюють нулю або не існують, називають критичними (стаціонарними) точками цієї функції. На практиці їх знаходять розв’язуючи систему

відносно змінних
![]() .
.
Д![]() ля
функції
ля
функції
![]() усі точки осі х є критичними, бо в
кожній такій точці функція визначена,
усі точки осі х є критичними, бо в
кожній такій точці функція визначена,
![]() ,
а
,
а
![]() не існує. Точки екстремуму функції слід
шукати лише серед її критичних точок.
не існує. Точки екстремуму функції слід
шукати лише серед її критичних точок.
Якщо для функції
![]() у точці екстремуму існують частинні
похідні за всіма змінними, то всі вони
дорівнюють у цій точці нулю:
у точці екстремуму існують частинні
похідні за всіма змінними, то всі вони
дорівнюють у цій точці нулю:
![]() (1)
(1)
Умови (1) не є достатніми умовами існування екстремуму.
Д
ля
функції
![]() умови (1) виконуються в початку координат,
але ця точка не є екстремальною для
розглядуваної функції.
умови (1) виконуються в початку координат,
але ця точка не є екстремальною для
розглядуваної функції.
ЗАУВАЖЕННЯ!!! Точки екстремуму диференційовної функції слід шукати лише серед її стаціонарних точок.
