Диференційовність функції двох змінних

11. Частинні та повні прирости функції двох змінних

Нехай функція визначена в деякому околі точки . Тоді надамо незалежним змінним х та у приростів х і у так, щоб точка не виходила за межі зазначеного околу і точки , також потраплять у цей окіл (рис. 1.19).

Рис. 1.19

ОЗНАЧЕННЯ. Повним приростом функції f по х та у при переході від точки до точки називають різницю

яку позначають .

Аналогічно позначимо частинним приростом по х функції називатимемо різницю

Частинним приростом по у цієї функції називаємо

Таким чином

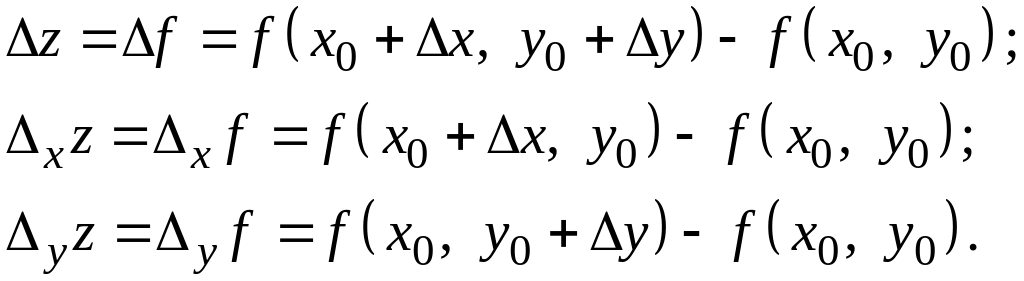
З ауваження. Аналогічно визначаються прирости функції більш ніж двох змінних, наприклад для

.

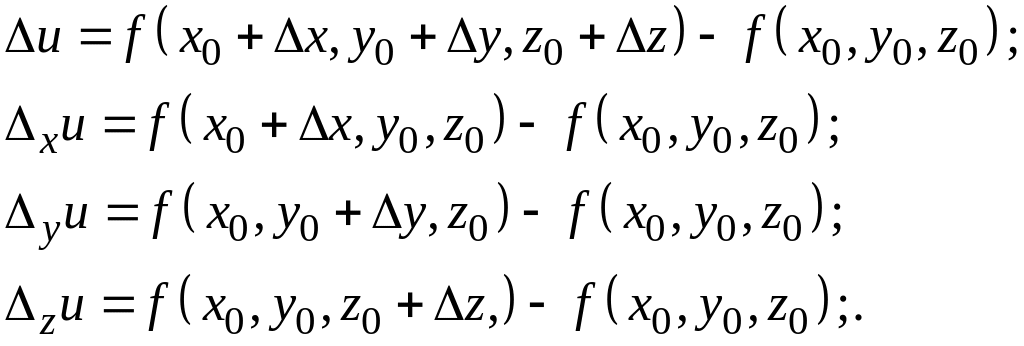
З найти прирости функції в точці , якщо

Використовуючи формули отримаємо

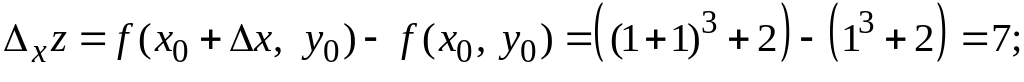
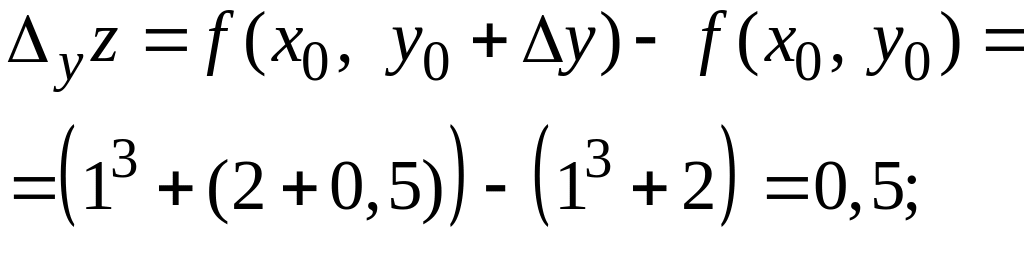
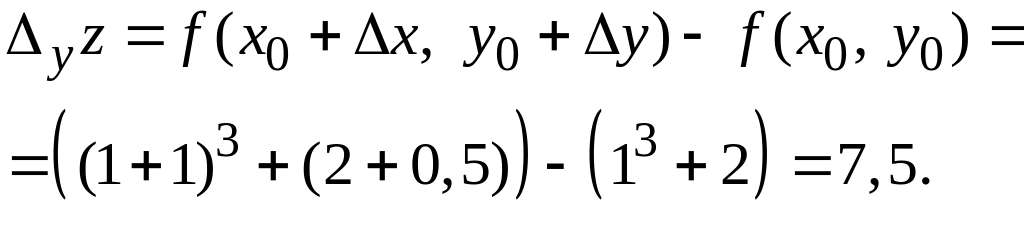
З найти прирости функцій

в точці , якщо

___________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________

12. Частинні похідні функції двох змінних

Нехай функція задана в деякому околі точки .

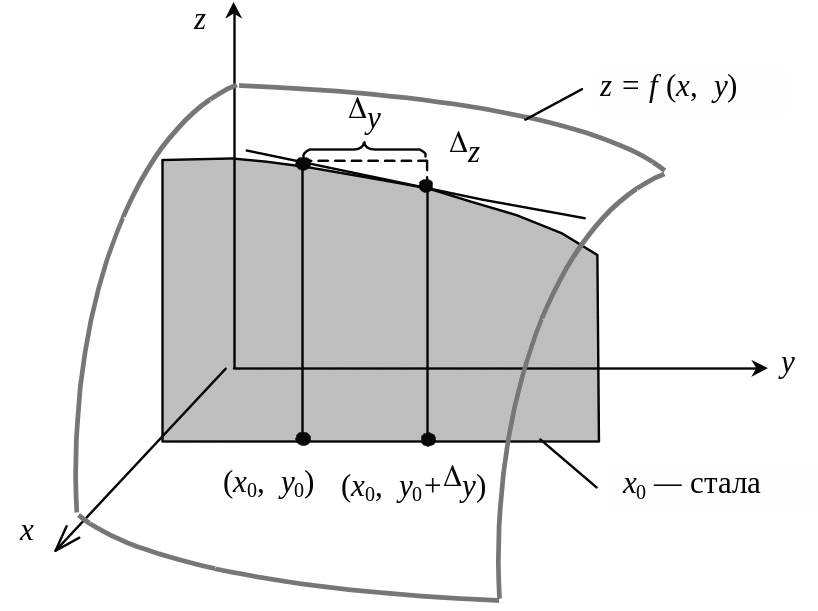
Рис. 1.20

ОЗНАЧЕННЯ. Частинними похідними функції z = f(x, y) у точці відповідно за змінними х і у називають скінченні границі

;

,

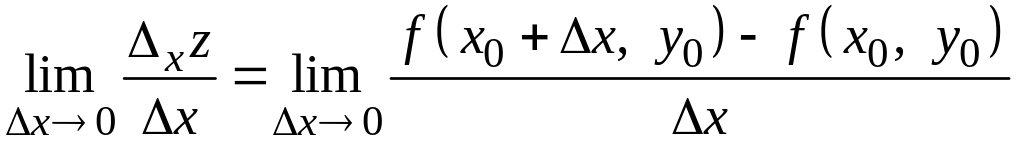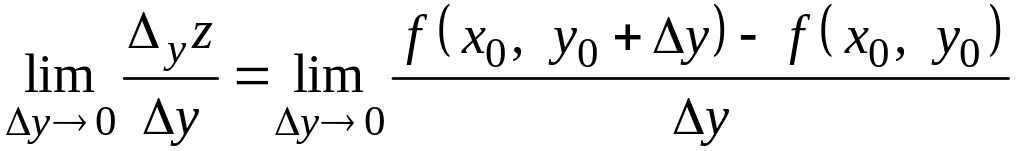звісно, якщо вони існують. Їх позначають: 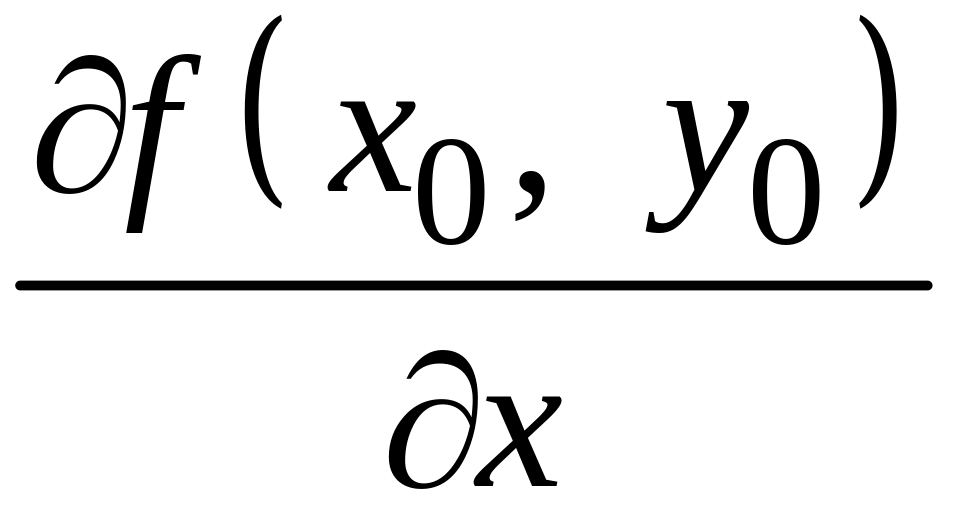, або , або (Символ «» — читають «де» вперше застосував відомий математик Якобі.)

На практиці зручно використовувати наступні формули

;

.

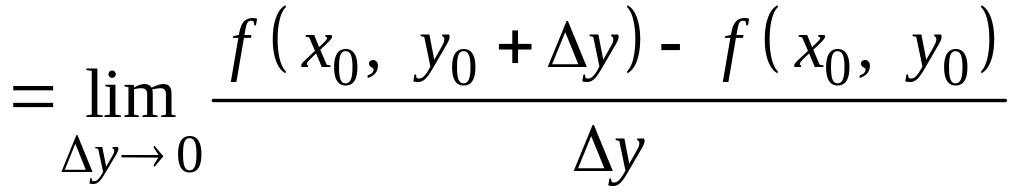Зауваження. Якщо в задачі не задають конкретну точку то у вищезазначених формулах потрібно замінити цю точку на довільну . Таким чином справедливі формули

;

.

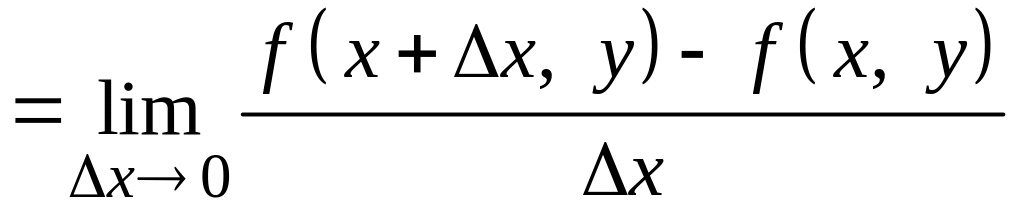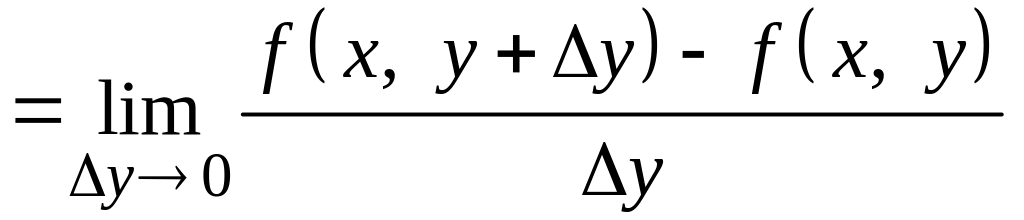О бчислити частинні похідні, використовуючи означення, від функції

Спочатку обчислимо частинні прирости

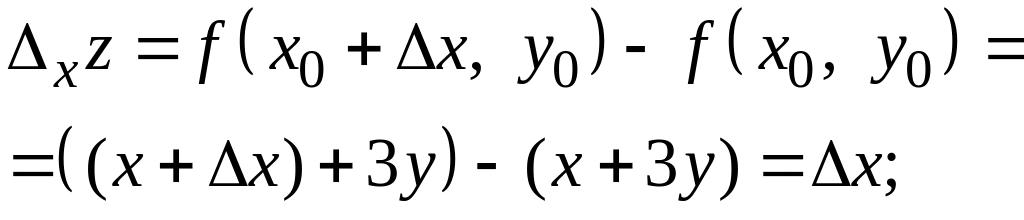
Тоді

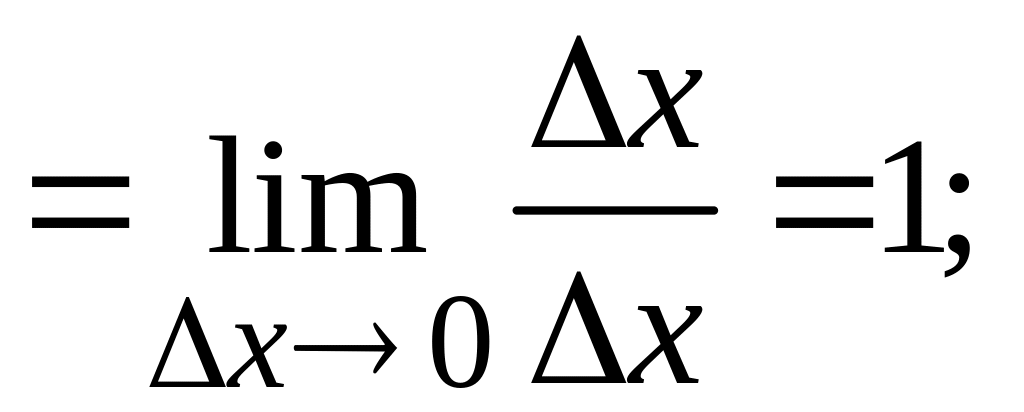
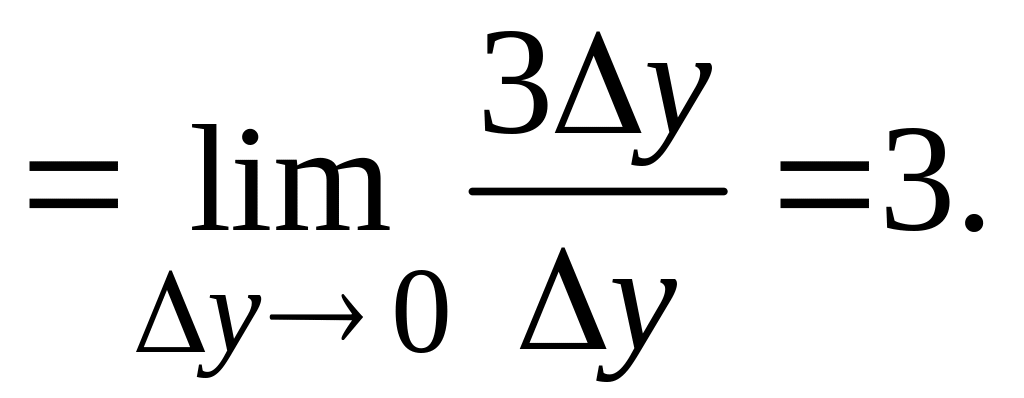
О бчислити частинні похідні, використовуючи означення, від функцій

_________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________

13. Повний диференціал функції двох змінних

ОЗНАЧЕННЯ. Функція називається диференційовною в точці , якщо її повний приріст можна подати у вигляді:

де А, В — деякі числа, які не залежать від приростів ; ,  — нескінченно малі при , ,тобто

.

Головна лінійна частина приросту функції, тобто

,

називається повним диференціалом функції (або першим диференціалом) у точці і позначається або Таким чином,

(1)

Диференціалом незалежної змінної x або y називають її приріст, тобто за означенням беруть

,

Зазначимо, що знак рівності є умовним, величини не однакові, вони відрізняються на нескі­нченно малу величину. Тому враховуючи більш точне співвідношення

отримаємо формулу наближеного обчислення значень функцій

або,що те саме

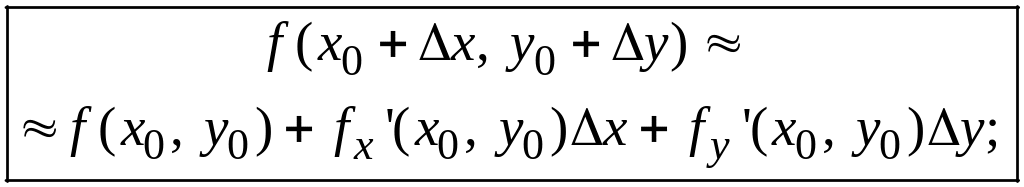
Н аближено обчислити не використовуючи калькулятор

Спочатку запишемо функцію, яка максимально відповідає даному виразу

.

Тепер виберемо точку з якої легко обчислюється корінь а значення змінних мало відрізняється від початкових. Нехай

Враховуючи, що

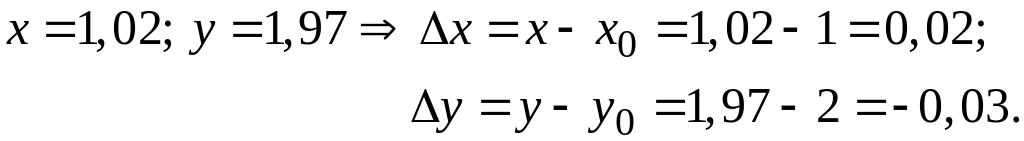
Знайдемо частинні похідні Враховуючи, що отримаємо

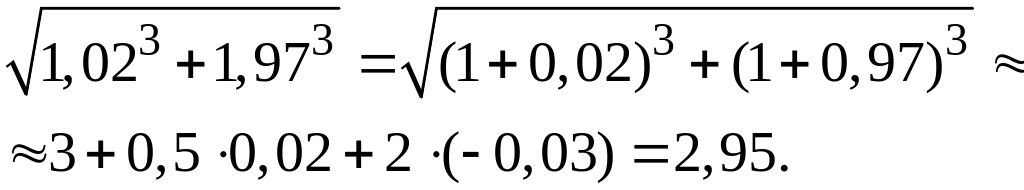
Н аближено обчислити не використовуючи калькулятор

________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________

Н аближено обчислити не використовуючи калькулятор

_________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________

ОЗНАЧЕННЯ. Якщо функція f диференційовна в кожній точці множини , то її називають диференці­йовною на множині D.

Отже, у кожній точці, де виконується рівність (1), повний диференціал функції обчислюється за формулою

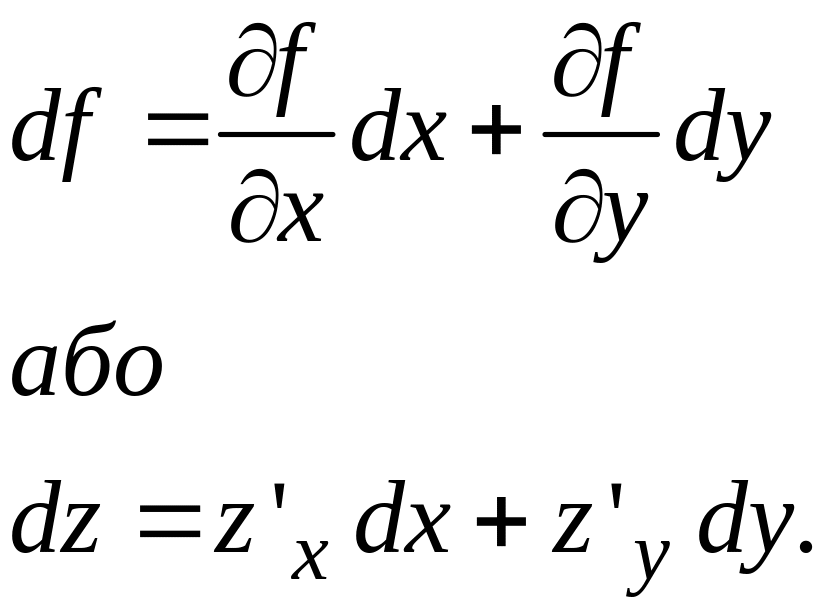(2)

Теорема 1.15. Якщо функція диференційовна в точці і , то в точці існують частинні похідні

,

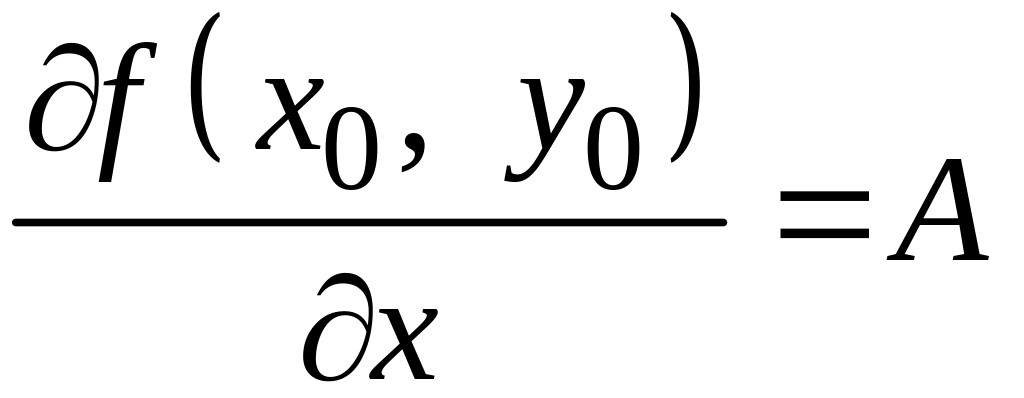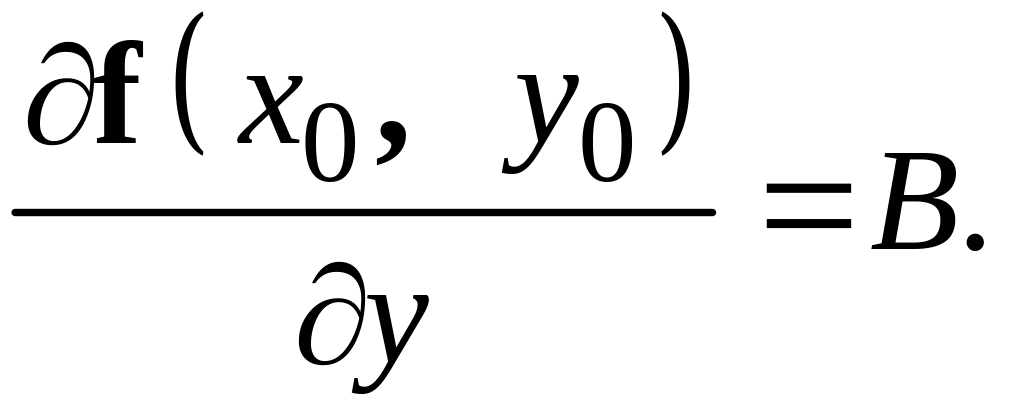
Доведення. За означенням диференційовної функції маємо:

(3)

Поклавши у (3) , дістанемо :

.

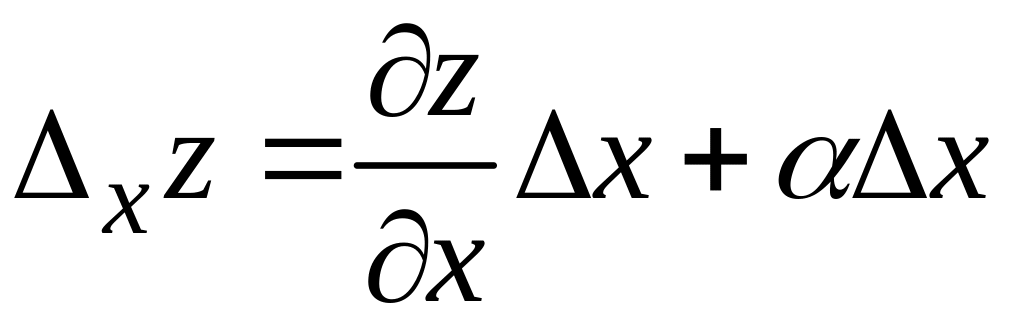
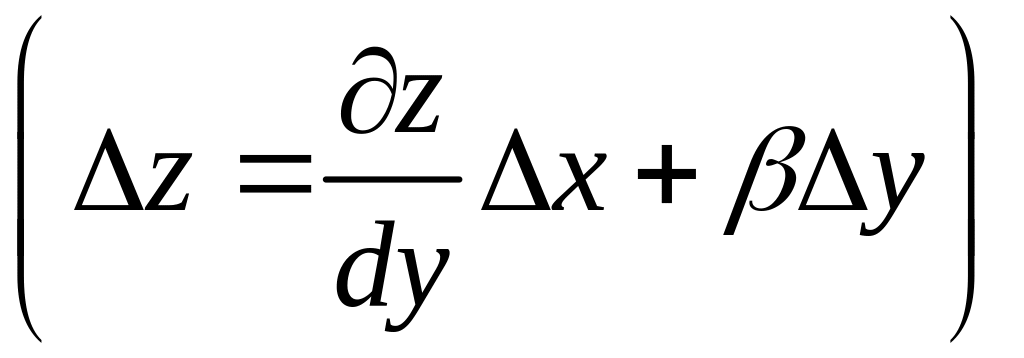Звідси

.

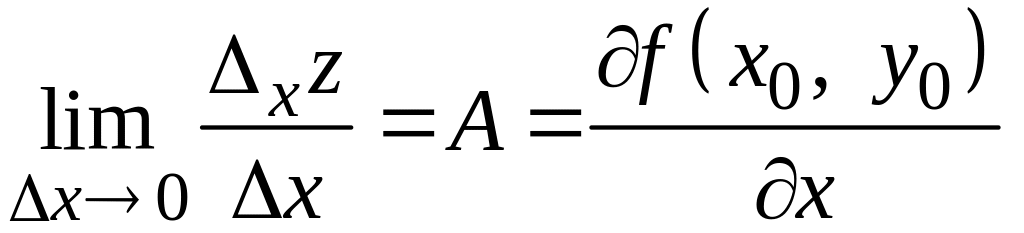
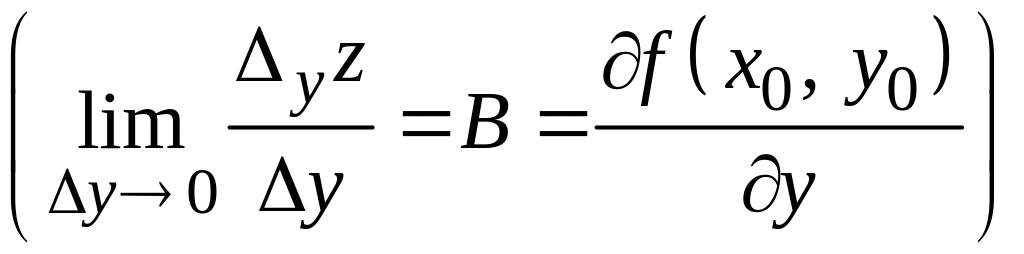Якщо частинні похідні функції f існують у кожній точці множини , то говорять, що функція f має частинні похідні на множині D.

Аналогічно визначають і позначають частинні похідні трьох і більше змінних.

14. Частинні похідні та повний диференціал функції n-змінних

Означення. Якщо існує скінченна границя

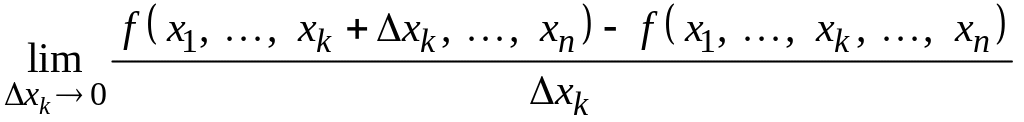
то її називають частинною похідною функції f у точці за змінною і позначають

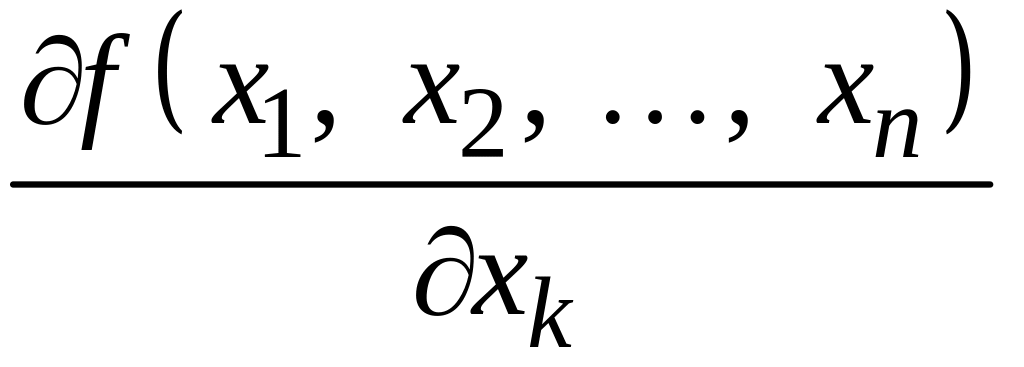або .

Похідні 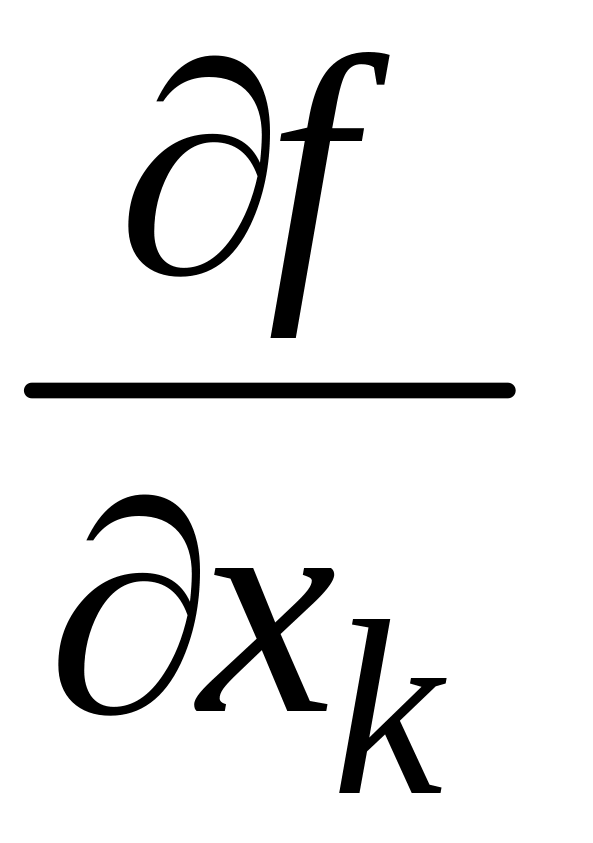, називають похідними першого порядку.