
Индивидуальные задания
Задание 1.
Для данного опыта
описать
пространство элементарных событий
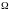 ,
подмножество, соответствующее случайному
событию
,
подмножество, соответствующее случайному
событию
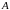 .
Привести пример события: а)
.
Привести пример события: а)
 ,
совместного с
б)
,
совместного с
б)
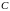 ,
несовместного с
,
в) достоверного, г) невозможного. Описать
события:
,
несовместного с
,
в) достоверного, г) невозможного. Описать
события:
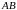 ,
,
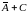 .
Найти
.
Найти
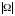 ,
,
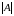 .
.
1.1. Монета
подбрасывается три раза,
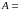 {герб
выпал не менее двух раз}.
{герб
выпал не менее двух раз}.
1.2. Из полного набора костей домино вынимается одна кость, {вынули дубль}.
1.3. Бросаются две игральные кости, {сумма выпавших очков делится на 4}.
1.4. Баскетболист три раза бросает мяч по кольцу, {первое попадание было на 3-ем броске}.
1.5. Стрелок три раза стреляет по мишени, {не менее двух попаданий}.
1.6. Из множества всех двузначных чисел выбирается одно число, {сумма цифр равна 7}.
1.7. Из всех карт красной масти наудачу выбирают две, {обе карты старше десятки}.
1.8. Монета подбрасывается три раза, {герб выпала только один раз}.
1.9. Игральная кость бросается дважды, {оба раза выпало четное число очков}
1.10. Из множества двузначных чисел от 15 до 30 выбирается одно число, {число делится на 6}.
1.11. Монета подбрасывается три раза, {герб выпал не более двух раз}.
1.12. Из полного набора костей домино вынимается одна кость, {сумма очков меньше 8}.
1.13. Бросаются две игральные кости, {сумма выпавших очков больше 8}.
1.14. Баскетболист три раза бросает мяч по кольцу, {не более одного промаха}.
1.15. Стрелок три раза стреляет по мишени, {первое попадание было на 2-ом броске}.
1.16. Из множества всех двузначных чисел выбирается одно число, {сумма цифр меньше 5}.
1.17. Из всех карт черной масти наудачу выбирают одну, {карта старше девятки}.
1.18. Монета подбрасывается три раза, {на втором броске выпала решка}.
1.19. Игральная кость бросается дважды, {сумма выпавших очков больше 10}
1.20. Из множества двузначных чисел от 25 до 40 выбирается одно число, {число делится на 4}.
1.21. Монета подбрасывается три раза, {герб выпал два раза}.
1.22. Из полного набора костей домино вынимается одна кость, {сумма очков больше 6}.
1.23. Игральная кость бросается дважды, {сумма выпавших очков меньше 8}.
1.24. Из множества двузначных чисел от 15 до 45 выбирается одно число, {число делится на 8}.
1.25. Из всех карт черной масти наудачу выбирают две, {обе карты младше 8}.
1.26. Игральная кость бросается дважды, {сумма выпавших очков делится на 3}.
1.27. Из колоды из 36 карт вынимают 5 карт, {среди пяти карт хотя бы одна дама}.
1.28. Игральная кость бросается дважды, {сумма выпавших очков не делится на 4}.
1.29. Бросаются две игральные кости, {на костях выпадет одно и тоже число очков}.
1.30. Из колоды из 36 карт вынимают 5 карт, {среди двух карт 2 десятка и 1 дама}.
Задание 2.
2.1. В ящике имеется
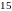 деталей, среди которых
деталей, среди которых
 окрашены. Сборщик наудачу извлекает
окрашены. Сборщик наудачу извлекает
 детали. Найти вероятность того, что
извлеченные детали окажутся окрашенными.
детали. Найти вероятность того, что
извлеченные детали окажутся окрашенными.
2.2. В ящике имеется
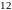 белых и
белых и
 красных шаров. Вынули
красных шаров. Вынули
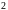 шара. Найти вероятность того, что они
разного цвета.
шара. Найти вероятность того, что они
разного цвета.
2.3. В ящике находится
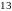 зеленых,
зеленых,
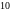 красных и
красных и
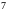 синих одинаковых шаров. Вынули
шаров. Найти вероятность того, что вынули
зеленых,
красных и
синих шара.
синих одинаковых шаров. Вынули
шаров. Найти вероятность того, что вынули
зеленых,
красных и
синих шара.
2.4. В ящике находится
 деталей, из них
бракованных. Наудачу извлечены
деталей, из них
бракованных. Наудачу извлечены
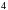 детали. Найти вероятность того, что
среди них нет бракованных.
детали. Найти вероятность того, что
среди них нет бракованных.
2.5. Устройство
состоит из
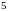 элементов, из которых две изношены. При
включении его включаются случайным
образом
элемента. Найти вероятность того, что
включенными окажутся неизношенные
элементы.
элементов, из которых две изношены. При
включении его включаются случайным
образом
элемента. Найти вероятность того, что
включенными окажутся неизношенные
элементы.
2.6. Студент знает
ровно
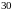 вопросов из
вопросов из
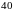 .
Найти вероятность того, что из
вопросов билета он знает ровно
.
.
Найти вероятность того, что из
вопросов билета он знает ровно
.
2.7. В ящике
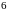 деталей первого сорта и
детали второго. Наудачу берут
детали. Найти вероятность того, что обе
– первого сорта.
деталей первого сорта и
детали второго. Наудачу берут
детали. Найти вероятность того, что обе
– первого сорта.
2.8. В коробке имеется одинаковых изделий, причем из них окрашены. Наудачу извлечены изделия. Найти вероятность того, что среди 2-х извлеченных изделий окажется: 1) только одно окрашенное изделие; 2) хотя бы одно окрашенное изделие; 3) два окрашенных изделия.
2.9. Рабочий
обслуживает
однотипных станка. Вероятность того,
что станок в течение часа потребует
наладки, равна
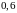 .
Предполагая, что станки работают
независимо, найти вероятность того, что
в течение часа потребуют наладки только
станка.
.
Предполагая, что станки работают
независимо, найти вероятность того, что
в течение часа потребуют наладки только
станка.
2.10. На складе находятся кинескопов, причем из них изготовлены Львовским заводом. Найти вероятность того, что среди наудачу взятых кинескопов окажутся кинескопа Львовского завода.
2.11. В ящике лежат белых и черных одинаковых на ощупь шаров. Вынули шаров. Какова вероятность того, что черных шаров вынуто не более трех?
2.12. В ящике лежат зеленых, красных, синих шаров, одинаковых на ощупь. Наудачу вынимают шаров. Какова вероятность того, что вынуты зеленых, красных и синих шара?
2.13. При бросании игральных костей вычислить вероятность того, что сумма выпавших очков больше их произведения.
2.14. В ящике, в
котором находится
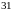 деталь без дефекта и
с дефектами, берут наудачу
детали. Чему равна вероятность того,
что, по крайней мере, одна деталь без
дефекта?
деталь без дефекта и
с дефектами, берут наудачу
детали. Чему равна вероятность того,
что, по крайней мере, одна деталь без
дефекта?
2.15. В партии из
деталей
нестандартные. Выбирается
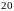 деталей. Найти вероятность того, что
среди них будет ровно
бракованных.
деталей. Найти вероятность того, что
среди них будет ровно
бракованных.
2.16. В урне белых и черных шара. Из урны вынимают случайным образом шара. Найти вероятность того, что среди них нет черных.
2.17. В ящике находится 5 белых и 3 красных шара. Наугад вынимают 3 шара. Найти вероятность того, что среди них два белых и один красный шар.
2.18. В коробке 30 конфет из них 10 с кофейной начинкой. Наугад берут 3 конфеты. Найти вероятность того, что среди них две конфеты с кофейной начинкой.
2.19. Бросается 10 одинаковых игральных костей. Найти вероятность того, что ровно на 3-х костях выпадет 6 очков.
2.20. Найти вероятность того, что в записи нечетного четырехзначного числа нет цифр 2 и 5.
2.21. Номер автомашины состоит из 4-х цифр. Найти вероятность того, что все цифры различны.
2.22. Найти вероятность того, что в записи четного четырехзначного числа нет цифр 1 и 9.
2.23. Цифры 1, 7, 5, 2 расположили в произвольном порядке. Найти вероятность того, что полученное число делится на 6.
2.24. Из цифр 1, 2, 3, …, 9 выбирают без возвращения и записывают в порядке выбора 4 цифры, образующие четырехзначное число. Найти вероятность того, что в записи числа нет цифры 2.
2.25. Из цифр 1, 2, 3, …, 9 выбирают без возвращения и записывают в порядке выбора 4 цифры, образующие четырехзначное число. Найти вероятность того, что сумма первой и последней цифры равна 10.
2.26. На полке 20 дисков, из них на 5-ти классическая музыка, на 8-ми рок-музыка, на 7-ми джаз. Наугад выбирают 5 дисков. Найти вероятность того, что среди них 3 диска с рок-музыкой и 2 с классической.
2.27. Цифры 4, 5, 7, 8, располагают в произвольном порядке. Найти вероятность того, что полученное число делится на 15.
2.28. Числа 1, 2, …, 9 записываются в случайном порядке. Найти вероятность того, что числа 3, 6, 9, будут следовать друг за другом в произвольном порядке.
2.29. Цифры 1, 2, …, 8 записываются в случайном порядке. Найти вероятность того, что числа 2, 3, 6, будут следовать друг за другом в произвольном порядке.
2.30. На карточках написано 10 различных вариантов контрольной работы. Они случайным образом распределяются среди восьми студентов, сидящих в одном ряду. Найти вероятность того, что варианты 1 и 2 достанутся рядом сидящим студентам.
