12.5. Змінний струм

Коли у контурі встановляться вимушені коливання, то їх можна розглядати як протікання змінного струму у колі, що містить у собі активний омічний опір R, індуктивність L та ємність C, викликаного прикладеною змінною напругою джерела струму

. (1)

Струм у колі задається виразом

I=I_ocos(t-), (2)

що відстає за фазою від на . Амплітуда струму визначається виразом

, , (3)

де величина Z називається повним електричним опором або імпедансом.

Якщо коло містить лише активний опір, то напруга на опорі

(4)

співпадає за фазою із струмом.

Якщо в колі міститься лише ємність С, то

. (5)

При цьому і струм випереджає за фазою напругу . Заміна конденсатора замкненою дільницею кола, як це видно з виразу для Z, означає перехід не до С=0, а до . Справді, замикання обкладок конденсатора означає, що відстань між ними d0, а .

Якщо в колі міститься лише індуктивність, то

. (6)

При цьому і струм відстає за фазою від напруги . Якщо в колі містяться ємність С та індуктивність L, то

. (7)

Величина Х називається реактивним опором або реактансом. Відповідно можна записати фазу та імпеданс Z через Х

. (8)

У загальному випадку потужність, що виділяється в колі змінного струму можна записати у вигляді

. (9)

Таким чином, миттєва потужність із подвоєною частотою коливається коло свого середнього значення , бо середнє значення .

Практичний інтерес представляє середнє значення потужності за період. Тепер середня потужність становить

. (12)

З фазової діаграми (див.Мал.1325) видно, що

.

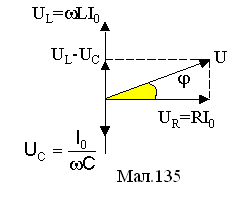Підставивши останній вираз для косинуса у вираз для середньої потужності і, врахувавши, що , одержимо

. (10)

Таку ж потужність розвиває сталий струм, сила якого дорівнює

I_o. (11)

Величина називається діючим або ефективним значенням сили змінного струму І_о, а величина

. (12)

називається діючим або ефективним значенням напруги. В термінах ефективних величин середню потужність можна записати у вигляді

. (13)

Множник cos називають коефіцієнтом потужності і чим він більше тим більша потужність виділяється в колі змінного струму. Максимальна потужність у колі виникне тоді, коли фаза =0.

12.6. Рівняння Максвелла

Повна система інтегральних або диференціальних рівнянь, що описують рух електромагнітного поля у просторі та часі називається рівняннями Максвелла. Для одержання повної системи рівнянь в інтегральному та диференціальному виді, потрібно попередньо розглянути теореми Остроградського-Гауса та Стокса й гіпотезу Максвелла щодо струму зміщення.

12.6.1.Теорема Остроградського-Гауса

Потік вектора , що визначає деяке силове поле, через довільну замкнену поверхню у цьому полі, дорівнює інтегралові від дивергенції вектора , взятому по об’єму , обмеженого поверхнею

, (1)

де

, (2)

, вектор нормалі до елементу dS, проекції вектора на осі x, y, z.

12.6.2.Теорема Стокса.

Циркуляція вектора , що визначає деяке силове поле, через довільний замкнутий контур у цьому полі, дорівнює потокові вектора rot (ротор ) через поверхню , натягнуту на контур

. (3)

Значення компонент вектора rot у декартових координатах дає визначник, розкритий через перший рядок (направляючі орти осей х, y, z)

(4)

і в явному вигляді їх можна записати так

. (5)