Тест по эконометрике

1. Что изучает эконометрика?

1. Принятие решений;2. Математические модели реальных экономических явлений;

3. Построение математических моделей;4. Измерение в эконометрике.

2. Под математической моделью понимается:1. Подобие исследуемого явления;

2. Отражение реального объекта;3. Система математических уравнений, неравенств, формул и различных математических уравнений;4. Система математических уравнений, неравенств, формул, графиков и различных математических выражений, описывающих реальный объект, составляющие его характеристики и взаимосвязи между ними.

3. Математическое моделирование относится к:1. Пространственному моделированию;2. Знаковому моделированию;3. Идеальному неформализованному моделированию;4. Идеальному формализованному моделированию.

4. Что положено в основу использования моделей для анализа экономических процессов:1. Статистическая закономерность;2. Принцип, называемый законом больших чисел;3.Социально-экономические явления и процессы производства;4. Закономерность, которая скрыта в числовых данных, характеризующих экономический процесс.

5. Математические модели должны:1. Описываться системой показателей;2. Не допускать проверку статистическими критериями;3. Позволять реализацию на ЭВМ не по стандартным программам;4. Строиться на базе достаточно большого числа недостоверных данных;5. Не способствовать выявлению скрытых причинно- следственных связей.

6. Экономические модели классифицируется как:1. а) модели структуры; б) аналитические модели ; в) статистические; 2. а) модели взаимосвязи; б) макроэкономические модели; в) отраслевые; 3. а) народнохозяйственные; б) региональные; в) районные; 4. а) модели структуры; б) модели взаимосвязи; в) модели динамики.

7. Построение экономических моделей распадается на следующие этапы: 1. а) качественный анализ экономического процесса; б) формирование первичной гипотезы в) анализ структурных связей г) проверки гипотезы об адекватности модели; 2. а) отбор экономических показателей, выступающих в роли переменных величин; б) анализ структурных связей; в) выбор и формирование типа связи; г) прогнозирование экономических показателей; 3. а) изучение сути исследуемого экономического процесса; б) анализ структурных связей; в) внутримодельное решение; г) оценка адекватности модели; 4. а) проведение качественного анализа экономического процесса для выявления причинно-следственных связей и определения факторных признаков и результативного признака б) выбор структуры модели и ее аналитической связи в) математическая оценка неизвестных параметров, входящих в аналитическую запись модели, исследование значимости оценок параметров; г)проверка адекватности модели.

8. Вероятностью события называется числовая неотрицательная функция P(A), определенная по элементам σ–алгебры и удовлетворяющая трем аксиомам: 1.а) всякий мыслимый результат эксперимента равен нулю; б) P(Ω)=-1; в) P(A₁ - A₂)= P(A₁)+P(A₂); 2. а) число, заключенное в пределах то 0 до 1; б) P(Ω)=-1; в) P(A₁ * A₂)= P(A₁)+P(A₂); 3. а) P(A)≥1; б) P(Ω)=0; в) , если A₁, A₂, … несовместны; 4. а) 0≤P(A)≤1; б) P(Ω)=1 в) если A_1,A_2, ….- несовместные события, то 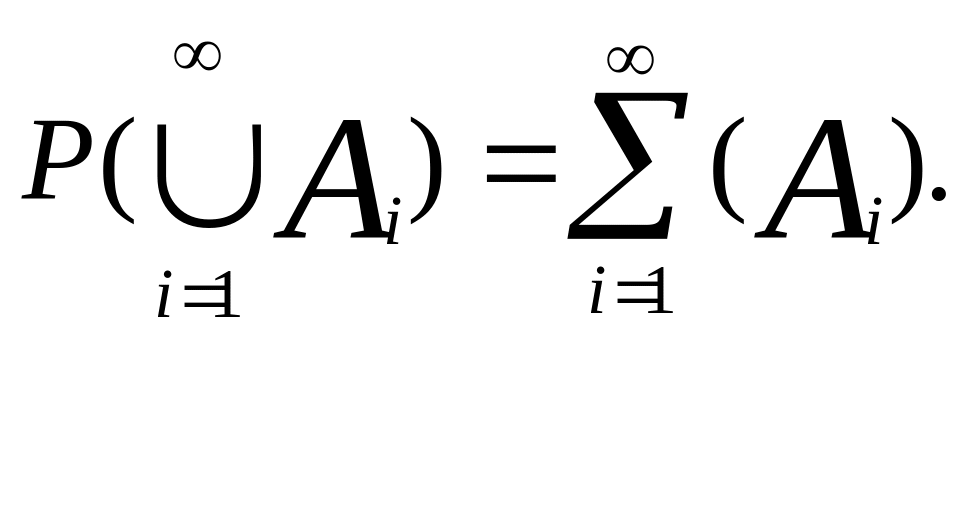9. Случайная величина - это величина, которая в результате реализации эксперимента принимает:1. значение равное 1; 2. любые значения; 3. конечное или счетное множество значений; 4. случайное значение неизвестное до реализации эксперимента.

10. Случайная величина называется дискретной, если: 1. ее значения равны 2. она принимает только значения равные нулю; 3. она принимает любые значения;

4. она принимает конечное или счетное множество значений.

11. Случайная величина называется непрерывной, если: 1. она принимает отдельные значения; 2. множество значений ее ограничено; 3. ее значения равны 4. множество ее значений сплошь заполняет некоторый промежуток числовой оси.

12. Математическим ожиданием дискретной и непрерывной случайных величин называются числа, вычисляемые по формулам:

1. a) 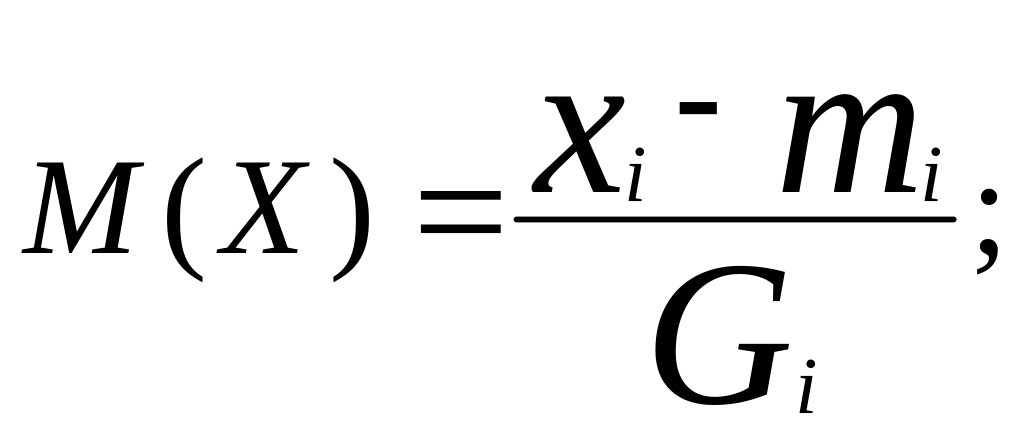б) M(X)=

2. а) M(X)= , б) M(X)=

3. а) M(X)= , б) M(X)=

4. a) M(X)= , б) M(X)=

Где x_i-значение ДСВ, p_i- их вероятности, р(х)- плотность распределения вероятностей НСВ.

13. Дисперсией дискретной и непрерывной случайных величин называются числа, вычисляемые по формулам:

1. а) б) D(X)=

2. а) б) D(X)=

3. а) б) D(X)=

4. а) б) D(X)=

где x_i – значения ДСВ; p_i – их вероятности; p(x) – плотность распределения НСВ; M(X) – математическое ожидание.

14. Закон распределения непрерывной случайной величины называется нормальным, если плотность распределения вероятностей р(х) имеет вид:

1.p(x)= ; 2. р(x)= ; 3. p(x)= ; 4. p(x)= ;

15. Случайная величина

имеет распределение xu-квадрата, если:

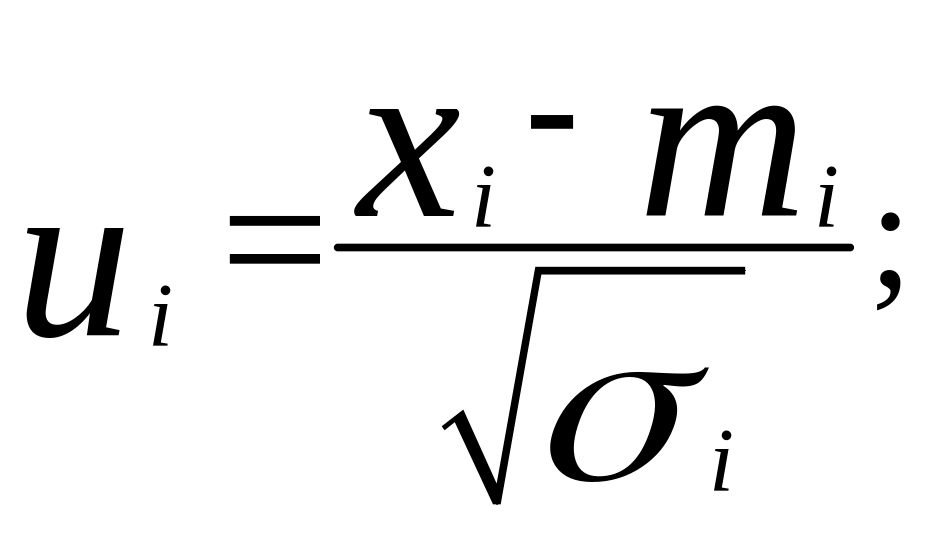1. , ; 2. ; 3. ; 4. .

16. Случайная величина Имеет распределение Стьюдента, если :

1.U V-распределение по закону χ² 2. U V

3. U V 4. U V-распределение по закону χ² с ν=n-1 степенями свободы

17. Случайная величина

Имеет распределение Фишера со степенями свободы ν₁=m и ν₂=n ,если:

1. U и V-независимые СВ;

2. U и V-независимые нормально распределенные СВ;

3. U- распределена по закону χ²; V-нормальное распределение;

4. U и V-независимые СВ, распределенные по закону χ² со степенями ν₁=m и ν₂=n ;

18. Закон распределения двумерной случайной величины (X;Y) задается в виде:

1. множества Ω_хy={ (x_1;y₁), (x_2;y₂ ),…,(x_i;y_j), …} 2.перечня вероятностей р (х _i, y_j);

3.множества слагаемых ; 4. таблица, в которой указаны значения случайных величин X и Y и соответствующие им вероятности.

19. Условным математическим ожиданием одной из случайных величин X и Y при

Y=y или X=x называется выражение:

1. ,

2. , ;

3. ;

4. ,

20. Что характеризует корреляционный момент и по какой формуле он вычисляется:

1. определяет характер случайных величин; вычисляется по формуле:

2. определяет зависимость случайных величин; вычисляется по формуле:

3. определяет не зависимость случайных величин; вычисляется по формуле

4.определяет взаимосвязь случайных величин; вычисляется по формуле

21. Если при изменении значений х(у) случайной величины Х(Y) изменяется условное математическое ожидание M(Y|Х=х) (М(Х|Y=y)), то это математическое ожидание рассматривается как:1. действительное число; 2.вероятность значения; 3.функция регрессии Х и У (У на Х); 4.функция регрессии У на Х (Х на У ).

22. Точечная оценка неизвестных параметров генеральной совокупности должна удовлетворять свойствам:1. выражаться одним эффективным числом;2. должны задаваться ограниченным множеством;3. несмещенности и востребованности;

4. несмещенности, эффективности и состоятельности;

23. Зависимость между случайными величинами Х и У называется стохастической, если:1.они имеют общие случайные факторы, которые влияют как на одну, так и на другую случайную величину;2.они имеют неодинаковые факторы, оказывающие влияние на Х и У;3. если каждому значению случайной величины Х (У ) соответствует условное распределение случайной величины У (Х) 4. они имеют общие случайные факторы, которые влияют как на одну, так и на другую случайные величины наряду с другими неодинаковыми для обеих случайных величин факторами.