
- •Цель работы: изучение свойств простейших электрических цепей; экспериментальная проверка законов Ома и Кирхгофа в линейных электрических цепях постоянного тока. Общие сведения
- •Порядок выполнения работы
- •1. Расчёт и измерение параметров резисторного делителя напряжения
- •2. Расчёт и измерение параметров электрических цепей
- •3. Расчёт и измерение параметров моделей электрических цепей
- •Контрольные вопросы
Лабораторная работа №2
Исследование простейших электрических цепей постоянного тока
Цель работы: изучение свойств простейших электрических цепей; экспериментальная проверка законов Ома и Кирхгофа в линейных электрических цепях постоянного тока. Общие сведения
Закон Ома или соотношение между силой тока, напряжением и сопротивлением был открыт Георгом Омом в 1827 году. Закон Ома утверждает, что ток в электрической цепи прямо пропорционален напряжению и обратно пропорционален сопротивлению цепи. Это может быть выражено следующим образом:
![]()
где I - ток в амперах, U - напряжение в вольтах, R - сопротивление в омах.
Если две из этих трех величин известны, то третья всегда может быть определена. Закон Ома справедлив для любого участка цепи и может применяться в любой момент времени.
В последовательной цепи (рисунок 2.1,а) через всю цепь течет один и тот же ток:
I = IR1 = IR2 = IR3=…= IRn.
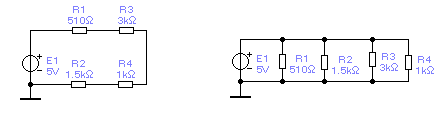
а б
Рис. 2.1. – Последовательная (а) и параллельная (б) цепи
Полное напряжение, приложенное к последовательной цепи, равно сумме падений напряжений на отдельных нагрузках (сопротивлениях) цепи:
U= UR1 + UR2 + UR3 +…+ URn.
Общее сопротивление последовательной цепи равно сумме отдельных сопротивлений цепи: R = R1 + R2 + R3 +…+ Rn.
В параллельной цепи (рисунок 2.1,б) одинаковое напряжение прикладывается к каждой ветви цепи: U= UR1 = UR2 = UR3 =…= URn.
Полный ток в параллельной цепи равен сумме токов отдельных ветвей цепи.
Величина, обратная полному сопротивлению, равна сумме обратных величин сопротивлений отдельных ветвей:
1/R = 1/R1 + 1/R2 + 1/R3 +…+ 1/Rn.
Общее сопротивление параллельной цепи всегда меньше, чем наименьшее из сопротивлений отдельных ветвей.
Первый закон Кирхгофа можно сформулировать двояко:
Алгебраическая сумма токов в узле (узловой точке) равна нулю;
Сумма втекающих в узел токов равна сумме вытекающих из узла токов.
Основой для этого закона является тот факт, что носители заряда движутся по замкнутому пути под действием э.д.с. нигде не накапливаясь в течение сколь либо продолжительного времени.
Второй закон Кирхгофа также формулируется двумя способами:
В любом замкнутом контуре алгебраическая сумма падений напряжения равна алгебраической сумме источников э.д.с., входящих в этот контур;
В любом замкнутом контуре алгебраическая сумма напряжений равна нулю.
Под напряжением в этом случае понимается как падение напряжения на компоненте схемы под действием протекающего тока, так и напряжение на выводах источников э.д.с., входящих в данный контур.
При определении неизвестных величин в цепи целесообразно придерживаться следующих правил:
1. Нарисуйте схему цепи и обозначьте все известные величины.
2. Проведите расчеты для эквивалентных цепей и перерисуйте цепь.
3. Рассчитайте неизвестные величины.
Кроме силы тока, напряжения и сопротивления, существует четвертая величина, играющая важную роль при анализе электрических цепей. Эта величина называется мощностью.
Мощность — это скорость, с которой совершается работа. Мощность расходуется только при подключении цепи к источнику. Мощность прямо пропорциональна и току, и напряжению.
Мощность измеряется
в ваттах. Ватт — это произведение
напряжения в 1 Вольт и тока в 1 Ампер.
Соотношение между мощностью, напряжением
и током может быть записано следующим
образом:
![]() , где Р - мощность в ваттах, I - ток
в амперах, U - напряжение
в вольтах.
, где Р - мощность в ваттах, I - ток
в амперах, U - напряжение
в вольтах.
Резистивные
элементы цепи потребляют мощность. Для
определения мощности, потребляемой
элементом цепи, надо умножить падение
напряжения на этом элементе на ток,
протекающий через него или воспользоваться
следующими выраженияи:
![]() или
или
![]() .
.
Полная мощность, потребляемая последовательной или параллельной цепью, равна сумме мощностей, потребляемых отдельными элементами. Это может быть выражено следующим образом:
P= PR1 + PR2 + PR3 +…+ PRn.
В любой электрической цепи должен соблюдаться баланс мощностей: алгебраическая сумма мощностей всех источников энергии должна равняться сумме мощностей всех приёмников энергии.
