
Вариант 1
Часть 1
Для матриц
 введите обозначение
введите обозначение
 ,
,
 ,
,
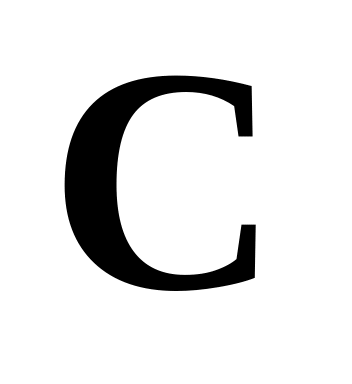 так, чтобы существовала комбинация
так, чтобы существовала комбинация
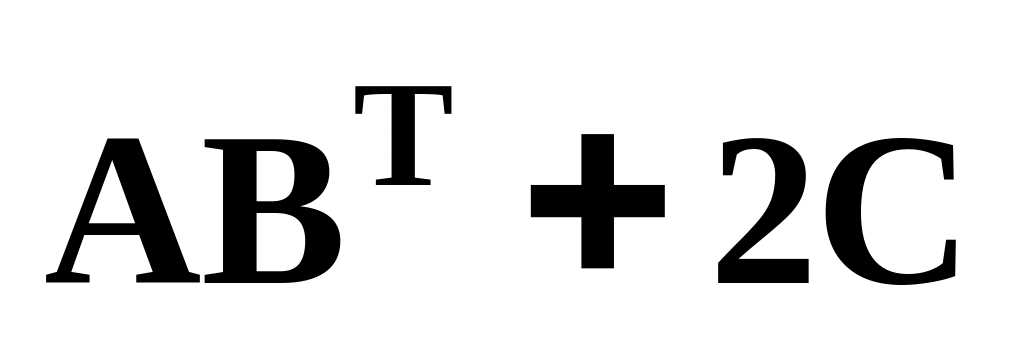 ,
и вычислите её.
,
и вычислите её.
Решить уравнение
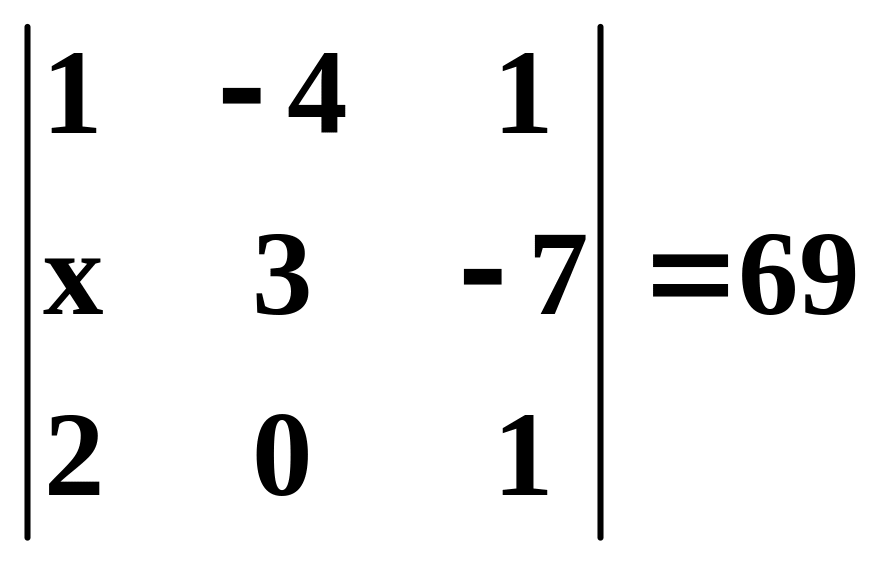 .
.
Привести к треугольному виду и вычислить определитель
 .
.
Решить матричное уравнение
![]() .
.
Решить систему а) по правилу Крамера; б) матричным методом
![]()
Решить системы методом Гаусса
а)
 б)
б)
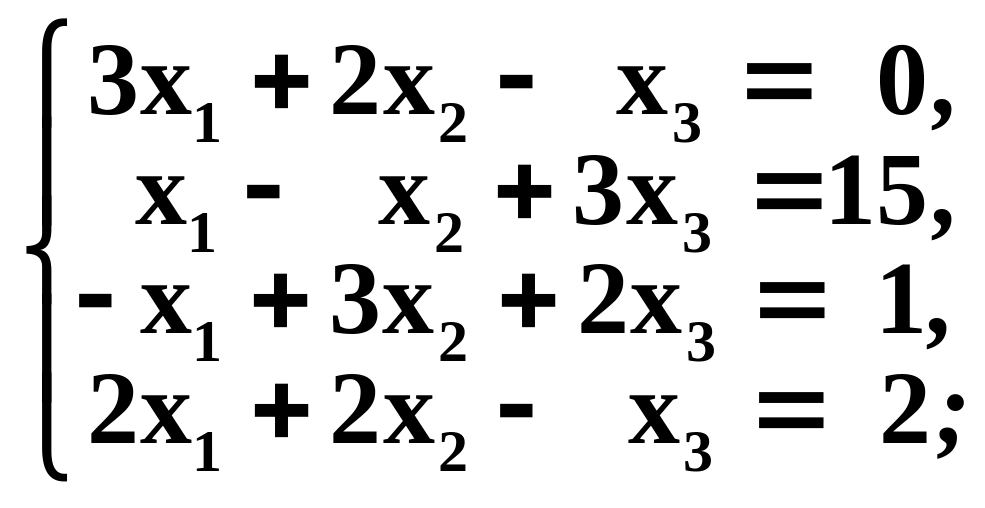
в)
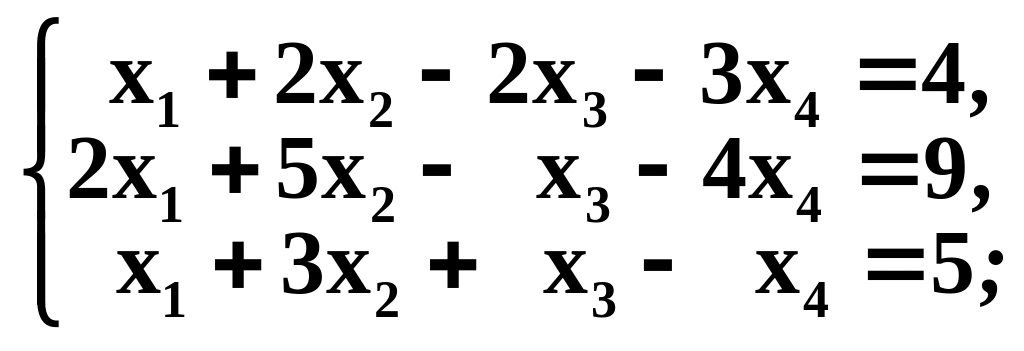 г)
г)
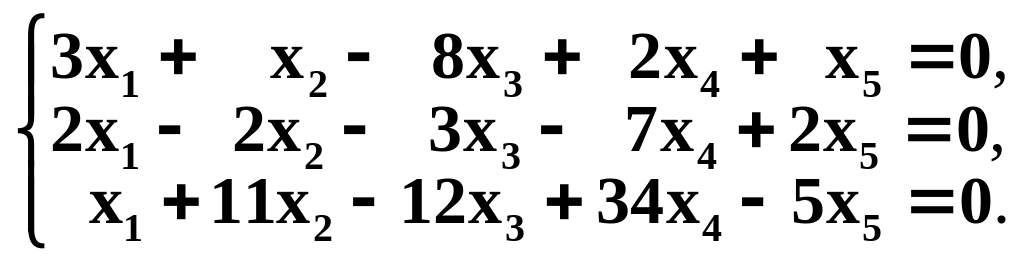
Часть 2
Проверить, коллинеарны ли векторы
 ,
если
,
если
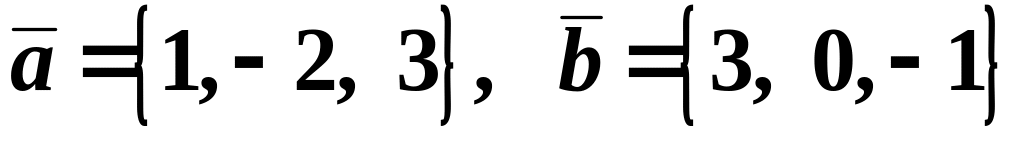 .
.Найти неизвестную координату вектора
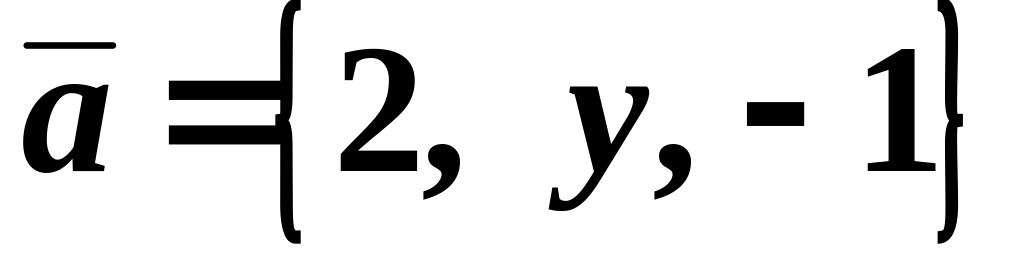 ,
если
,
если
 составляет
острый угол с осью,
одноименной неизвестной координате,
и задан модуль вектора
составляет
острый угол с осью,
одноименной неизвестной координате,
и задан модуль вектора
 .
.Найти координаты вектора
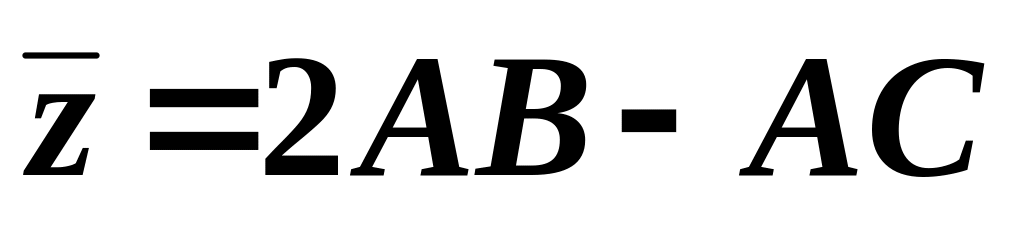 ,
если A
(–3, 4, –7),
B (1, 5, –4), C
(2, 7, –10).
,
если A
(–3, 4, –7),
B (1, 5, –4), C
(2, 7, –10).Даны координаты вершин пирамиды A1 A2 A3 A4: A1(1, 3, 6), A2(2, 2, 1), A3(–1, 0, 1), A4 (–4, 6, –3). Найти:
а)
![]() ;
;
б)
![]() .
.
Дано:
 ,
,
 ,
,
 ,
,
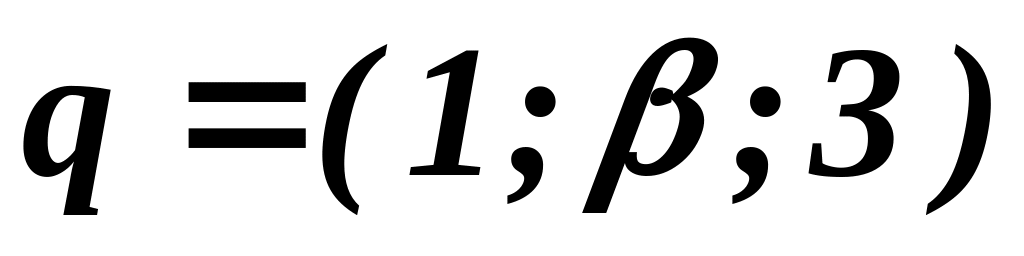 .
Вычислить:
.
Вычислить:
а)![]() ;
;
б)
![]() ;
;
в) орт вектора
![]() ;
;
г)
![]() ,
при котором вектор
,
при котором вектор
![]() перпендикулярен вектору
перпендикулярен вектору
![]() ;
;
д)
и
![]() ,
при которых векторы
и
,
при которых векторы
и
![]() коллинеарны.
коллинеарны.
Даны вершины треугольника:
 .
.
Найти:
1) уравнение стороны
![]() ;
;
2) уравнение высоты, проведенной из точки
![]() ;
;
3) уравнение медианы, проведенной из
точки
![]() ;
;
4) точку пересечения высоты
![]() и медианы
и медианы
![]() .
.
Уравнение линии второго порядка привести к каноническому виду. Определить тип кривой, сделать чертеж:
 ,
, .
.
Вариант 2
Часть 1
Для матриц
 введите обозначение
,
,
так, чтобы существовала комбинация
введите обозначение
,
,
так, чтобы существовала комбинация
 ,
и вычислите её.
,
и вычислите её.Решить уравнение
 .
.Привести к треугольному виду и вычислить определитель
 .
.
Решить матричное уравнение
![]() .
.
Решить систему а) по правилу Крамера; б) матричным методом
![]()
Решить системы методом Гаусса
а)
 б)
б)

в)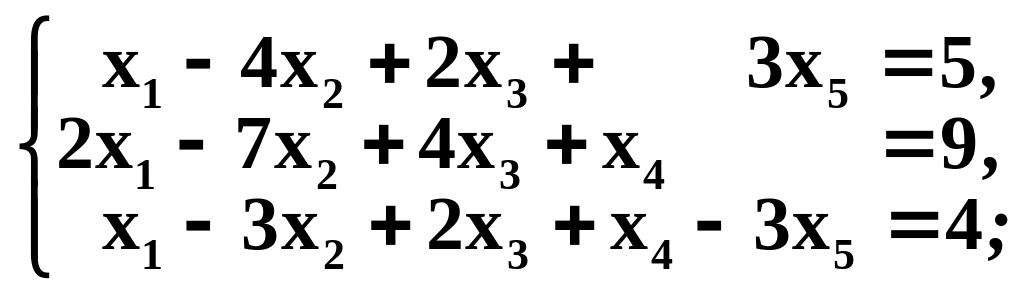 г)
г)

Часть 2
Проверить, коллинеарны ли векторы
 ,
если
,
если
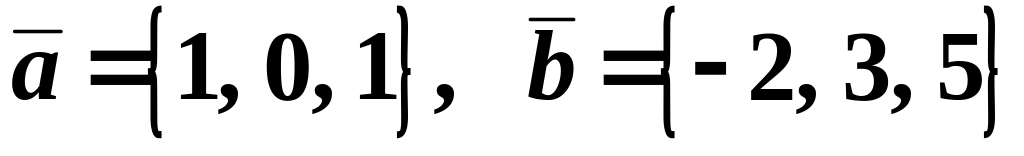 .
.Найти неизвестную координату вектора
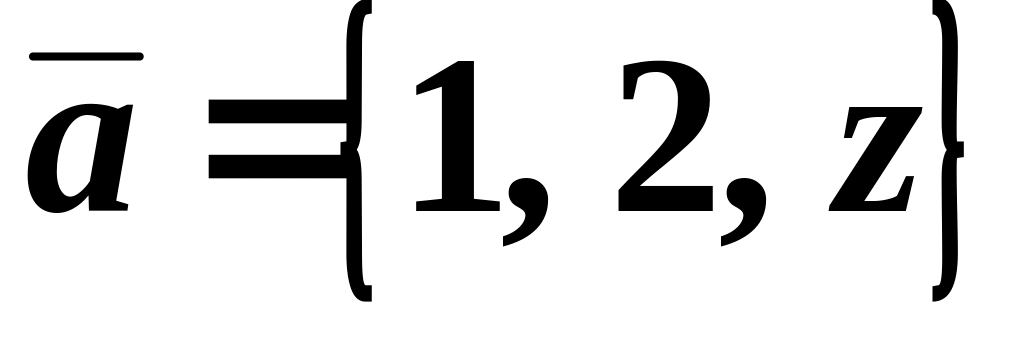 ,
если
,
если
 составляет
острый угол с осью,
одноименной неизвестной координате,
и задан модуль вектора
составляет
острый угол с осью,
одноименной неизвестной координате,
и задан модуль вектора
 .
.Найти координаты вектора
 ,
если A
(4, –2, 0),
B (1, –1, –5), C
(–2, 1, –3).
,
если A
(4, –2, 0),
B (1, –1, –5), C
(–2, 1, –3).Даны координаты вершин пирамиды A1 A2 A3 A4 : A1(–4, 2, 6), A2(2, –3, 0), A3(–10, 5, 8), A4 (–5, 2, –4). Найти:
а)
![]() ;
;
б) .
Дано:
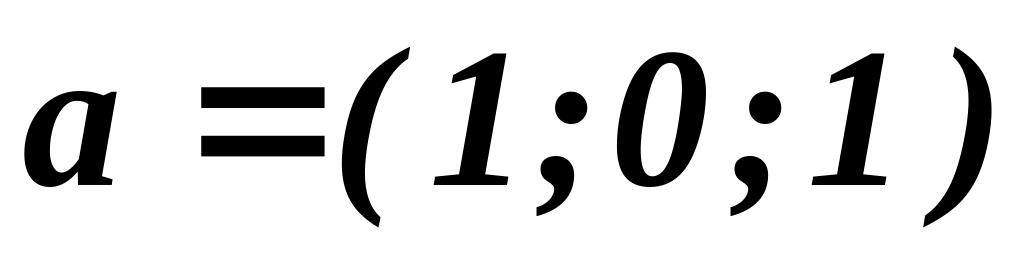 ,
,
 ,
,
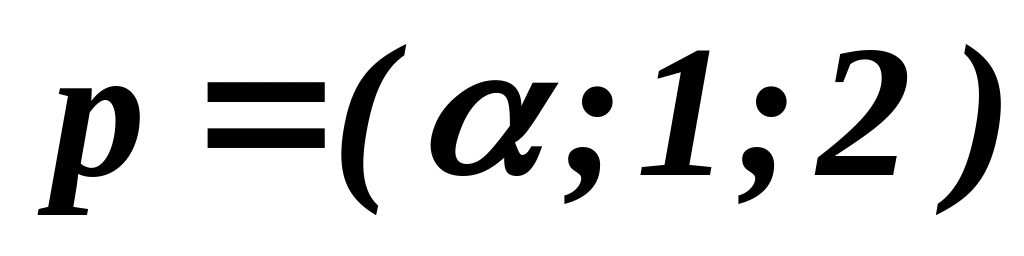 ,
,
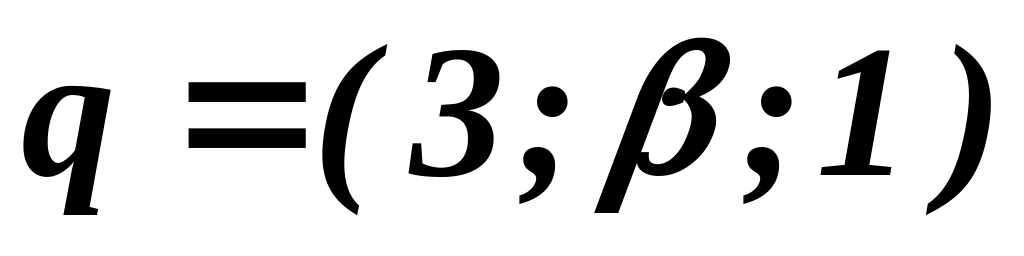 .
Вычислить:
.
Вычислить:
а) ;
б) ;
в) орт вектора ;
г) , при котором вектор перпендикулярен вектору ;
д) и , при которых векторы и коллинеарны.
Даны вершины треугольника:
 .
.
Найти:
1) уравнение стороны ;
2) уравнение высоты, проведенной из точки ;
3) уравнение медианы, проведенной из точки ;
4) точку пересечения высоты и медианы .
Уравнение линии второго порядка привести к каноническому виду. Определить тип кривой, сделать чертеж:
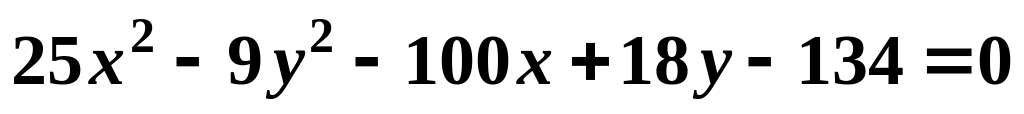 ,
, .
.
Вариант 3.
Часть 1
Для матриц
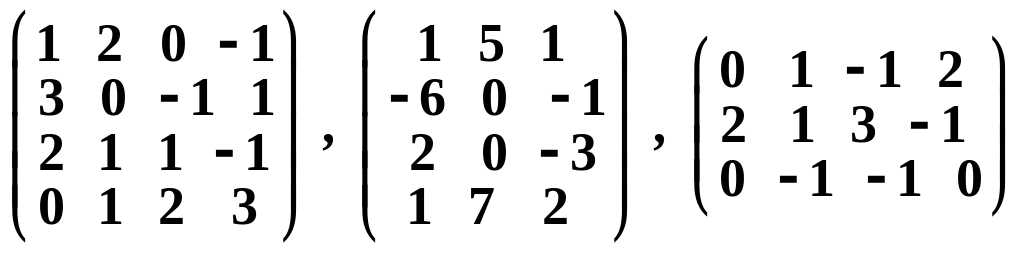 введите обозначение
,
,
так, чтобы существовала комбинация
введите обозначение
,
,
так, чтобы существовала комбинация
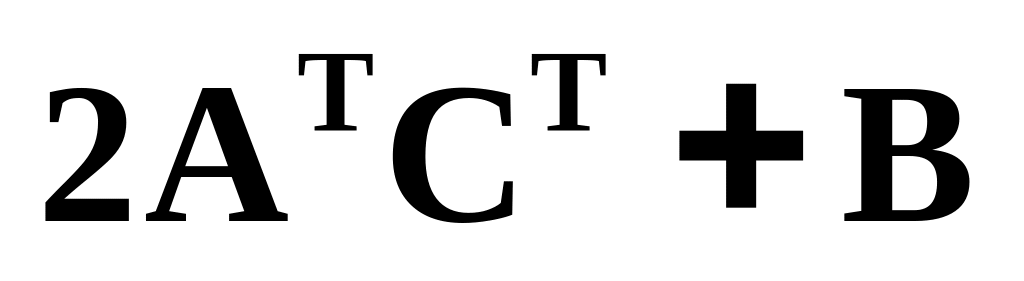 и вычислите её.
и вычислите её.Решить уравнение
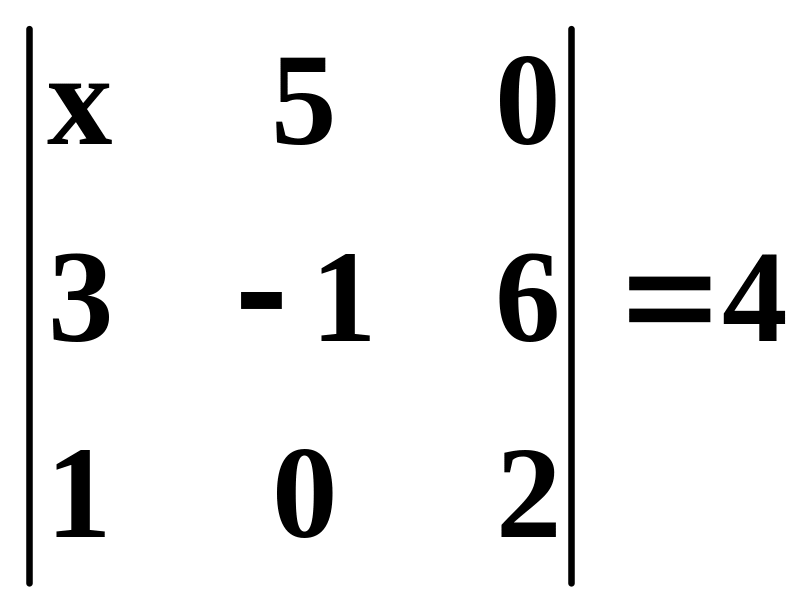 .
.Привести к треугольному виду и вычислить определитель
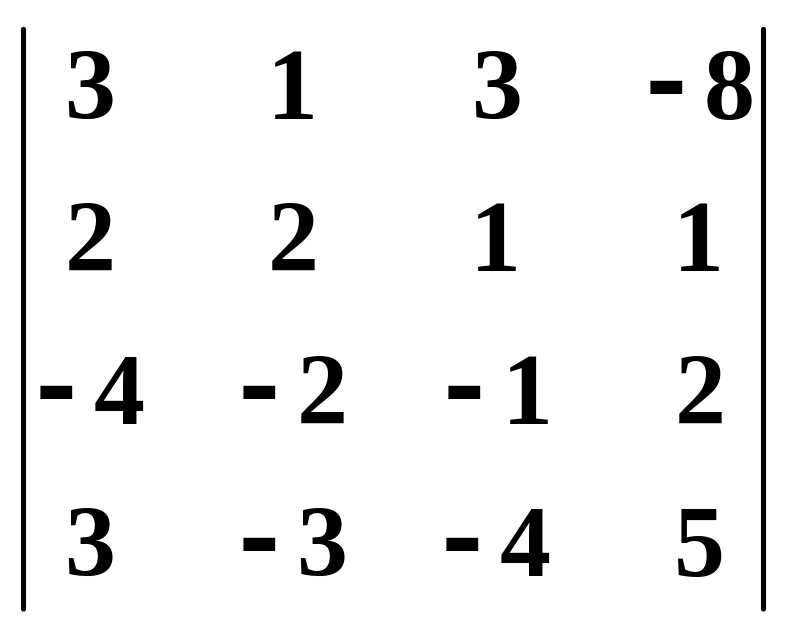 .
.
Решить матричное уравнение
 .
.Решить систему а) по правилу Крамера; б) матричным методом
![]()
Решить системы методом Гаусса
а)
 б)
б)
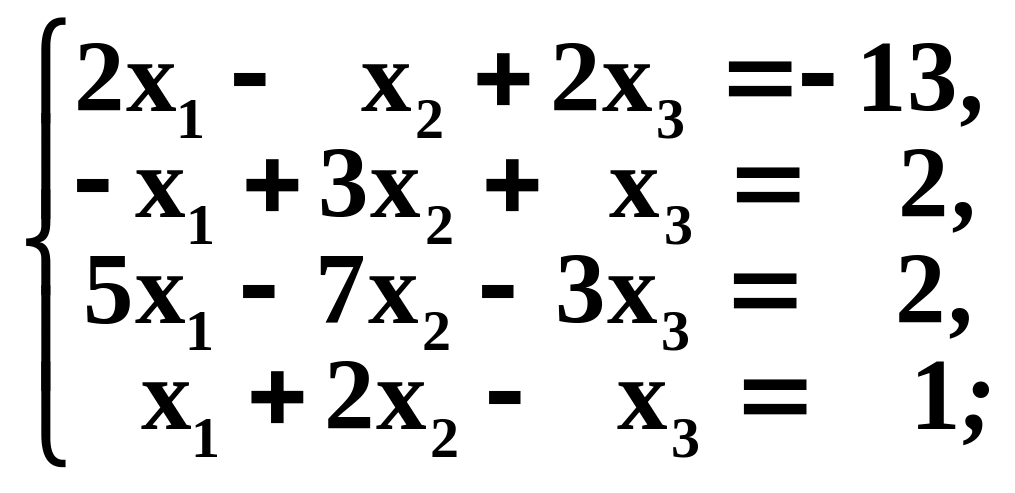
в)
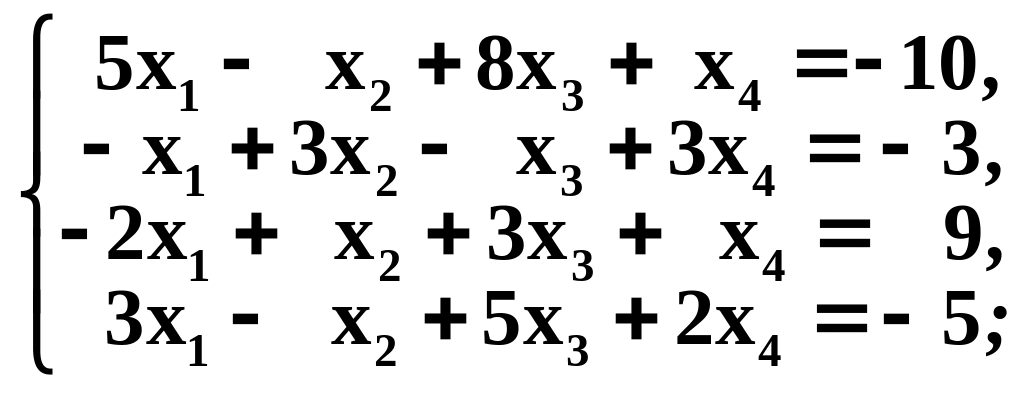 г)
г)

