1.3.2. Гомоморфизмы и изоморфизмы групп.
Определение.
Пусть
и
– группы. Отображение
называется гомоморфизмом, если для
любых
.
Определение.
Изоморфизмом
групп
называется гомоморфизм, который является
взаимно однозначным отображением. Если
группы
и
изоморфны,
то принято обозначать
.
При гомоморфизме
единица группы всегда переходит в
единицу. Действительно, если
и
– единицы групп
и
соответственно,
то
.
Умножив это равенство на
,
получим
.
Далее, при
гомоморфизме обратный к элементу
элемент переходит в обратный к
.
Действительно,
.
Аналогично,
Это и означает, что
Определение.
Пусть G
– группа с единицей e
и элемент
Наименьшее натуральное n,
для которого
называется
порядком элемента g
и обозначается o(g).
Если такого n
не существует, то считается, что
Если
–
гомоморфизм
групп, то порядки элементов
g
и f(g)
связаны, а
именно, если
то
n
делится на
m.
Действительно,
,
поэтому элемент f(g)
имеет конечный
порядок. Допустим, что n
не делится на m.
Тогда
,
где
В этом случае
что противоречит тому, что m
– наименьшая степень такая, что
Задача 1.4.1.
Определите
порядки всех элементов в следующих
группах а)
б)
в)
а)
В
группе
единицей
является элемент
Групповая операция – это сложение по
модулю 12. Порядок элемента x
это наименьшее натуральное n
такое, что
Например,
Поэтому порядок элемента
обзначаемый
равен
2. Порядки элементов
и
равны 3. Элементы
и
имеют четвертый порядок,
и
– шестой. Наконец, элементы
имеют двенадцатый порядок. Сам элемент
как и единица любой группы, имеет первый
порядок.
б), в) Решите самостоятельно.
Пример 1. Покажем,
что
Каждому преобразованию группы
можно сопоставить перестановку –
перестановку вершин треугольника ABC.
Действительно,
занумеруем вершины: A
– 1, B
– 2, C
– 3. Тогда отображение
при котором
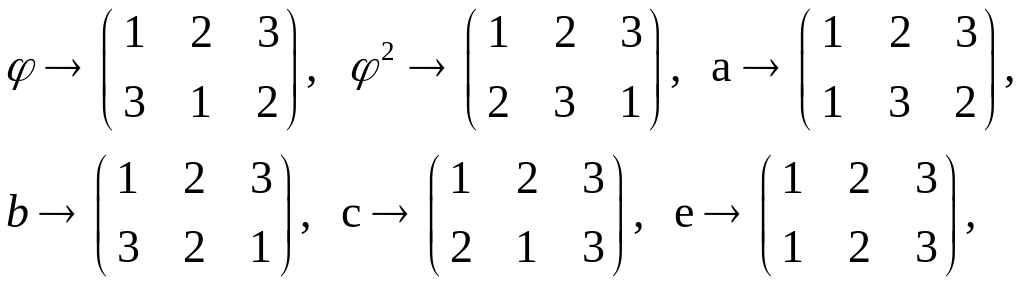
является изоморфизмом.
Пример 2.
Отображение
при котором каждому целому
ставится в соответствие его остаток
при делении на n
, является
гомоморфизмом групп, но не изоморфизмом.
Например, если
то
т.к.
Пример 3. Пусть
– группа всех действительных чисел
отличных от нуля с обычной операцией
умножения. Отображение
сопоставляет
каждой матрице ее определитель. Тогда
f
– гомоморфизм групп, т.к. определитель
произведения матриц равен произведению
определителей. Гомоморфизм f
не является
изоморфизмом, т.к. разные матрицы могут
иметь одинаковые определители.
Пример 4. Пусть
– группа всех действительных чисел с
операцией сложения, а
– группа всех положительных действительных
чисел с операцией умножения. Гомоморфизм
– определен формулой
Это действительно гомоморфизм, т.к.
Более того, этот гомоморфизм является
изоморфизмом.
Определение.
Пусть G
– группа. Нетрудно убедиться, что
множество всех изоморфизмов
также образует группу, которая называется
группой автоморфизмов группы G
и обозначается Aut
G.
Пример 5. Найдем
группу
Заметим, что в группе
каждый элемент
является суммой нескольких единиц:
Поэтому, чтобы задать гомоморфизм
достаточно задать
Действительно, если
то
и т.д.. Чтобы гомоморфизм был взаимно
однозначным отображением,
может равняться либо
либо
Обозначим первый автоморфизм
а второй –
Тогда
Поэтому
Ответы
1.4.1.б) Элементы
и
имеют
третий порядок, элементы a,b,c
– второй и
e
– первый;
в) элементы
имеют четвертый порядок, элемент (-1) –
второй и 1 – первый.