Задача 5. Проектный расчёт стержневой статически неопределимой системы при растяжении и сжатии
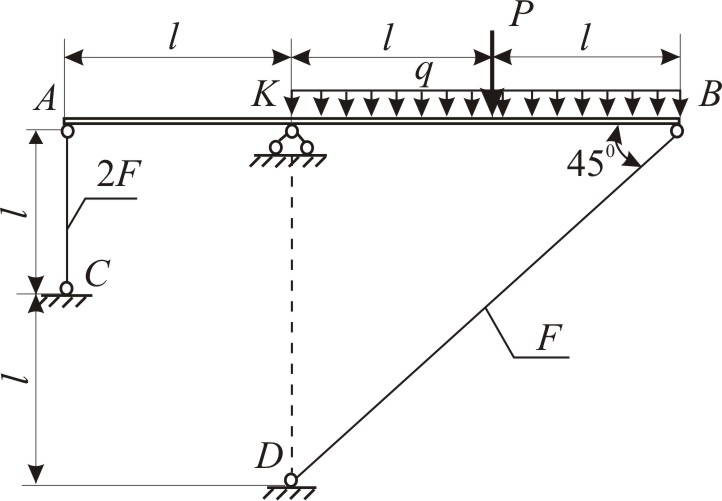
В статически неопределимой стержневой
системе абсолютно жёсткий брус AB
опирается на шарнирно-неподвижную опору
и прикреплен двумя упругими стержнями
к неподвижной опорной поверхности (рис.
1.8, а). Брус несёт нагрузку известной
величины,
,
q = 20 кН/м;
.
Требуется:
1. Найти усилия в упругих стержнях, используя уравнения равновесия и уравнение перемещений.
2. Подобрать площади поперечных сечений стержней, используя условия прочности по допускаемым напряжениям и по методу предельного состояния, если допускаемое напряжение =200МПа, предел текучести т = 320Мпа, запас прочности n = 1,6.
3. Вычислить температурные напряжения, возникающие в стержнях при повышении температуры среды на 15˚С. Принять коэффициент линейного удлинения =1,25∙10-5 1/град.
Решение
1.Нахождение усилий в стержнях.
Статически неопределимые стержневые системы – это системы, в которых количество стержней превышает количество уравнений равновесия.
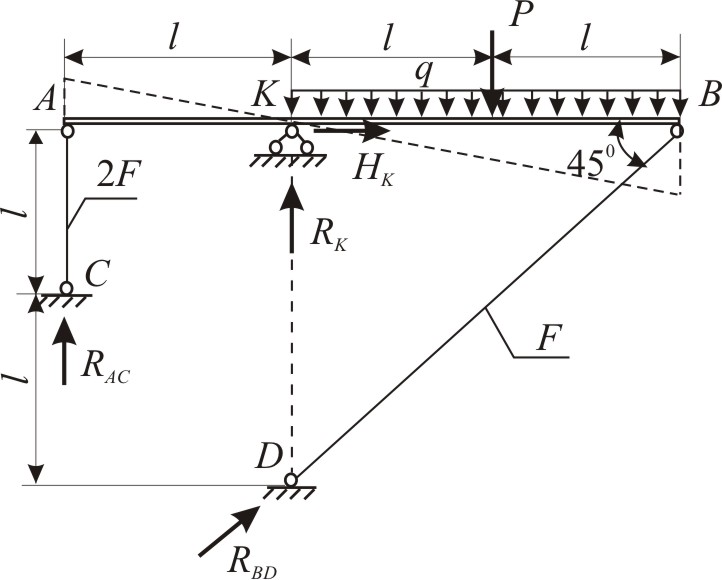
Брус АВ имеет шарнирно подвижные
опоры в точках А и В и
шарнирно-неподвижную
в точке K.
В опорах возникают реакции RAC,
RBD,
RK
и HK
(рис. 1.7,
б).
Для плоской системы можно составить
три уравнения равновесия, а неизвестных
четыре, значит, заданная система имеет
одну «лишнюю» связь, и степень ее
статической неопределимости
.
При расчётах необходимо знать продольные
силы, возникающие во всех стержнях. Для
нахождения этих усилий дополнительно
к уравнениям равновесия составляют
уравнения, учитывающие характер
деформации системы. Их называют
уравнениями совместности деформаций
(или уравнениями перемещений). Число
их равно количеству «лишних» (с точки
зрения статики) связей системы и
характеризует степень её статической
неопределимости. Использование
уравнений перемещений основано на том,
что деформации стержней можно выразить
через неизвестные продольные силы по
формуле
и сравнить между собой.
Под действием внешней
нагрузки брус АВ
займет положение
(рис. 1.7, г). Горизонтальными
перемещения концов А и В
пренебрегаем в силу малости деформаций
в таких несущих конструкциях. Отрезок
АА1 есть деформация стержня
АС, назовем её
.
На первоначальной длине стержня DВ
отложим его новую длину
(считаем, что
DВ).
Отрезок
– укорочение стержня DВ,
обозначим его
.
Из
.
Запишем связь между деформациями
и
из подобия треугольников
~
:
или
(1.19)
Выразим деформации
и
через продольные усилия, возникающие
в стержнях АС и DВ.
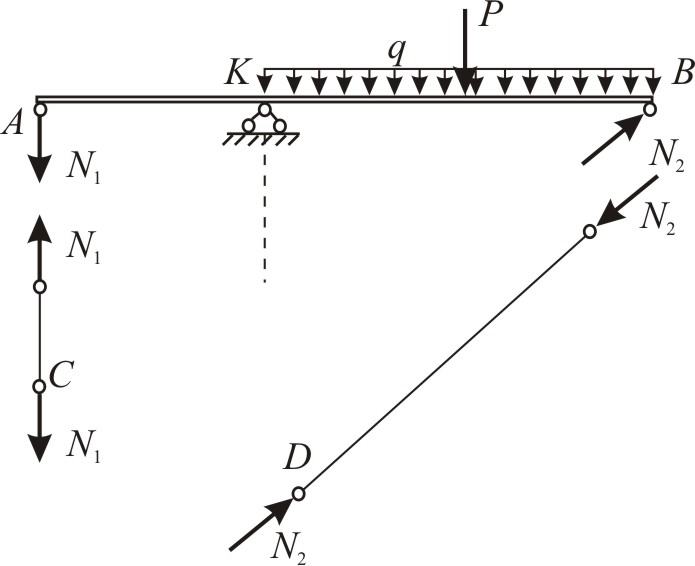
Чтобы «увидеть» эти усилия, отсечём
систему по шарнирам С и D,
а для сохранения равновесия приложим
в этих шарнирах реакции
и
(рис. 1.8, б), взяв направление в
соответствии с деформацией удлинения
и укорочения
:
усилие
покажем растягивающим, а усилие
− сжимающим. Или выполнив разрез системы
по шарнирам А и В (рис. 1.8, в),
покажем усилиями
и
воздействие разрезанных частей системы
друг на друга. Здесь хорошо видно, что
и
вызывают соответственно растяжение
и сжатие стержней. Как
известно, деформации связаны с
продольными усилиями:
и
.
Подставив эти выражения
в (1.19), получим уравнение сов-местности
деформаций в виде:
,
где
,
,
,
.
Тогда
,
и после сокращения это уравнение принимает вид
. (1.20)
Так как не требуется определить реакции в жёсткой опоре K, составим только одно уравнение равновесия ∑ мом К = 0:
или
,
.
(1.21)
Решаем систему
уравнений (1.20) и (1.21): подставив из (1.20)
в
(1.21), получим
.
Отсюда найдём
,
и по (1.20)
.
Положительные знаки
и
указывают на то, что выбранные направления
их верны.
а |
|
б |
|
в |
|
Рис. 1.8
г |
|
д |
|
Рис. 1.8 (окончание)
2. Подбор размеров сечений стержней.
Необходимые размеры поперечных сечений стержней определяют из условий прочности по допускаемым напряжениям или по предельному состоянию. В случае неодинакового сопротивления материала растяжению и сжатию условие прочности по допускаемым напряжениям имеет вид:
Для нашего примера это условие прочности по допускаемым напряжениям запишем как
или 
Отсюда получим два значения F:
и
.
Чтобы удовлетворить оба уравнения
прочности выбираем бóльшее значение
и округлив его, принимаем
,
.
Найдём величины
и
по методу предельного состояния.
При расчёте по предельному состоянию
учитываются пластические свойства
металла. Считаем, что при действии
внешних сил напряжения во всех стержнях
равны пределу текучести
,
а усилие в каждом стержне равно
.
Такое стояние системы будет предельным,
так как может вывести её из строя.
Усилия в стержнях
и
.
Выразим
и
через предельное (т. е. самое минимальное)
значение площади сечения
,
при котором и возникает предельное
равновесие:
,
.
Тогда
и
запишем как
и
.
Составим уравнение предельного равновесия, в которое войдут как внешняя нагрузка, так и усилия и . Как и выше, воспользуемся уравнением ∑мом К = 0, оно принимает вид:
Отсюда найдём предельное значение
.
Допускаемые значения площади сечения
стержней
,
при которых система будет безопасной,
можно найти, используя коэффициент
запаса прочности n:
увеличиваем полученное значение
в n раз, т. е.
.
В нашем случае
.
Тогда принимаем площади сечений
и
.
Как и следовало ожидать, эти
величины F
получились меньше, чем по методу
допускаемых напряжений.
3. Вычисление температурных напряжений.
Найдём напряжения
,
появляющиеся при повышении температуры
среды на 15ºС. В статически неопределимых
системах с повышением температуры
окружающей среды уже при отсутствии
внешней нагрузки возникают напряжения,
так как каждый стержень стремится
удлиниться на величину
,
а этому препятствует другие стержни и
опоры системы (рис. 1.8, д). В результате
в стержнях возникают продольные усилия
.
Здесь деформация каждого стержня
слагается из температурной
и деформации, полученной от возникающего
продольного усилия
и равной
,
т. е. деформация стержня
.
Методика определения усилий и напряжений остается прежней, как и при нахождении усилий N и напряжений от внешней нагрузки.
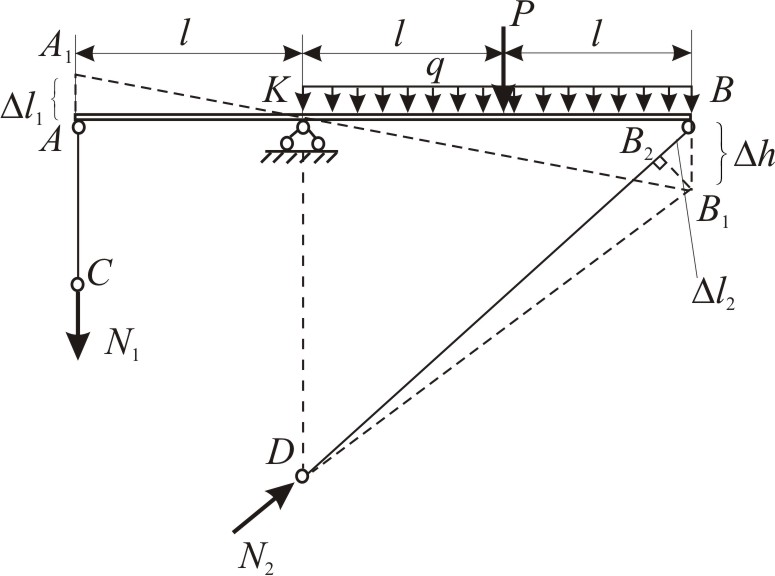
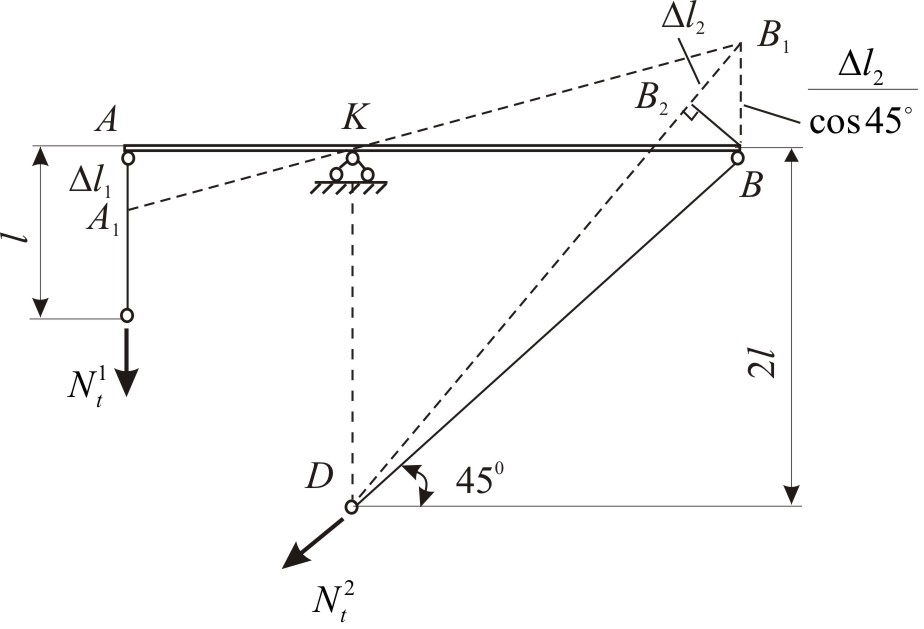
Пусть при повышении температуры брус
АВ займет положение А1В1.
Тогда стержень АС получит сжатие
на величину
=АА1,
а стержень DВ -
растяжение на
=ВВ2
(рис. 1.8, д). Предположим направление
усилий
и
растягивающими и запишем деформации
стержней:
,
.
Уравнение равновесия ∑мом К = 0 и уравнение перемещений образуют систему следующих уравнений:
Отсюда вычисляем температурные усилия
,
.
Как видно, стержни АС и DВ испытывают сжатие, при котором возникают температурные напряжения
,
.