2.Эйлерова характеристика многоугольников

Определение: Многоугольником называется плоская фигура М, состоящая из

объединения конечного числа выпуклых многоугольников так, что выполнены следующие два условия:

Любые два выпуклые многоугольника либо совсем не имеют общих точек, либо имеют только общую вершину, либо имеют общую сторону.

Фигура М связна, т.е. любые две её точки можно соединить простой незамкнутой ломаной, целиком лежащей в М.

Под разбиением многоугольника на клетки следует понимать, что гранями разбиения будем называть те выпуклые многоугольники, из которых составлен многоугольник М, ребра-стороны этих выпуклых многоугольников, вершины разбиения-их вершины.

Определение: Многоугольник называется простым, если его граница состоит из одного контура

Теорема [1,стр25]

Эйлерова характеристика простого многоугольника равна 1 . Без доказательства.

3.Формула Эйлера для выпуклых многогранников Теорема [1,стр45]

В-Р+Г=2 для всякого выпуклого многогранника.

Доказательство: Предположим что все его вершины расположены на разной

высоте и занумерованы в таком порядке V,, V„ чтобы каждая следующая

была выше предыдущей. Обозначим через Г,(і=1,....,В-1) число граней многогранника, для которых точка V, является самой нижней вершиной или, другими словами, которые "выходят" из вершины V,.

Через Р,( і=1 ,В-1) обозначим число ребер многогранника, которые

имеют вершину V,, своим нижним концом.

Так как к вершине V, примыкает одинаковое число ребер и граней, и все они "выходят" из нее вверх, тоР,=Г,.

Рассечем теперь многогранник X горизонтальной плоскостью Q , расположенной чуть выше вершины V,. В сечении получится выпуклый многоугольник М,.

Каждому их Р ребер многогранника, выходящиму вверх из точки V,, соответствует своя вершина М,. Аналогично, каждой из Г, граней, выходящих вверх из этой же точки, соответствует своя сторона многоугольника М,.

Названные вершины и стороны образуют простую (незамкнутую) ломаную линию (возможно состоящую только из одной вершины). Так как Эйлерова характеристика такой ломаной равна 1, то Р,-Г,=1

(i=2,....,B-l).

Общее число ребер многогранника равно Р= Р,+....+ Р е_,, а общее число граней равно Г=Г,+...+ Г,_,

Следовательно В - Р + Г =В-( Р,+....+ Р „.,)+( Г.+...+ Г,_,)=В-( Р,+....+ Р,.,)+ Р, +(Р,-1)+...+ (Р „., -1 )=В-( Р,+....+ Р „_,)+( Р,+....+ Р, )-(В-2)=2

Теория групп Определение: Множество с операцией сложения +: GxG-»G называется группой, если

Va,b,c е G (a+b)+c = а+(Ь+с)

3 Г OeG т.ч. VaeG а+0 = 0+а=а

V aeG 3(-а) eG, т.ч а+(-а) =(-а)+а=0

Если кроме того выполнено условие коммутативности: 4) Va,B eG a+b = b+a то G называется абелевой группой. Далее в нашей работе мы рассматриваем только абелевы группы. [5,стр28]

Определение: Н сС Н называется подгруппой G, если

V Џ,,Џ, € Н => Џ,+ Џ, 6 II

V h е Н=> (-Џ) € Н Определение: Левым смежным классом G по подгруппе Н с

представителем а называется множество = { а + Џ, где h е Н } которое обозначается а + Н

Если G- абелева, то для любой подгруппе Н можно определить новую групп) называемой факторгруппой и обозначаемой G/H. Элементами G/H являются левые смежные классы G по Н с операцией сложения: (а+ H)+(b+H) (а+Ь)+Н Пример: Множество целых-Z является абелевой группой относительно обыкновенного сложения. Подгруппами Z будут множества nZ={ пх, где xeZ | где n-какое-то фиксированное натуральное число. В данном случае факторгруппой будет множество остатков от деления на п, с операцией сложения и взятия от полученного числа остатка от деления на п.

z/nz={ о,т, }

а ,Ь е Z/nZ а +Ь =а + Ь

Говорят, что абелева группа G допускает конечную систему образующих х,,х;,...,х, если каждый элемент xeG может быть записан в виде п,х,+...+п,х, где n,,...,n, eZ.

В нашей работе мы будем пользоваться без доказательства двумя фактами. Первый факт:(Теорема о конечнопорожденных абелевых группах) Всякая абелева группа G с конечным числом образующих представляется прямой суммой циклических групп:

,...,Ar; В,,...,В? , где A,=Z і = Ц

= Z/Xjz ~ Причем Tj4l делится на тг

Число г называется рангом группы G , a iJ г - коэфицентами кручения.

Второй факт: (Теорема о ранге групп)

panrG рангО/Н t рангН G-абелева группа [4,стр66]

Симплекс

Определение а„. а,, а,, а,- система независимых точек пространства R А' ={х eR|х= Х0а0+Х,а,+ Х2а, +Х,а,Д„ +Х.+ Х. +Х,=1 и X, г ОД, г О, X. гО и X, г 0} называется 3- мерным симплексом. Будем писать А' =( а„. а,. а,. а,)

Исходные точки а„, а,, а., а, называются вершинами симплекса А ' Говорят, что симплексы А и В эвклидова пространства R 1 расположены правильно, если они или вовсе не пересекаются или их пересечение А пВ является гранью каждого из симплексов А и В. Одномерными гранями А являются: (а„ ,а,),( а„.а,).( а0.а,).( а, ,а .),( а ,,а,),( а ,.а,) Двумерными гранями А являются: (а'.а,,а,), (а,„а,.а,), (а (,.а ,,а,), (а, .а ..а,) [2,стр23]

Комплекс

Определение: Конечная совокупность К симплексов называется комплексом , если:

Наряду с каждым симплексом А совокупность К, в К входит также и любая грань симплекса А

Каждые два симплекса К расположены правильно[2,стр27]

1.Подкомплекс Определение: Подкомплекс комплекса К называется всякий комплекс L , все симплексы которого принадлежат К.

2 .Связность

Определение: Комплекс К будем называть связным, если его невозможно разбить в сумму двух не пустых подкомплексов L и М без общих симплексов.

Теорема

К связен о Для каждых его двух вершин а и е существует последовательность вершин а,=о, а,, причем две соседние вершины этой последовательности служат вершинами одномерного симплекса из К

Доказательство: Допустим, что К не связен и потому распадается в сумму двух непересекающихся подкомплексов L и М. Пусть а- вершина из L, е вершина из М. Если цепочка существует для этих вершин . Через а, обозначим последнюю ее вершину , принадлежащую L. Существующий симплекс (а, ,а) не может принадлежать ни L , ни М.

Обратно, пусть К связен. Зафиксируем какую-либо его вершину а и рассмотрим множество Е всех таких вершин е комплекса К, которые можно связать с а цепочкой. Очевидно, что если симплекс А имеет хоть одну вершину, принадлежащую Е ,то и все вершины его принадлежат Е. Совокупность всех симплексов из К, имеющих вершины в е , составляет подкомплекс L. Множество всех симплексов из К, не принадлежащих L , составляет подкомплекс М из К, и потому пусто ввиду связности К. [2,стр49].

Определение: Компонентом некоторого комплекса К будем называть такой связный его подкомплекс L, что К расподается в сумму двух пересекающихся подкомплекс М и L.

1,2- примеры комплексов 3,4,5- не комплексы

Оператор границ d(ao,a, ..••ar)=S~1)'(ao,ai....ar-i,ar + i.ar [6,стр51]

Числа Бетти Комплекса

Теорема

Пусть К,,..„К, - совокупность всех компонент комплекса К.

Пусть В;, - группа Бетти комплекса К, В; - группа Бетти комплекса К,, то

в'=в;®в;љ...®в;,

Доказательство: Пусть L'- группа всех г- мерных цепей комплекса К. Через L; обозначим ее подгруппу, составленную из всех цепей в которые с коэффициентом входят лишь симплексы комплекса К,.

L'=L[®...®L; ПустьHr'=dL;-' => н-'-нг1®...©Н? Z;={xЈ L;|dx=0} Пусть z=x,+...+x,

0=dz=dxl+...+dxp ,=(),...,dx(, =0,следовательно Z'=Z\®...®Z'p

Z' / 7' / Z' /

Следовательно '/„,= 7„,®-® 7„, [2,стр54]. /Я /«, /не

Пусть A°,...,A° -совокупность всех его положительно ориентированных нульмерных симплексов А°= +(а,) x=g, A°+...+ga А°-произвольная цепь из К Индекс I(x)= g,+...+ g0. Очевидно, что 1(х+у)= 1(х)+ 1(у). Если 3 у, что x=dy=> 1(х)=0

Для связного комплекса К условия 1(х)=0 и x=dy эквивалентные. Сверх того Bg(K) изоморфна G. Пусть а не- две произвольные вершины из К . Предположим А; = +(а ,,а„,). Рассмотрим цепь y=gA \ +gA J+.. ,+gA \, dy=gE°-gA°.

Из этого выходит , что произвольная нульмерная цепь х гомологична цепи gA°. Так как х и gA° гомологичны, то индексы их равны => I(x)= g х~ 1(х) А" =.если 1(х)=0 , то x=dy. Следовательно, верна теорема.

Теорема: I Іульмерная группа Бетти произвольного комплекса К по полю коэффициентов G изоморфна прямой сумме нескольких экземпляров группы G, причем число этих экземпляров равно числу компонент комплекса К. [2,стр52]

Доказательство: Для связного комплекса оператор х-» 1(х) дает гомолорфное отображение L°=Z° в группу G.

Так как при произвольном ge G имеется в Z" цикл gA°, индекс которого равен g э I(Z")= G.1^ 1= Н" ^ zy = G

Формула Эйлера- Пуанкаре Теорема: Пусть К 3-мерный комплекс. Число г- мерных симплексов комплекса К обозначим через а', г- мерное число Бетти обозначим через р'.

Тогда /(К)= £(-1)'аг =£(-1)'/?' •

Число /(К) называется эйлеровой характеристикой комплекса К. Доказательство: Обозначим Г-группу порожденную г- мерными симплексами комплекса К. Тогда ранг L'=a'. ранг £'= рангг'+ ранг L'/Z' Ј'/Z' и Н' '- изоморфно, следовательно ранг U= ранг2'+ ранг Я'"1

ранг Г =ранк Н' + ранг Z' / Н' = ранг Н' + Р'. Предположим ранг Н'1 =0 , следовательно а'- рг + ранг Н' + ранг/Г"' , следовательно

t(-l)'«'=t(-0'/9r ■ [2,стр55]

Вычисление чисел Бетти для некоторых комплексов Пример 1.

0: (0), (1) d(0)=d(l)=0 1: (01) d(01)=(l)-(0) /?0 =1 д= о рг= о р,= о

Пример 2

d(0)=d(l)=d(2)=0 d(01)=(l)-(0) d (02)= (2)-(0) d(12)=(2)-(l) d ((01)+ (02)+ (12))=0

0: (0), (1), (2)

1: (01), (02), (12) Л, =1 Д= 1 /Sj=0 A=0

Пример 3.

d (0)= d (1 )= d (2)=0 d (01)= (l)-(0) d (02)= (2)-(0) d (12)= (2)-(l)

0: (0), (1), (2) d(012)=-(02)+(01)+(12) 1: (01), (02), (12)

2: (012) p„ =1 p,=0 fi,=0 A=0

Пример 4.

0: (0), (1), (2), (3) 1: (01), (02), (12), (03), (23), (13) 2: (012), (031), (132), (032) 3: (0123)

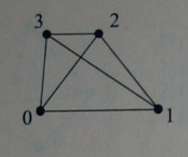
0: (0), (1), (2), (3) d

1: (01), (02), (12), (03), (23), (13) d 2: (012), (031), (132), (032) d

d d

A =1 4-6+4= p0- Л+ A A

2=1- Д+ А A

Пример 5.

Д, =1 Д =0 рг=О Д=0

d(0)=d(l) d(2) d(3) 0

d (01) = (l)-(O) d(03) = (3)-(0) d (02) = (2)-(0) d (23) = (3)-(2) d (12) = (2)-(l) d(13) = (3)-(l)

d (012) = (12)-(02)+(01) d(031) = (31)-(01)+(03) d (132) = (32)-( 12)+( 13) d (032) = (32)-(02)+(03) d ((132)- (032)+(012)+(031 ))=0

fl= 1 p = 0

A =1 д= О A=1 A=0

d(0)=d(l)=d(2)=d(3)=0 d (01) = (l)-(O) d(03) = (3)-(0) d (02) = (2)40) d (23) = (3)-(2) d (12) = (2)-(l) d (13) = (3)-(l)

d (012) = (12)-(02)+(01) d (031) = (31)-(01)+(03) d (132) = (32)-( 12)+( 13) d (032) = (32)-(02)+(03) d (0123) = (123)-(023)+(013)-(012)

0: (0),(О, (2), (3), (4)

1: (01), (02), (03), (13), (12), (23), (14), (24), (34) 2: (012), (031), (023), (123), (124), (234), (134) 3: (0123), (1234)

5^5-9+7-2=1=/»,- /»,+ Рг-Р>

А=1, А= 0

d(0123)= (123)4023)+ (013Н012) — (012)= (123)-(023)+ (013)- d(0123) d( 1234)= (234)- (134)+ (124)-(123) — (123)= (234)- (134)+ (124)- d(1234)

(012)= (234)- (134)+ (124)- (023)+ (013)- d(0123)- d(1234) z=a(012)+P(031 )+у(023)+а( 123)+b( 124)+c(234)+d( 134)

dz=0= a( 12)-a(02)+a(01)+P(31)-P(01)+P(03)+ +7(23)-у(03)+7(02)+а(23)-а( 13)+а( 12)+ +b(24)-b(14)+b( 12)+c(34)-c(24)+c(23)+ +d(34)-d(14)+d(13)

a+a+b=0 6) y+a+c=0

-a+7=0 7) b-c=0

a-P=0 8) -b-d=0

p +a-d=0 9) c+d=0

p-y=0

a =Р=њ a+a+b=0 a+a+b=0 "l b=c=-d P+a-d=0 a+a-d=0 [■ a=-a-b

њ+а+с=0 a+a+c=0 J

z= a(012) + a (031) + a(023)-(a+b)(123)+b(124)+b(234)-b(134) z= a(012) + a (031) + a(023)-a( 123) + b( 124) +b(234)-b( 134)-b( 123)= = a(012) + a (031) + a(023)-a( 123) + bd( 1234)= = a(012)-a (013) + a(023)-a(123) + bd(1234) = =-ad(0123)+bd( 1234)

A=0, 1=1-Д+0-0 c=> p=Q

Пример 6.

A=1 A=0 p,=Q д=0

Заключение

Наш проект посвящен доказательству формул Эйлера для основных геометрических фигур, где вводится понятие Эйлеровой характере™ки.

Эйлерова характеристика играет важную роль в разделе математики, называемой комбинаторной топологией. Мы разобрались с основами теории групп и используем две фундаментальные теоремы, теорема о структуре конечнопорожденных абелевых групп и теория о ранге группы, подгруппы и факторгруппы. Также мы вводим понятие симплекса и комплекса и используем оператор взятия границы.С помощью данной теории вводим числа Бетти и доказываем топологическую инвариантность эйлеровой

2