
- •1. Переведення чисел із однієї позиційної системи числення в іншу
- •1.1. Алгоритм безпосередньої заміни
- •2.2. Переведення цілих чисел з системи числення з основою q в систему числення p
- •2.3. Переведення дробових чисел
- •2.4. Точність переведення дробових чисел з системи числення з основою q в систему числення p
- •2.5. Переведення чисел із однієї системи числення в іншу у випадку
- •2.6.1. Переведення чисел у симетричні і кососиметричні системи
- •2.6.2. Переведення чисел із симетричних і кососиметричних
- •2.6.3. Переведення чисел у неканонічну двійкову систему
- •2.6.4. Переведення з неканонічної двійкової системи у канонічну
- •Рекомендується виконати домашнє завдання 10.
- •2.7. Системи числення з від’ємними основами
- •2.7.1. Переведення цілих десяткових чисел у мінус-двійкову
- •2.7.2. Переведення дробових десяткових чисел у мінус-двійкову
- •2.7.3. Переведення змішаних дробових десяткових чисел у
- •2.8. Переведення двійкових чисел у мінус-двійкову систему
- •2.8.1. Переведення додатних двійкових чисел у мінус-двійкову
- •2.8.2. Переведення від’ємних двійкових чисел у мінус-двійкову
- •2.8.3. Перехід від додатного числа, заданого в мінус-двійковій системі числення до від’ємного і навпаки
- •2.8.4. Переведення чисел з мінус-двійкової системи числення
- •2.9. Переведення чисел з десяткової системи числення в сзк з використанням властивостей залишків
- •2.10. Метод ортогональних базисів переведення чисел з сзк
- •Рекомендується виконати домашнє завдання 15.
- •2.11. Переведення чисел з сзк в десяткову систему числення
- •2.12. Питання для самоконтролю
- •2.13. Завдання для практичної роботи
- •2.14. Завдання для самостійної роботи
- •Додатки
Переведення чисел із однієї системи числення в іншу
Тема: ПЕРЕВЕДЕННЯ ЧИСЕЛ ІЗ ОДНІЄЇ СИСТЕМИ
ЧИСЛЕННЯ В ІНШУ
Мета заняття: Вивчити основні алгоритми переведення чисел з однієї системи числення в іншу та набути відповідні практичні навички.
1. Переведення чисел із однієї позиційної системи числення в іншу
Необхідність в переведенні чисел із однієї системи числення в іншу виникає зажди, коли в цифровій обчислювальній машині (комп’ютері) використовується система числення, відмінна від тієї, в якій задані вихідні дані або в якій системі числення потрібно одержати результат. Слід відмітити, що алгоритм переведення чисел із однієї системи числення в іншу істотно залежить від самих систем числення. Тому, з метою конкретності, спочатку розглянемо випадок, коли задане число А представляється в позиційній однорідній системі числення вигляду
![]() , (2.1)
, (2.1)
а його кількісний еквівалент обчислюється за формулою
![]() , (2.2)
, (2.2)
Переведення
заданого числа здійснюється в позиційну
однорідну систему числення з основою
![]() .
.
Розглянемо основні типи методів переведення чисел із однієї позиційної системи числення в іншу.
1.1. Алгоритм безпосередньої заміни
Один з найбільш загальних алгоритмів переведення чисел визначається правою частиною виразу, що задає правило обчислення кількісного еквівалента числа, записаного у формі (2.2).
Для
переведення числа А,
заданого в системі числення з основою
р,
в систему з основою q,
необхідно записати А
в
формі для обчислення кількісного
еквівалента (2.2), далі замінити цифри
![]() і основу р
їхніми еквівалентами в системі з основою
q,
a потім обчислити отримане зображення
за правилами арифметики в системі з
основою q.
і основу р
їхніми еквівалентами в системі з основою
q,
a потім обчислити отримане зображення
за правилами арифметики в системі з
основою q.
Приклад 2.1. Перевести двійкове число А2=1101,0101 в десяткову систему числення.
Розв’язання. Використавши формулу (2,2), одержимо
![]()
![]() .
.
Викладений
алгоритм переведення чисел з однієї
системи числення в іншу одержав назву
алгоритму
безпосередньої заміни.
Цей
алгоритм зручно використовувати у
випадку, коли
![]() ,
причому q
відповідає
системі числення, де просто і "звично"
виконуються операції додавання і
множення (наприклад, у десятковій
системі). Для спрощення обчислень при
цьому можна побудувати алгоритм обчислень
за так званою схемою
Горнера,
якій у даному випадку відповідає вираз,
який легко одержується з формули для
кількісного еквівалента числа шляхом
багаторазового винесення за дужки:
,
причому q
відповідає
системі числення, де просто і "звично"
виконуються операції додавання і
множення (наприклад, у десятковій
системі). Для спрощення обчислень при
цьому можна побудувати алгоритм обчислень
за так званою схемою
Горнера,
якій у даному випадку відповідає вираз,
який легко одержується з формули для
кількісного еквівалента числа шляхом
багаторазового винесення за дужки:
![]()
![]() .
.
Звідси видно, що алгоритм безпосередньої заміни, власне кажучи, складається з двох алгоритмів, а саме: переведення цілого числа, виконуваного відповідно до рекурентної формули:
![]()
де
![]() -
ціла частина вихідного числа в системі
числення з основою q;
і переведення дробів за рекурентною
формулою
-
ціла частина вихідного числа в системі
числення з основою q;
і переведення дробів за рекурентною
формулою
![]()
де
![]() -
дробова частина вихідного числа в
системі з основою q.
З наведених рекурентних формул випливає,
що для одержання
-
дробова частина вихідного числа в
системі з основою q.
З наведених рекурентних формул випливає,
що для одержання
![]() необхідно
виконати n+1
кроків обчислень, а для одержання
необхідно
виконати n+1
кроків обчислень, а для одержання
![]() -
-
![]() кроків.
кроків.
На
лістингу 1 наведено програму MBZ_c_p_10_Ch(X,
p),
реалізовану з використанням засобів
пакету Mathcad,
яка реалізовує
алгоритм
безпосередньої заміни з використанням
схеми
Горнера для переведення цілих чисел з
системи числення p
![]() в десяткову систему. Тут
X
задане
ціле число,
а p
– основа числення, в яку потрібно
перевести задане число Х,
На цьому ж лістингу наведено приклади
переведення при різних значеннях p.
При цьому результати виводяться як у
звичайному вигляді (число А),
так і вигляді вектора (вектор Av),
компонентами якого є цифри вихідного
числа X.
в десяткову систему. Тут
X
задане
ціле число,
а p
– основа числення, в яку потрібно
перевести задане число Х,
На цьому ж лістингу наведено приклади
переведення при різних значеннях p.
При цьому результати виводяться як у
звичайному вигляді (число А),
так і вигляді вектора (вектор Av),
компонентами якого є цифри вихідного
числа X.
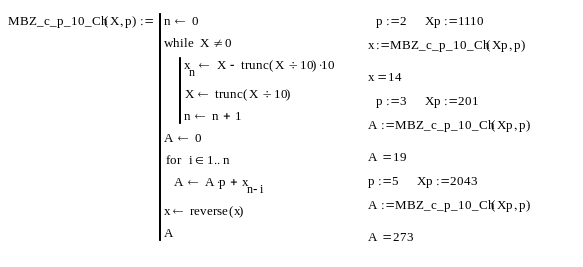
На лістингу 2 наведено програму MBZ_d_p_10_Ch(X,p,m), яка реалізовує схему Горнера для переведення дробових чисел методом безпосередньої заміни з системи числення p в десяткову систему точно або з одержанням m розрядів дробової частини. Робота програми ілюструється прикладами. Результати виводяться як у звичайному вигляді (число В), так і вигляді вектора (вектор Вv), компонентами якого є цифри вихідного числа X.

На лістингу 3 наведено програму MBZ_ p_10(X,p,m), яка реалізовує алгоритм для переведення змішаних чисел з використанням схеми Горнера з системи числення p в десяткову систему з одержанням m розрядів дробової частини. У цьому випадку спочатку виділяється ціла і дробова частини заданого числа, потім здійснюється переведення цілої і дробової частин і виведення цілої, дробової частин і одержаного числа. Робота програми ілюструється прикладами.

На лістингу 4 наведено програми переведення цілих і дробових десяткових чисел з десяткової системи числення в систему числення з основою р із виведенням результатів у векторній формі. Це дає можливість переводити десяткові числа і в 16-ву систему числення із одним недоліком, що шістнадцяткові числа виводяться в десятковій системі числення. Зауважимо, що при виведенні результатів дробових чисел розряди з нулями в кінці числа не виводяться.

