1) Точечные оценки параметров a0; a1, ;

2) Найти 95% доверительные интервалы для параметра a1 уравнения регрессии и для параметра ;

3) среднюю добычу угля на одного рабочего для пласта мощностью 20 м;

4) найти 95% доверительные интервалы для средней и индивидуальной выработки рабочего для пласта мощностью 20 м;

5) проверить гипотезу о значимости уравнения регрессии на уровне значимости =0.05;

6) определить коэффициент детерминации регрессионной модели.

Кроме того, методом наименьших квадратов Гаусса найти уравнение квадратичной регрессии .

Решение. 1). Найдем сначала точечные оценки выборок для переменных и . Выборочные средние значения и находим из соотношений

,

.

Для выборочных дисперсий и средних квадратичных уклонений получаем:

Отсюда

Для вычисления коэффициента линейной регрессии по формуле осталось найти смешанную сумму

Отсюда следует, что

Из формулы получаем оценку .

Таким образом, уравнение линейной регрессии имеет вид .

Теперь по формуле 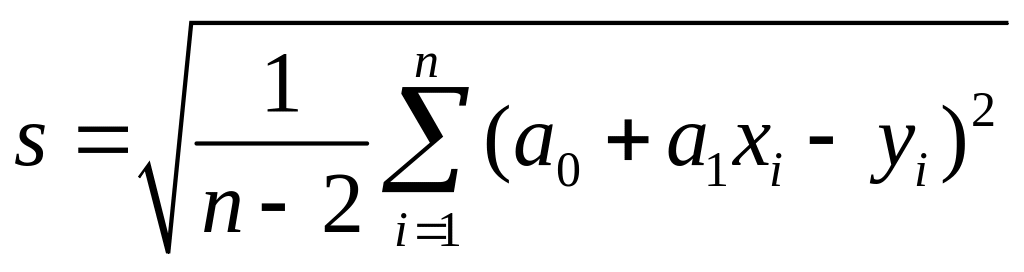мы можем найти точечную оценку параметра случайной величины :

Отсюда .

2) Найдем 95% доверительные интервалы для параметров и . Используем формулы

, .

При , , критические точки распределения Стьюдента и распределения можно найти по таблицам этих распределений, и они равны соответственно

,

Отсюда следует, что доверительный интервал для параметра уравнения регрессии есть

Аналогично, доверительный интервал для параметра имеет вид

3) Найдем среднюю добычу угля на одного рабочего для пласта мощностью м. Подставим в уравнение линейной регрессии :

4) Найдем 95% доверительные интервалы для средней и индивидуальной выработки рабочего для пласта мощностью м. Используем формулы:

, ,

для интервальной оценки средней выработки, и формулы

,

для интервальной оценки индивидуальной выработки. Получаем:

Аналогично, для интервальной оценки индивидуальной выработки получаем:

5) Проверим гипотезу о значимости уравнения регрессии на уровне значимости =0.05. Для этого найдем коэффициент детерминации по формуле

.

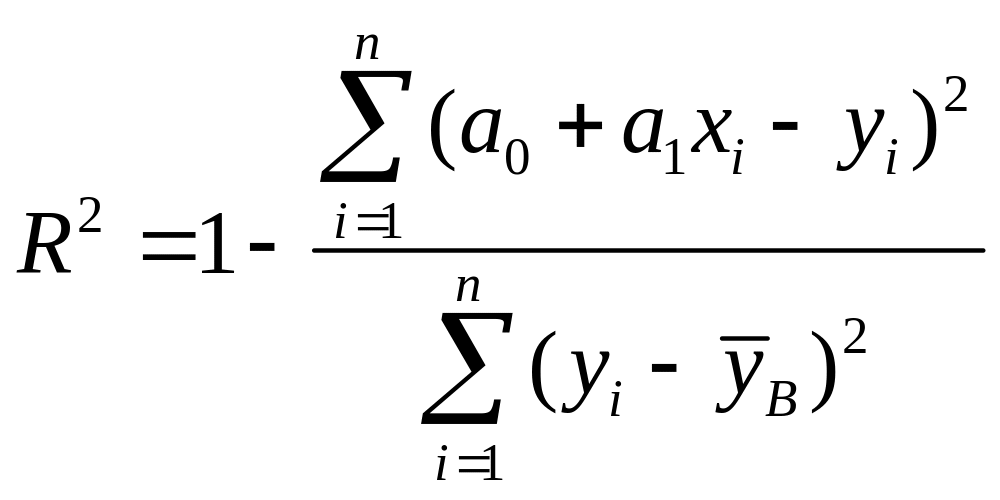Получаем: ,

Следовательно,

Критическая точка распределения ФишераСнедекора при уровне значимости =0.05 равна ,

откуда получаем, что, .

Следовательно, уравнение линейной регрессии следует признать незначимым на данном уровне значимости.

6) Коэффициент детерминации регрессионной модели был найден при проверке гипотезы о значимости уравнения регрессии. Поскольку , следует заключить, что в зависимости объясняемой переменной от наиболее существенную роль играют случайные факторы, а не линейная часть регрессии .

7) Найдем уравнение квадратичной регрессии . Для этого подсчитаем коэффициенты линейной системы уравнений, которая определяется из принципа наименьших квадратов Гаусса:

Часть коэффициентов этой системы фактически уже была найдена в предыдущих пунктах. А именно,

, ,

, ,

Осталось, следовательно, вычислить три коэффициента системы.

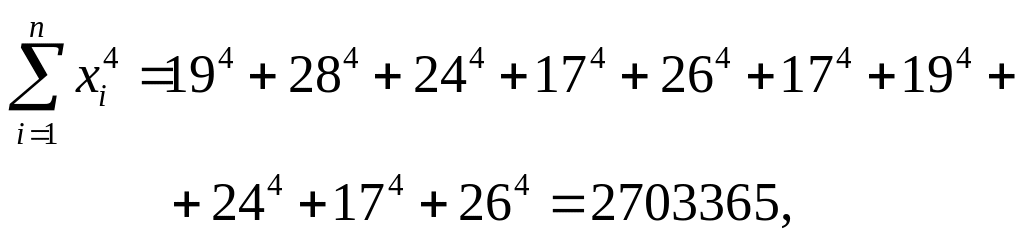
Получаем:

Для решения системы используем пакет символьных вычислений MATHCAD. Средствами этой программы решение системы линейных уравнений производится с помощью следующих командных строк.

Решениями системы являются числа

Таким образом, квадратичная регрессия имеет вид

В заключение, построим графики функций и на отрезке . Для построения графиков функций вновь используем программу MATHCAD.