Занятие №1 Тема: «Разработка структурной схемы сау по математической модели»

Цель: изучение объекта исследования - системы угловой стабилизации (СУС) упругого КА, разработка ее структурной схемы по математическому описанию, знакомство с пакетом Vissim и приобретение начальных навыков работы с ним.

Первоначальным этапом исследовании любой САУ с помощью Vissim является построение структурной схемы по ее математическому описанию. Объектом данного исследования является система угловой стабилизации космического аппарата.

Назначение и состав СУС

Система угловой стабилизации предназначена для долговременного поддержания заданной ориентации КА в пространстве. Процесс стабилизации можно считать удовлетворительным, если выполняются следующие условия:

- обеспечивается асимптотическая устойчивость нулевого значения вектора состояния объекта, включающего параметры ориентации и угловую скорость;

- при малых начальных отклонениях обеспечивать достаточно быструю сходимость вектора состояния к нулевому значению.

Минимальный состав СУС включает:

- объект управления КА, представимый как абсолютно жесткое центральное ядро с присоединенными к нему упругими элементами (панели солнечных батарей, антенны, штанги и др.) (рис.1);

- датчик угла, по информации которого определяется угловое отклонение аппарата от заданного положения и его угловая скорость;

- формирующее устройство, которое по информации о векторе состояния вырабатывает управляющий сигнал;

- исполнительные устройства (реактивные двигатели ориентации, инерционные маховики, гиродины).

Рис 1. Объект управления

Будем рассматривать задачу одноосной стабилизации относительно продольной оси аппарата Ох. В этом случае динамические уравнения КА имеют вид

(1)

(2)

Где - осевой момент инерции КА,

- коэффициенты взаимовлияния твердого ядра и упругих элементов,

- соответственно коэффициент демпфирования и частота первого тона колебаний.

Все указанные параметры задаются таблично (табл.1).

- переменные, соответствующие углу поворота КА относительно заданного положения и величине "смещения" упругого элемента относительно недеформированного состояния. Измеряются соответственно в радианах и метрах;

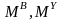- возмущающий и управляющий моменты, приложенные к аппарату.

Уравнение (1) отвечает вращению КА в пространстве, уравнение (2) -относительной динамике упругих элементов. Вместе они составляют описание объекта управления.

Приведенные уравнения наглядно отражают физическую природу рассматриваемого динамического процесса, поэтому в дальнейшем уравнения (1), (2) будем называть физической моделью. Действительно, левые части уравнений содержат соответственно угловое и линейное ускорения ядра и элемента, а правые части - моменты и силы;

- момент, действующий на ядро со стороны упругого элемента;

- сила, действующая на упругий элемент со стороны ядра.

Слагаемые 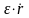и в уравнении (2) обусловлены упругими свойствами элемента и определяют колебательный характер динамического процесса.

Для исследования путем численного моделирования физическая модель в таком виде не пригодна. Действительно, из уравнения (1) мы можем определить значение переменной в момент времени , т.е.

а - из второго уравнения

что невозможно, поскольку в данный момент еще не определено. Этого можно избежать искусственным введением во второе уравнение запаздывания, вместо использовав . Такой способ не совсем корректен, поскольку полученная при этом дискретная модель процесса структурно не адекватна порождаемой непрерывной модели (в непрерывную модель как бы добавляется звено запаздывания). В ряде случаев такой переход не ведет к существенному искажению динамики процесса и является допустимым. Однако для рассматриваемой системы наличие запаздывания в контуре управления может привести не только к ухудшению качества системы, но даже к потере устойчивости, в чем мы убедимся в одной из лабораторных работ. Поэтому мы поступим иначе. Путем эквивалентных математических преобразований приведем уравнения (1), (2) к другому виду. Рассматривая их как систему, после исключения из первого уравнения слагаемого, содержащего 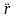, получим

(3)

Уравнение (3) совместно с уравнением (2) и составляют преобразованную математическую модель вращения упругого КА.

Из уравнения (3) передаточная функция от к равна . Из уравнения (2) получим передаточную функцию от к .

Такой системе соответствует следующая структурная схема:

Рис.2. Структурная схема объекта управления

Перейдем к формированию управления. На борту управляющий сигнал вычисляется бортовым вычислителем. По алгоритму, разработанному еще на Земле, с учетом информации, поступающей с датчиков, вычисляется величина управляющего момента, требуемая в данный момент для угловой стабилизации аппарата.

Управление построим по принципу обратной связи.

Управляющий момент будем формировать в соответствии с законом:

в котором - величина запаздывания, обусловленная временем прохождения информационною сигнала в контуре управления (будем пригашать ее равной 0.1 сек.); - так называемые коэффициент регулятора, являющиеся настраиваемыми параметрами СУС. Их выбирают такими, чтобы САУ была устойчивой и ее функционирование отвечало требуемым оценкам качества.

Такой принцип формирования управления называется линейным ПД -регулятором (в закон управления входят пропорциональная и дифференциальная составляющие переменной ) .

Будем считать, что датчики информации обеспечивают абсолютно точное измерение текущих значений переменных и . В этом случае СУС можно представить в виде следующей замкнутой схемы:

Рис.3. Структурная схема СУС с ПД-ретулятором

На этом разработку структурной схемы можно считать законченной.

ЗАДАНИЕ:

1. Входящие в схему элементы сопоставить с типовыми блоками Vissim.

2. Для исходных данных своего варианта (см. таблицу в приложении) вычислить коэффициенты типовых блоков Vissim, из которых будет набрана структурная схема.

3. Набрать структурную схему. Для проверки работоспособности и адекватности модели в блоках-интегратор задавать не нулевые начальные условия.

4. Полученную схему и результаты вывести в отчет.

КОНТРОЛЬНЫЕ ВОПРОСЫ:

1. Назначение и состав СУС КА. Каков физический смысл входящих в математическую модель элементов.

2. Что такое регулятор, ПД-регулятор?

3. Из каких блоков состоит структурная схема СУС КА.

4. Основные этапы моделирования.