Глава 3. Сложные химические реакции. Формальная кинетика.

Параллельные реакции.

Простейшая параллельная реакция изображается схемой . Предполагаем, что температура постоянна. Пронумеровав стадии, можно записать

	K1
1. А	→	В
	K2
2. А	→	С

Обе стадии протекают одновременно, К₁ и К₂ пропорциональны вероятностям протекания процессов.

В момент времени t=0: [A]₀=a₀, [B]₀=b₀, [C]₀=c₀. Для произвольного момента времени введем вспомогательную величину х – количество исходного вещества А, прореагировавшего к моменту времени t. Для произвольного момента времени t: [A]=a₀-x, [B], [C]. Попытаемся записать кинетическое уравнение для исходного компонента А.

В общем случае для реакции ее скорость определяется согласно .

В нашем случае .

Результат: ,

.

Определим теперь [B] и [C].

Пусть b_o=c_o=0. Тогда при К₁>K₂

Для b_o=c_o=0 , , .

при . (1)

, где δ и К₁ являются параметрами. (2)

Следовательно, используя соотношения (1) и (2) и экспериментально определяя пару концентраций, можно определить К₁ и К₂.

Дома: Рассмотреть двухстадийную параллельную реакцию

	K1
(1) А		В
	K1’
	K2
(2) А		С
	K2’

При заданных константах и постоянной температуре получить решение этой задачи, т.е. [A], [B], [C], если b_o=c_o=0.

Для задачи можно ввести суммарную скорость реакции и скорости реакций отдельных стадий.

	K1
1. А	→	В
	K2
2. А	→	С

Продифференцируем ранее полученные выражения для концентраций. Суммарная скорость реакции по исходному компоненту:

.

Скорости стадий: , .

Общий признак для всех параллельных реакций: w=w₁+w₂, т.е. для параллельных реакций суммарная скорость реакции равна сумме скоростей отдельных стадий.

Если реакция более общая, то для n-стадийной реакции .

Пример. СН₄+О₂→СО₂+Н₂О – суммарное уравнение реакции.

Отдельных стадий 350.

Из полученного закона следует, что в случае, когда какая-либо стадия протекает много быстрее других стадий, то скорость реакции определяется в основном скоростью наиболее быстрой стадии.

Дома: рассмотреть параллельную реакцию, состоящую из двух бимолекулярных стадий:

	K1
1. А + В	→	C + D
	K2
2. А + B	→	С’ + D’

Предполагаем, что температура постоянна; начальные условия (t=0): [A]_o=a_o, [B]_o=b_o, [C]_o=[D]_o=[C’]_o=[D’]_o=0. Найти решение для концентраций. После получения общих результатов рассмотреть случай, когда a_o=b_o.

Способ решения: для произвольного момента времени t вводим переменную х – количество прореагировавшего вещества А к моменту времени t. Тогда текущая концентрация [A]=a_o-x; т.к. на одну исчезнувшую молекулу А исчезает одна молекула В, то [B]=b_o-x.

После получения общих результатов предложить экспериментальные способы получения К₁ и К₂.

Дома: рассмотреть реакцию

	K1
1. А	→	В
	K2
2. 2А	→	С

Температура постоянна.

Запишем для данной реакции систему уравнений:

(1) (т.к. )

(2)

(3)

Уравнения (1), (2), (3) полностью описывают схему.

Начальные условия (t=0): [A]_o=a_o, [B]_o=b_o, [C]_o=c_o.

Способ решения: для произвольного момента времени t вводим переменную х – количество прореагировавшего вещества А к моменту времени t. Тогда текущая концентрация [A]=a_o-x. Необходимо довести задачу до решения по концентрациям. После получения общих результатов предложить экспериментальные способы получения К₁ и К₂.

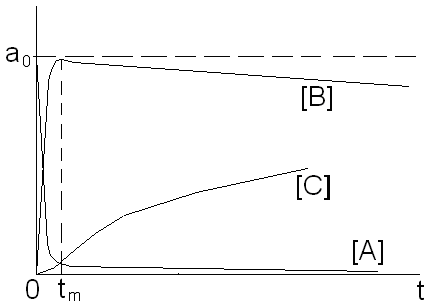
Последовательные реакции.

Простейшая последовательная реакция 1-го порядка:

	K1		K2
А	→	В	→	С

Определим при постоянной температуре зависимость всех концентраций от времени. Начальные условия (t=0): [A]_o=a_o, [B]_o=b_o, [C]_o=c_o.

Для произвольного момента времени t вводим переменную х – количество прореагировавшего вещества А к моменту времени t. Тогда текущая концентрация [A]=a_o-x.

Нужно ввести еще одну переменную y – количество получившегося конечного продукта к моменту времени t. Тогда [C]=c_o+y, [B]=b_o+x-y (В образуется из вещества А и одновременно расходуется на образование С).

В начальный момент времени (t=0): х_о=у_о=0.

Если b_o=c_o=0, то [A]=a_o-x, [B]=x-y, [C]=y.

Система кинетических уравнений для этой реакции:

Результат: , .

Отсюда

Результат: .

.

Если величины К₁ и К₂ близки, то

Максимум на зависимости [B](t) и S-образная форма графика для [C] (конечного продукта реакции) являются характерными особенностями последовательных реакций.

Определим t_m и [B]_m: , следовательно, ,

Дома: проанализировать полученные решения для предельного случая К₁=К₂ (либо снова решить задачу при К₁=К₂, либо взять пределы всех выражений при К₁→К₂, либо представить К₂ как К₂=К₁+ΔК, ΔК<< К₁, К₁=К и разложить в ряд Тейлора, ограничившись первыми членами.

Результаты: , , , , .

Рассмотрим случай, когда К₁>>К₂ (первая стадия протекает гораздо быстрее второй).

, , - мало,

,

.

Из графика следует, что начальный период очень сжат и им можно пренебречь; процесс определяется второй стадией (медленной).

Общий вывод: для любой последовательной реакции характерной чертой является то, что суммарная скорость процесса определяется скоростью наиболее медленной стадии.

Рассмотрим случай, когда К₂>>К₁ (вторая стадия протекает гораздо быстрее первой).

, - мало, - мало,

- устанавливается квазистационарное равновесие между исходным (А) и промежуточным (В) компонентом.

.

В данном случае первая стадия – наиболее медленная; она и определяет скорость процесса.

_{Пусть теперь bo и co} .

	K1		K2
А	→	В	→	С
	w1		w2

Результат: ; , .

Дома: для случая b_o и c_o определить t_m и [B]_m и дать анализ этого случая.

Дома: исследовать формальную кинетику трехстадийной химической реакции

	K1		K2		K3
А	→	В	→	С	→	D

Начальные условия (t=0): [A]_o=a_o, b_o=c_o=d_o=0.

Явление катализа. Каталитические химические реакции.

Основные определения и понятия.

Определение. Катализом называется возбуждение химической реакции или изменение ее скорости в присутствии некоторых веществ, называемых катализаторами.

Положительный катализ – скорость химической реакции возрастает; отрицательный катализ – скорость химической реакции уменьшается.

Катализатором называется вещество, ускоряющее реакцию, но до и после реакции остающееся в неизменном количестве и с неизменными химическими и физическими свойствами.

Отрицательные катализаторы называются ингибиторами.

Химическую реакцию с участием катализатора можно записать в форме

	K
А + В + Х	→	АВ+Х

Здесь А и В – исходные вещества, АВ – продукт реакции.

Некаталитическая реакция:

	Kо
А + В	→	АВ.

Если Х ускоряет реакцию, то K>K_o или K>>K_o.

Если реакция обратимая

	K
А + В + Х		АВ+Х
	K’
	Kо
А + В		АВ,
	Ko’

то для некатализированной реакции , для каталитической реакции . Вывод: любое воздействие катализатора не смещает равновесие ни в какую сторону, но скорость достижения равновесия изменяется.

Катализатор обладает ярко выраженной специфичностью действия: на ряд химически однотипных реакций катализатор оказывает различное воздействие; если исходная система может реагировать по разным направлениям, то катализатор на различные направления оказывает различное влияние; катализатор может менять направление химической реакции; если известно, что некоторые наборы веществ являются катализаторами и оказывают различное действие на некоторую реакцию, то смешанный катализатор обладает большей активностью, чем просто сумма активностей отдельных катализаторов; катализаторы очень чувствительны к наличию определенных веществ в реагирующей системе.

Определение. Вещества, увеличивающие активность катализаторов, называются промоторами, а вещества, уменьшающие активность катализаторов, называются каталитическими ядами.

Две группы явлений катализа: гомогенный и гетерогенный катализ.

Определение. Гомогенным называется катализ, когда катализатор и реагирующие компоненты находятся в одной фазе. Гетерогенным называется катализ, когда катализатор образует обособленную фазу по отношению к реагирующим веществам.

Определение. Гомогенной называется система, внутри которой нет поверхностей раздела, отделяющих друг от друга части системы, которые различаются по своим физическим и химическим свойствам. Гетерогенной называется система, в которой такие поверхности имеются.

От понятий гомогенных и гетерогенных систем нужно отличать понятия систем однородных и неоднородных.

Определение. Однородной называется система, в которой все участки объема обладают одинаковым составом (химически однородная система) или одинаковыми физическими свойствами (физически однородная система). В противном случае система называется неоднородной.

Неоднородная система может быть и гомогенной, если ее состав и свойства изменяются непрерывно от одного участка к другому и не образуются поверхности раздела.

Определение. Фазой называется совокупность всех гомогенных частей системы, одинаковых по составу и по всем физическим и химическим свойствам и ограниченная от других частей системы некоторой поверхностью раздела.

Пример. Гомогенный катализ:

2СО + О₂ → 2СО₂ – взрывная цепная реакция.

При добавлении в исходную смесь водорода или паров воды реакция пойдет при температуре менее 250 ^оС.

Катализаторы этой реакции – все водородосодержащие соединения.

Гетерогенный катализ:

Н₂ → 2Н

Заметно эта реакция идет обычным образом при температуре более 2000 К (термическое разложение). В присутствии соединений платины реакция идет уже при комнатной температуре.

Определение. Микрогетерогенный катализ (промежуточная форма между гомогенным и гетерогенным катализом) – катализатор образует обособленную фазу, но находится в мелкодисперсном состоянии (частицы с размерами ~10^-5 см). Вещество катализатора находится в коллоидном состоянии, что обусловливает его высокую активность. Важнейший случай – биологический ферментативный катализ.

Определение. Если реакция катализируется одним из своих собственных продуктов, такая реакция называется автокаталитической.

Гомогенный катализ.

Простейшее объяснение: катализатор вступает с катализируемыми веществами в некоторые промежуточные процессы, но по завершении реакции катализатор должен выйти из системы и вернуться к первоначальному состоянию (в неизменном количестве, с неизменными химическими и физическими свойствами).

Некаталитическая реакция:

	Kо
0. АВ	→	А + В, T=const, скорость реакции wo.

Каталитический процесс:

1. АВ + Х	→	АВХ – промежуточное неустойчивое вещество с высокой реакционной способностью
2. AВХ	→	А + В+Х

Процессы 1 и 2 характеризуются скоростью w. , .

Промежуточное вещество из-за высокой реакционной способности не может накапливаться в значительных количествах.

Задачи: 1. Выяснение механизма реакции;

2. Выяснение, почему катализатор воздействует именно на эту реакцию;

3. Если катализатор увеличивает скорость, то почему скорость увеличивается?

~К~ , T=const, следовательно, увеличить скорость реакции можно только уменьшив энергию активации. Какова причина снижения энергии активации?

Формальная кинетика каталитических реакций.

	Kо
0. АВ	→	А + В, T=const, скорость реакции wo.

	K1
1. АВ + Х	→ K2	АВХ		типично последовательная реакция, w, возможный вариант 1
2. AВХ	→	А + В+Х

	K1		K2
(АВ + Х	→	AВX	→	A + B + X)

Каков механизм реакции?

Можно придумать несколько логически обоснованных схем, которые анализируются по вероятности (наименее вероятные отбрасываются).

	K1’
1. АВ + Х	→ K2’	АХ + B		возможный вариант 2
2. AХ	→	А + Х

	K1’’
1. АВ + Х	→ K2’’	А + BX		возможный вариант 3
2. BХ	→	B + Х

Пусть анализ показывает, что наиболее вероятная схема – вариант 1. Пусть заданы начальные условия (t=0): [AB]_o=a_o.

Запишем полную систему кинетических уравнений.

Предполагаем, что начальный период инициирования реакции прошел, и все имеющиеся стадии протекают параллельно.

Для каждой стадии справедлив закон действующих масс. Т.к. рассматриваем параллельный процесс, то суммарная скорость равна сумме скоростей отдельных стадий.

Полагаем, что , и реакцию 0 не рассматриваем.

(1) , отсюда

(2)

(3)

(4)

(5)

Дополнительное алгебраическое уравнение (5) отражает сохранение катализатора в процессе реакции:

- закон сохранения вещества катализатора.

Отсюда (уравнение (5)).

Суммарную скорость сложной реакции можно определить через концентрации конечных стабильных продуктов реакции:

Утверждение (см. также раздел «Последовательные реакции»): промежуточные компоненты с высокой реакционной способностью быстро образуются и быстро расходуются.

Принцип Боденштейна: в определенных условиях может возникнуть ситуация, когда суммарные скорости образования всех или части промежуточных веществ сравняются с суммарными скоростями их расходования (возникает т.н. состояние квазистационарного равновесия). В этом случае временные производные концентраций всех промежуточных компонентов равны 0.

Тогда (3) ,

Из этого равенства и закона сохранения вещества катализатора получаем, что

,

,

- такой вид имеет скорость реакции 1-го порядка.

.

Проведем анализ.

1. Предположим, что ([AB] мала).

Тогда - нет зависимости от [AB]. .

2. Предположим, что .

Тогда , - нулевой порядок реакции.

Свойство гомогенной каталитической реакции менять порядок в ходе реакции – характерное свойство этой реакции.

Дома: рассмотреть эту же задачу, определив скорость реакции не по конечным продуктам, а по исходным компонентам: и показать, что конечный результат будет тот же.

Рассмотрим теперь отношение скорости катализированной реакции к скорости некатализированной реакции: (или >>1).

Рассмотрим 2 предельных случая:

1. .

(т.к. энергия активации Е₁<E_o.

2. .

Все зависит от снижения эффективной энергии активации.

Гетерогенный катализ. Основные понятия.

Ускорение реакции при гетерогенном катализе также вызывается изменением пути реакции, и в большинстве случаев связано со снижением энергии активации в присутствии катализатора. Изменение пути реакции осуществляется из-за образования промежуточных веществ как и при гомогенном катализе, но путь более сложен, 3 стадии:

1. Диффузия реагирующих компонентов к поверхности катализатора.

2. Адсорбция (абсорбция) реагентов на поверхности катализатора и химическая реакция на поверхности катализатора.

3. Диффузия продуктов реакции обратно в объем.

В большинстве случаев стадии 1 и 3 протекают много быстрее, чем стадия 2. Т.к. все стадии представляют собой последовательный процесс (1) → (2) → (3), то скорость гетерогенного катализа в основном определяется скоростью стадии 2.

Определение. Адсорбция – физико-химический процесс взаимодействия молекул газа с активными точками поверхности катализатора, в результате чего молекулы «прилипают» к активным точкам и удерживаются в течение времени, называемом временем жизни молекул газа в адсорбированном состоянии: t_ж = f (T,p).

Чисто физическое удерживание:

Поверхность катализатора:

	Kо
А + В	→	АВ (некатализированная реакция)
	K
А + В + Х	→	АВ + Х (катализированная реакция)

Молекула А «прилипает» к поверхности катализатора в т.н. активной точке. «Прилипнув», молекула А деформируется и переходит в активное состояние. Если в эту же область подходит молекула А, возможен процесс А* + В → АВ* - такой процесс более вероятен, чем реакция между неактивными компонентами, скорость его выше, процесс идет быстрее).Затем происходит десорбция – отрыв образовавшейся молекулы АВ (или молекулы А, если химическое взаимодействие не имело места).

Чисто химическое удерживание:

Молекула А образует поверхностное соединение с катализатором:

А + К → (АК)_поверх

(АК)_поверх + В → АВ + К

Если молекулы удерживаются на поверхности – адсорбция, если при взаимодействии с поверхностью катализатора молекула проникает внутрь объема катализатора и там образует поверхностное соединение – абсорбция.

Толщина мономолекулярного слоя ~d_o – размер молекулы (т.н. Ван-дер-ваальсовский слой). В щели напряженность Ван-дер-ваальсовского поля в 2 раза выше, чем на поверхности, т.к. накладываются поля от стенок щели. В силу этого вероятность обнаружить активную точку в щелях и различных дефектах на поверхности катализатора выше, чем на гладкой поверхности.

Методами теории размерности приближенно решим задачу о гетерогенном катализе.

Введем понятие среднего числа активных точек на единице поверхности катализатора.

Введем величину , которая определяет долю «заполненных» активных точек (точки, на которых поглотились молекулы). Тогда (1-) – доля свободных (незаполненных) активных точек.

Давление Р пропорционально концентрации реагирующих компонентов.

Введем также характерные скорости для всех трех стадий:

Скорость адсорбции ; скорость десорбции ; скорость химической реакции .

Скорость диффузии не определяет процесс, т.к. стадии 1 и 3 протекают много быстрее стадии 2.

Решаем задачу в установившемся квазистационарном приближении: ; тогда . Из этого равенства находим : в квазистационарном случае . Тогда квазистационарная скорость .

Предельные случаи: 1. : ; 2. : .

Изменение порядка химической реакции в зависимости от изменения условий (давление, Р) – характерное свойство гетерогенного катализа.

На рис. Т₁<T₂<T₃. Чем больше температура в системе, тем меньше время жизни адсорбированного состояния – все процессы активизируются, их скорости увеличиваются. , , .

Автокатализ.

Рассмотрим процесс А → В, причем В катализирует реакцию. Нарастание концентрации В все более увеличивает скорость химической реакции (предполагаем, что катализ положителен).

Характерные черты автокатализа:

График, характерный для любой автокаталитической реакции:

Наблюдаемые стадии:

	Kо
0. А	→	В, wo - скорость некатализированной реакции (нет заметного влияния В на реакцию).

t_и – время перехода к высокоскоростному процессу, период t_и называется периодом индукции.

I – стадия резкого нарастания скорости реакции.

w_max>>w_o. Конечность w_max связана с тем, что концентрация В не может возрастать до бесконечности, скорость реакции начинает уменьшаться по мере расходования А.

II – стадия падения скорости реакции.

Снижение скорости реакции на этой стадии обусловлено малыми концентрациями А. .

t_и не является физической константой, т.к. ее значение во многом зависит от чувствительности метода исследования реакции.

Примеры автокаталитических реакций:

1) NiO + H₂ → H₂O + Ni

2) CuO + H₂ → H₂O + Cu

Практически все реакции окислов металлов с водородом идут до полного восстановления свободного металла. Свободный металл воздействует на начальные компоненты – автокатализ.

Рассмотрим реакцию А → В (В – катализатор процесса).

Рассмотрим процесс в общих чертах. Эта реакция – автокаталитическая реакция 1-го порядка. Механизм автокатализа чрезвычайно сложен. Пусть А → В – суммарное уравнение. Реальный процесс протекает в несколько последовательных стадий. Среди этих стадий обязательно найдется хотя бы 1 процесс взаимодействия вещества А с веществом В – катализатором (обозначим этот процесс (i)). Исследования показали, что эта стадия является, как правило, наиболее медленной.

Т.к. все стадии последовательные, то скорость реакции зависит от скорости стадии (i); вместо процесса А → В появляется процесс продукты реакции.

Рассмотрим эту реакцию. Начальные условия (t=0): [A]_o=a_o, [B]_o=b_o. Введем х – количество прореагировавшего к моменту времени t компонента А.

[A]=a_o-x.

(*)

равенство приближенное, т.к. отбросили другие стадии, где участвует вещество А.

; отсюда .

При t=0: если b_o=0, то х=0, , следовательно, w_o=0 (!?) – такое противоречие получилось, т.к. использовали приближенное равенство (*).

Метод, предложенный Освальдом (автокаталитическая и некаталитическая реакции протекают одновременно):

(**)

Тогда .

Противоречие снимается: .

Приведем уравнение (**) к форме уравнения (*): выполним тождественные преобразования: a_o=a, b_o+K_o/K=b.

Тогда (***)

;

, следовательно, .

Подставляя значение x_m в выражение для dx/dt, получаем .

Из условия dx/dt=0 определяем .

Уравнение (***) – приближенное. Реальные уравнения автокатализа отличаются от (***), например (****), где n и m – константы, определяемые опытным путем.

Реакциями автокатализа являются цепные разветвленные реакции.

Дома: ввести переменную и преобразовать уравнение (****) в форму для случаев, когда а) m,n=1; б) m,n 1.

Сопряженные реакции.

Определение. Сопряженная реакция – система двух реакций, происходящих в одной и той же среде, из которых одна зависит в своем развитии от другой.

	K1
(1) А + В	→	продукты реакции
	K2
(2) А + С	→	продукты реакции

Если одна из этих реакций, например, А+В, идет независимо от другой, то реакция А+С может идти только при условии (наличии) развивающейся 1-й реакции.

Явление, когда одна из реакций зависит от хода другой, называется явлением химической индукции.

Независимая реакция (1) называется первичной реакцией, реакция (2) – зависимая – называется вторичной реакцией. Первичная реакция называется также индуцирующей, а вторичная – индуцируемой. Участвующее в обеих реакциях вещество А называется актором, В – индуктором, С – акцептором (принимает на себя влияние первичной реакции).

Явление сопряжения называется положительным, если первичная реакция ускоряет вторичную, и отрицательным в противном случае.

Взаимным сопряжением называется случай, когда обе реакции влияют друг на друга, причем это влияние может быть как положительным, так и отрицательным.

Явление автокатализа можно рассматривать как самосопряженную реакцию.

Степень влияния первичной реакции на вторичную определяется величиной I, называемой фактором индукции.

, где - доля актора, участвующая во вторичной реакции, - доля актора, участвующая в первичной реакции.

Примеры.

1) H₂ + Cl₂ → 2HCl

Если водород и хлор взяты чистыми, то эта реакция до 250 ^оС не идет. При наличии примесей, например, паров натрия, эта реакция быстро возбуждается и приобретает взрывной характер.

2Na + Cl₂ → 2NaCl – первичная реакция (1)

H₂ + Cl₂ → 2HCl (2)

~10⁴ – 10⁵ (опыт показывает, что влияние реакции (1) на реакцию (2) велико. Приведенное значение I означает, что на 1 молекулу NaCl образуется 10⁴ – 10⁵ молекул HCl.

Объяснение:

Когда реакция H₂ + Cl₂ → 2HCl уже возбуждена, реализуются следующие процессы:

0. Cl₂ + M → 2Cl + M

1. Cl + H₂ → HCl + H

2. H + Cl₂ → HCl + Cl

Роль натрия: Na + Cl₂ → NaCl + Cl – эта реакция является значительно более эффективным поставщиком атомов Cl, чем процесс 0. Образующийся свободный атом хлора возбуждает процесс 1., реализуя сопряжение реакций.

2. 2СО + О₂ → 2СО₂

В чистых веществах эта реакция в большом интервале температур не идет; при ее возбуждении реакция протекает по механизму цепной разветвленной реакции.

Если в систему добавить молекулярный водород, то реакция быстро возбуждается и приобретает характер взрыва.

2Н₂ + О₂ → 2Н₂О (1)

2СО + О₂ → 2СО₂ (2)

~10⁴ – 10⁵.

Подробно распишем основные элементарные процессы, протекающие для реакции (1):

0. Н₂ + О₂ → 2ОН

1. ОН + Н₂ → Н₂О + Н

2. Н + О₂ → ОН + О

3. О + Н₂ → ОН + Н

Переносчиками влияния реакции (1) на реакцию (2) является не Н₂, а продукты его реакций О и ОН, которые и являются реальными индукторами:

СО + ОН →СО₂ + Н

СО + О → СО₂* → СО₂ + h

Большое значение I говорит о том, что вторичная реакция является цепной. Если рассматривать вторичные реакции нецепного характера, то I будет порядка 1.

Общий вывод: Эксперимент показывает, что реальным переносчиком влияния реакции (1) на реакцию (2) является не сам индуктор как таковой, а некоторые промежуточные вещества, образующиеся в ходе реакции (1).

Реальную реакцию сопряжения можно записать следующим образом:

	K1
(1) А + В	→	Х + Р* (прочие продукты реакции)
	K2
(2) Х + С	→	Р

Здесь Х – реальный источник влияния реакции (1) на реакцию (2).

Такая запись эквивалентна записи

	K1
(1) А + В	→	продукты реакции
	K2
(2) А + С	→	продукты реакции

При постоянной температуре система кинетических уравнений имеет вид

(1,2)

(3)

(4)

(5)

Начальные условия (t=0): если [A]_o=[B]_o=[C]_o=a_o, если К₁=К₂, то эту задачу можно решить в аналитической форме:

Особенность сопряженных реакций: один из исходных компонентов ([C]) в начальный момент времени (t*) меняется слабо (на графике зависимости [C](t) есть «площадка»).

Для простейшей последовательной реакции минимальное количество компонентов – 1, а для сопряженной – 3.

Согласно известным результатам исследований, в большинстве сопряженных реакций К₁>>К₂.

Нами был рассмотрен случай, когда концентрация вещества В уменьшается со временем. Однако могут быть и другие типы сопряжений, например:

	K1
(1) А + В	→	продукты реакции
	K2
(2) А + С	→	продукты реакции + В

Здесь индуктор В играет еще и роль катализатора. Такие реакции похожи на реакции катализа.

	K1
(1) А + В	→	продукты реакции
	K2
(2) А + С	→	продукты реакции + 2В

Здесь концентрация индуктора со временем возрастает. Эти реакции эквивалентны реакциям автокатализа.

Теория мономолекулярных реакций.

	K
А	→	продукты реакции

Эксперимент показывает, что эти реакции на самом деле не являются простыми, их механизм сложен и зачастую очень сложен.

	K1		K2
А	→	А*	→	продукты реакции

Образование и расходование промежуточного вещества А* - самое неясное место в реакции.

Нами будут рассматриваться только тепловые реакции. Для мономолекулярных тепловых реакций известно: скорость мономолекулярной реакции сильно зависит от температуры и эта зависимость подчиняется закону Аррениуса – отсюда следует, что реакция имеет черты бимолекулярной реакции. Эффективная константа скорости сложным образом меняется во времени, можно выделить либо 1-й, либо 2-й порядок реакции.

Активные промежуточные частицы (активные центры) образуются за счет бимолекулярных столкновений, поэтому бимолекулярные процессы играют в мономолекулярных процессах значительную роль.

Рассмотрим приведенную выше схему превращения вещества А через образование промежуточного вещества А*. Если первая стадия процесса протекает много медленнее второй, то активные частицы появляются с трудом, а расходуются быстро. Таким образом, наиболее медленной является стадия образования активных центров, которая представляет собой бимолекулярный процесс. Вследствие этого наблюдается эффективный второй порядок реакции.

Если вторая стадия протекает много медленнее первой, то получим первый порядок реакции.

Изменением внешних условий можно менять порядок реакции: например, при больших давлениях наблюдается первый порядок, при малых – второй порядок.

Схема Линдемана:

	Kа
(1) А + А	→	А* + А (процесс активации)
	Kр
(2) А*	→	продукты реакции (Р) (процесс распада; как индикатор выделим один из продуктов (Р))
	Kд
(3) А* + А	→	А+ А (процесс дезактивации)

Эта схема – простейшая, не отражает всех микромолекулярных процессов.

Запишем систему кинетических уравнений:

1)

2)

3) - этим уравнением определяется скорость процесса.

Для определения скорости нужно найти [A*]=f(t).

Начальные условия (t=0): [A]_o=a_o, [P]_o=p_o,…

Предположим, что условия протекания реакции таковы, что она действительно протекает квазистационарно. Условия протекания реакции: давление и температура постоянны.

Обозначим [A*]=n*, [A]=n.

Тогда 2) в силу квазистационарности.

3)

Из 2) определяем ;

.

Здесь (обозначили ).

Тогда - получили линеаризованную зависимость.

Обычно К_аК_д, тогда .

Рассмотрим полученное выражение для К: .

Предельные случаи: 1) (n – мало). Тогда , - второй порядок реакции.

2) (n – велико). Тогда , - первый порядок реакции.

Т.к. n~Р – давлению среды, то процесс носит истинный мономолекулярный характер при высоких давлениях, а бимолекулярный процесс имеет место при низких давлениях:

К_а ~10^-10 см³·молек^-1·сек^-1

К_р ~10¹³ сек^-1

К_д ~ 10^-10 см³·молек^-1·сек^-1

Для Р=1 атм n ~ 10¹⁹ молек/см³.

Тогда критическое давление перехода к 1-му порядку реакции составит Р_кр10000 атм – при таком давлении будет наблюдаться неравенство . Поэтому истинный первый порядок в эксперименте может и не проявиться по чисто техническим причинам.

Примечание: т.к. при наличии квазистационарного режима , а , то - разности скоростей процессов активации и дезактивации.

Дома: при наличии в схеме Линдемана обратных реакций составить полную систему кинетических уравнений.

Тримолекулярные реакции. Основные понятия, механизм и кинетика.

Примеры:

О + О + М → О₂ + М (В общем виде: R₁^• + R₂^• + M → R₁R₂ + M)

Н + Н + М → Н₂ + М

Cl + Cl + M → Cl₂ + M

H + Cl + M → HCl + M

Здесь М – любая третья частица.

Рассмотрим подробнее реакцию О + О + М → О₂ + М. Эта реакция идет даже при комнатной температуре (значит, энергия активации для нее близка к 0).

Экспериментальные данные:

М	КIII, см6·молек-2·сек-1	Примечание
Ar Kr Xe	0,74·10-33 1,48·10-33 0,44·10-32	Константа скорости почти совпадает с числом тройных соударений
O O2	0,39·10-29 1,30·10-29	Аномалия: константа скорости превышает число тройных соударений – вывод: тримолекулярная реакция идет по сложному механизму.

Наиболее вероятные процессы этой реакции:

	K1
(1) О + О	→	О2*
	K2
(2) О2*	→	О + О
	K3
(3) О2* + М	→	О2* + М

Здесь [М=О, О₂, О₂*].

Таким образом, схема реакции имеет вид последовательно-параллельной реакции:

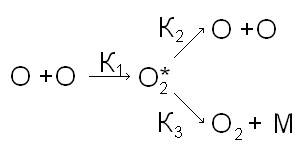
В зависимости от величин констант, преобладают либо свойства последовательной реакции, либо свойства параллельной реакции.

Предполагая, что реакция протекает квазистационарно, запишем систему кинетически уравнений:

1) ;

2) ;

Отсюда ;

.

Предельные случаи:

1) K₂>>K₃[M]: ; - порядок реакции – третий;

2) K₃[M]>> ) K₂: ; - порядок реакции – второй.

Большие давления, при которых реализуется 2-й порядок, могут быть недостижимы.

Рассмотрим случай малых давлений, когда .

Т.к. , , , то .

Обозначим Е₁+Е₂-Е₃=Е_эфф; при определенном соотношении между энергиями активации реакций 1, 2 и 3 Е_эфф может быть меньше 0.