Глава 2. Теория элементарного химического акта.

1) Постановка задачи.

Определение. Элементарным химическим актом (элементарным химическим процессом) называется химический процесс, протекающий в одну стадию.

H₂ + Cl₂ → 2HCl

Стадии:

0) стадия инициирования: при нагреве сначала распадается Cl₂, а потом H₂, если температуры не слишком высокие)

	Kо
Cl2 + М	→	2 Cl + М
	K1
1) Cl + H2	→	НCl + Н
	K2
2) Н + Cl2	→	НCl + Cl
	K3
3) Н + Н + М	→	Н2 + М
	K4
4) Н + Cl + М	→	НCl + М
	K5
5) Cl + Cl + М	→	Cl2 + М

В этой системе процессы 1) и 2) – процессы продолжения цепи, процессы 3), 4), 5) – процессы гибели активных центров.

В системе есть частицы: начальные (H₂ и Cl₂), конечные (HCl), промежуточные (H, Cl).

Если из целой системы выделяем подсистему, то реакция, протекающая в этой подсистеме, называется элементарной стадией (элементарная стадия состоит из множества однотипных реакций). Если «пронумеровать» все молекулы, то будем получать вероятность процесса конкретного взаимодействия w_i, если перебрать все «номера», получим набор вероятностей конкретных взаимодействий. Считаем, что общие характеристики (давление, температура) заданы. Разные вероятности получаются из-за различного состояния различных частиц.

Квантовая механика позволяет найти среднюю вероятность, которая определяет константу скорости реакции.

Опыт показывает, что частицы вещества обладают и корпускулярными, и волновыми свойствами (квантовомеханический корпускулярно-волновой дуализм). Волновые свойства отдельной микрочастицы описываются т.н. волновой функцией Ψ (x,y,z,t) (в общем случае это комплексная функция). Физический смысл Ψ: ׀Ψ(x,y,z,t)׀dxdydz – вероятность того, что в некоторый момент времени t частица находится в элементарном объеме dxdydz. Для определения волновой функции отдельно взятой микрочастицы, движущейся в потенциальном поле, служит уравнение Шредингера

iħ (*)

ħ= ,

Из-за линейности (*) решение определяется с точностью до постоянного множителя.

(2π),

Уравнение (*) (т.н. волновое уравнение Шредингера) – общий случай, который описывает взаимодействия (переходы атомов или молекул из одного состояния в другое, взаимодействие между частицами). Поэтому уравнение (*) получило название временного волнового уравнения Шредингера.

В уравнении Шредингера - оператор кинетической энергии, u – оператор потенциальной энергии.

Если потенциальная энергия u не зависит от времени, то полная энергия системы сохраняется.

Определение. Состояния системы, в которых ее энергия имеет определенное постоянное значение, называются стационарными состояниями.

Для стационарных состояний можно показать, что уравнение Шредингера принимает вид

(**)

Здесь Е – полная энергия системы.

Тогда , где - амплитудная волновая функция.

- плотность вероятности.

Тогда для стационарного случая .

Уравнения Шредингера для стационарного и нестационарного случая можно переписать в операторной форме: например, для стационарного случая уравнение принимает вид

,

где - дифференциальный оператор Гамильтона.

Уравнение (**) легко сводится к закону сохранения энергии.

Определение. Значения Е, при котором уравнение (**) имеет конечные, непрерывные и однозначные решения, называются собственными значениями энергии данной системы.

Поле изменения энергии включает две области:

1. E<0 – этим значениям Е соответствует дискретная совокупность состояний энергии;

2. E>0 – этой области соответствует непрерывный спектр.

Каждому собственному значению дискретного или непрерывного спектра энергии может соответствовать одна или несколько собственных функций. Если одному собственному значению соответствует несколько волновых функций, то такие состояния называются вырожденными. У вырожденных состояний каждому значению энергии соответствует несколько состояний. Число таких состояний называется кратностью вырождения или статистическим весом системы.

Вместо волновой функции Ψ (x,y,z,t) введем волновую функцию, описывающую состояние системы Ψ (x₁,y₁,z₁,…, x_i,y_i,z_i,…, x_n,y_n,z_n,t)= Ψ (…, x_i,y_i,z_i,…,t); вместо u введем потенциальную функцию (силовое поле): u(…, x_i,y_i,z_i,…,t). Массу микрочастиц обозначим m_j.

Обобщенное уравнение Шредингера для системы частиц:

iħ (*)

(**)

Полная энергия системы Е равна сумме энергий отдельных частиц, входящих в систему: .

Адиабатические и неадиабатические процессы.

В общем случае взаимодействия происходит изменение состояния ядер и электронов (причем взаимозависимо). Анализ показывает, что при определенных условиях движения электронов и ядер можно рассматривать раздельно. В этом случае из общего уравнения (*) можно выделить два уравнения, которые отдельно описывают движения ядер и электронов. Эти уравнения проще, чем (*).

Выясним условия, при которых (*) можно разделить на два уравнения. Обозначим Х совокупность всех координат ядер, , х совокупность всех координат электронов, . Для простоты полагаем массу всех ядер одинаковой (если система – многоатомная молекула, она состоит из одинаковых атомов).

iħ (*)

Предположение 1: предположим, что при фиксированных значениях Х электроны находятся в стационарном состоянии с энергией ε (ε – полная энергия подсистемы электронов). Если этот момент был начальным, то можно показать, что при перемещении ядер электроны могут оставаться в стационарном состоянии. Анализ показывает, что если скорости движения ядер много меньше скоростей движения электронов, v_я<<v_эл, то электроны при перемещениях ядер останутся в первоначальном стационарном состоянии. В реальных системах, состоящих из атомов и молекул, неравенство v_я<<v_эл, как правило выполняется. Например, для атома водорода v_эл10⁸ см/сек, для возбужденных состояний скорость выше. При этом, даже если молекулы движутся со скоростью звука, v_я~10⁵ см/сек.

Выделяя электронную подсистему, получим стационарное уравнение Шредингера, описывающее состояние этой системы.

(**)

Ψ (Х,х) – так называемые волновые функции. Х играет роль параметра. Предположим, что решение для (**) найдено, т.е. найден полный набор собственных значений энергии ε_k=ε_k(X), Ψ_k(X,x)=Ψ_k, k=1,2,… Математические свойства волновой функции Ψ (Х,х,t) и Ψ_k(X,x) таковы, что Ψ (Х,х,t) можно разложить в ряд Фурье по Ψ_k:

.

Подставим в таком виде Ψ (Х,х,t) в исходное уравнение (*). Умножим обе части уравнения на и проинтегрируем обе части уравнения (*) по всей области изменения х. Учитывая, что все стационарные функции Ψ_k и ортогональны и нормированы, получаем:

iħ

iħ =[

Предположение 2: предположим, что стационарные волновые функции Ψ_k(X,x) слабо зависят от координат ядер Х. В этом случае можно показать, что , и ей можно пренебречь. Тогда

iħ =[ . (***)

Формально это временное волновое уравнение, в котором роль волновой функции играет , а роль потенциальной функции выполняет . Это уравнение описывает нестационарное движение ядер в случае, если состояние электронов является стационарным.

состоит из потенциальной энергии взаимодействия всех ядер между собой, потенциальной энергии взаимодействия всех электронов между собой, потенциальной энергии взаимодействия всех электронов и всех ядер между собой и кинетической энергии всех электронов (но не ядер!).

Т.о, получили почти полное разделение движений ядер и электронов при предположении 2. Движения ядер и электронов полностью разделяются, их можно описать двумя уравнениями (для электронов (**), для ядер (***)).

Процессы, при которых такое разделение возможно, в квантовой механике называются адиабатическими процессами. Если электронные волновые функции Ψ_k сильно зависят от координат ядер, то ; в этом случае движения электронов и ядер не разделяются и для описания таких систем используется уравнение (*). Такие процессы в квантовой механике называются неадиабатическими.

Анализ показывает, что G→0 при медленной химической реакции; быстрые и очень быстрые реакции, как правило, неадиабатические.

Рассмотрим простейший случай состояния системы, описываемой обобщенной координатой Х (взаимодействуют два атома).

Адиабатическое движение – движение «вперед-назад» в рамках одного стационарного состояния. Вероятность нестационарного перехода электронов в новое стационарное состояние (вероятность неадиабатического процесса) = .

Случай классического движения ядер.

Предположим, что процесс адиабатичен: электроны описываются уравнением (**), ядра уравнением (***). При некоторых условиях можно заменить уравнение (***) уравнением Ньютона. В одномерном случае (двухатомная молекула):

, (****)

здесь , m₁, m₂ – масса ядер атомов, составляющих молекулу (в общем случае ).

Обозначим

Критерий возможности замены: ħ . Критерий выполняется тем лучше, чем меньше сила взаимодействия, чем больше масса ядер и чем быстрее они движутся. Таким условиям удовлетворяет идеальный газ. Для многоатомного случая критерий является необходимым, но не достаточным условием.

После нахождения вероятности химического взаимодействия находится средняя вероятность, которая является константой скорости химической реакции.

На основе классического представления о движении ядер разработаны 2 метода определения скорости химической реакции.

1. Основан на газокинетической теории мономолекулярных столкновений. Молекулы рассматриваются как упругие шарики, т.е. истинный характер потенциальной энергии взаимодействия не учитывается. При абсолютной упругости удара энергия взаимодействия скачком меняется от 0 до .

2. Метод переходного состояния (активированного комплекса). В данном методе молекулы не предполагаются как шары, а рассматриваются как реальные физические объекты; этот метод учитывает истинный характер потенциальной энергии взаимодействия.

Существуют и более сложные методы.

Общей чертой обоих методов является предположение, что химическая реакция не слишком сильно нарушает состояние термодинамического равновесия в системе (т.е. не слишком сильно нарушает равновесное распределение Максвелла-Больцмана для различных параметров).

Обмен энергии при соударении молекул. Условия сохранения равновесного распределения в реагирующей системе.

Предположим, что имеется некоторая идеальная газообразная система, в которой может происходить химическая реакция. Пусть до начала реакции в системе имело место равновесное распределение Максвелла-Больцмана.

Распределение Максвелла-Больцмана записывается по v_абс, v_отн, v_x, v_y, v_z. Удобно по v_отн: ; здесь n – общее число частиц в единице объема, m – масса частицы (приведенная масса), - число молекул в системе, относительные скорости которых лежат в интервале от v до v+dv.

Здесь v_m – наиболее вероятная скорость.

- вероятность того, что данная частица в системе имеет относительную скорость, лежащую в интервале от v до v+dv.

Увеличение температуры сдвигает v_m:

При увеличении температуры доля частиц с большими скоростями увеличивается, доля частиц с малыми скоростями уменьшается. Соударения со скоростью v v* будут химически эффективными (неупругое соударение с химической точки зрения).

Для идеального газа кинетическая энергия беспорядочного движения его частиц определяет внутреннюю энергию движения. Для реального газа нужно учитывать еще и потенциальную энергию взаимодействия.

Кинетическая энергия движущихся частиц: поступательные, вращательные, колебательные движения атомов; электронное движение (орбитальное и спиновое); движение нуклонов в ядре. Тогда внутренняя энергия . При адиабатических процессах отсутствуют, а не рассматриваем ввиду малости вклада в значение внутренней энергии.

Определение. Число степеней свободы f – число обобщенных координат, необходимых для полного описания положения тела в пространстве.

Рассмотрим различные системы, обладающие различным числом степеней свободы.

1. система является материальной точкой массы m. Тогда f=3 (пост. движения) (пространственные координаты x,y,z).

2. Система – абсолютно твердое тело (много точек, жестко связанных между собой). f =3 (пост.) + 3 (вращат.)=6

3. Система в целом газ, состоящий из N несвязанных частиц. f=3N=3 (пост.) + 3 (вращат.)+3N-6 (относит. движения)

4. N-атомная молекула: f=3N=3 (пост.) + 3 (вращат.)+3N-6 (колебания ядер в молекуле)

Частный случай: линейная N-атомная молекула: f=3 (пост.) + 3 (вращат.)+3N-5 (колебания ядер в молекуле)

Число колебательных степеней свободы представляется как 3N-6=(N-1) (деформационные колебания (меняются расстояния между ядрами) + (2N-5) (валентные колебания (изменение валентных углов).

Поступательному, вращательному, колебательному движению соответствует свой характер перемещений. Из статистической теории и эксперимента следует, что в системах, находящихся в равновесии, характеризующихся некоторой температурой и распределением Максвелла-Больцмана, распределение энергии по степеням свободы неравномерно. Приоритетом обладают поступательные степени свободы (всегда «заселены» энергией), затем вращательные (при низких температурах возможно отсутствие какого-либо типа вращений, в этом случае нет обеспечения энергией), затем колебательные (уже при средних температурах в меньшей степени обеспечены энергией). Это видно по зависимости теплоемкости от температуры:

В области очень высоких температур .

При столкновениях происходят превращения энергии из одних видов в другие. Легче всего трансформируется поступательная энергия во вращательную и колебательную; вероятность обратного перехода значительно меньше.

Превращения энергии происходят с различной вероятностью. Часть процессов выводит систему из равновесия, а часть возвращает в первоначальное равновесное состояние. Совокупность этих процессов называется процессами релаксации.

Рассмотрим химическую реакцию, протекающую по уравнению .

Пусть в начальный момент в обеих подсистемах (исходных частиц и конечных частиц) равновесие.

В результате прямой реакции (при T=const) в подсистеме исходных частиц доля богатых энергией молекул уменьшается (нарушение распределения Максвелла-Больцмана), а в подсистеме продуктов реакции число богатых энергией молекул увеличивается:

Для обратной реакции все происходит наоборот.

Тепловой эффект реакции приводит к нарушению распределения Максвелла-Больцмана (некоторый разогрев системы). Единого критерия до сих пор нет.

Химическая реакция – равновесный процесс, если она идет не слишком быстро.

Статистический метод расчета скорости химической реакции, основанный на газокинетической теории молекулярных столкновений.

Газокинетическая теория молекулярных столкновений (теория соударений).

Рассматривается реакция

	KII
А + В	→	продукты реакции

Согласно теории соударений, химическое взаимодействие имеет место при каждом соударении реагирующих частиц, обладающих достаточной энергией для преодоления потенциального барьера реакции и ориентированных должным образом относительно друг друга. Таким образом, скорость бимолекулярной реакции равна числу таких соударений реагирующих частиц в единице объема за единицу времени, при которых соударяющиеся частицы обладают энергией, достаточной для преодоления потенциального барьера реакции и ориентированных должным образом относительно друг друга.

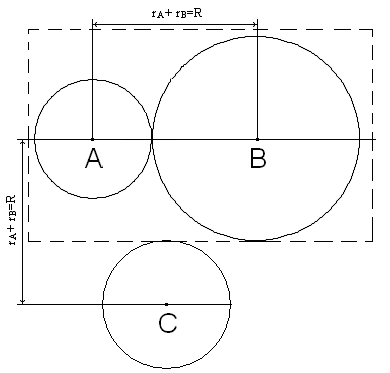
При рассмотрении процесса соударения двух частиц А и В они изображаются в виде двух шариков радиусов r_A и r_B. Используется система координат, связанная с одной из частиц (например, А).

- вектор скорости относительного движения в момент соприкосновения. При сближении частиц u_n не сохраняет значение и отвечающая ей кинетическая энергия ( ) переходит в потенциальную энергию (за счет чего: происходит торможение за счет действия кулоновских сил и дипольных сил отталкивания), а u_t может сохранить свое значение и не изменится.

Накопленная соударяющимися частицами потенциальная энергия может перейти обратно в кинетическую энергию поступательного движения в противоположном направлении. В этом случае произойдет отражение частицы В от А под углом, равным углу падения (т.е. произойдет упругое соударение частиц А и В). Однако накопленная потенциальная энергия может быть использована и на преодоление потенциального барьера химической реакции. Тогда произойдет химическое взаимодействие, т.е. неупругое соударение частиц А и В. Это возможно, когда будет больше некоторого минимального значения энергии, необходимого для преодоления кулоновских сил и дипольных сил отталкивания: (1).

Определение. Минимальная энергия в расчете на 1 моль, которой должны обладать частицы для того, чтобы вступить в химическую реакцию, называется энергией активации данной реакции.

Сечение соударения.

При соударении центры частиц оказываются на расстоянии r_A + r_B=R, поэтому соударение частиц А и В можно представить как соударение центра частицы В с воображаемой сферой радиуса r_A + r_B. Площадь сечения такой сферы называется сечением соударения. Сечение соударения частица А с частицами В дает отношение числа соударений в единицу времени частицы А с частицами В, движущимися в некотором определенном направлении, к величине потока, образуемого частицами В, т.е. к числу частиц В, проходящих в единицу времени через площадь 1 см², расположенную перпендикулярно направлению потока. Это сечение можно представить как площадь основания цилиндра, внутри которого движутся центры тех частиц, которые испытывают соударение с частицей А. Считая, что траектория частиц В вблизи А не искривляется, то о частицу А ударятся все частицы В, центры которых лежат внутри цилиндра с радиусом оси r_A + r_B и осью, параллельной направлению движения и проходящей через центр А (условие 1):

Число активных соударений.

Для получения выражения для скорости бимолекулярной реакции по теории соударений нужно найти число соударений в 1 см³ в секунду, удовлетворяющее неравенству (1). Это число называется числом активных соударений, z_a.

Полное число соударений молекул А с молекулами В в 1 см³ в секунду , где z_o – фактор соударений (вероятность соударения заданной частицы А с заданной частицей В, находящихся в пределах 1 см³, в течение секунды), n_A, n_B – концентрации молекул А и В (число А и В в единице объема).

Если рассматривать частицу А как неподвижную, то z_o – вероятность удара частицы В о частицу А. Т.к. все направления в пространстве эквивалентны, то для нахождения z_o можно ограничиться рассмотрением частиц, движущихся в определенном направлении: о частицу А ударяются только те частицы В, которые удовлетворяют условию 1.

Модель соударения А и В:

За время dt о частицу А ударятся только частицы В, находящиеся на расстоянии от А, меньшем, либо равном udt, т.е. частицы, находящиеся в пределах цилиндра объемом . За 1 сек: о частицу А ударятся только частицы В, находящиеся в пределах цилиндра объемом - эта величина есть вероятность соударения для частицы, имеющей относительную скорость u. Тогда , где - средняя относительная скорость движения частиц В, .

Для нахождения числа активных соударений нужно получить выражение для вероятности соударения частиц с нормальной составляющей скорости . Для этого нужно найти распределение соударяющихся частиц по нормальным скоростям. При рассмотрении учитываем только частицы, движущиеся в одном направлении. Величина u_n зависит от u и от расстояния r между траекторией частицы и осью соударения:

.

Распределение Максвелла-Больцмана по скоростям:

; по расстояниям (отношение площади кольцевого сечения , соответствующего расстоянию r от оси сечения, к площади сечения ). В силу независимости r и u распределение по обоим величинам имеет вид

.

Таким образом, вероятность соударения при относительной скорости u и расстоянии r между осью сечения и траекторией частицы В равна

.

Переходя от u к u_n и интегрируя по r от 0 до R, найдем вероятность соударения частицы со значением u_n в интервале u_n, u_n+d u_n:

Вероятность активного соударения:

Число активных соударений .

Стерический фактор. Скорость бимолекулярной реакции по теории соударений.

Согласно теории соударений, при активном соударении для того чтобы произошла химическая реакция, сталкивающиеся частицы не только должны обладать необходимым запасом энергии, но и должны быть определенным (благоприятным) образом ориентированы по отношению друг к другу. Вероятность того, что при столкновении частицы будут обладать необходимой для протекания реакции пространственной ориентацией, называется стерическим фактором (Р). Величина Р отражает вероятность благоприятного распределения энергии по степеням свободы в процессе столкновения. Поскольку энергетические и пространственные факторы действуют независимо, то число актов химического превращения в 1 см³ в единицу времени, т.е. скорость химической реакции . Для бимолекулярной реакции по закону действующих масс ; тогда .

В рамках газокинетической теории вычислить Р и Е невозможно; это квантовомеханическая задача, решаемая методом переходного состояния. На практике значение Е чаще всего определяется экспериментально.

Тройные соударения. Оценка скорости тримолекулярной реакции.

Рассматривается реакция

	KIII
А + В + С	→	продукты реакции

Существует математическая теория тройных соударений. Однако можно получить необходимый результат методом теории размерности.

Определение. Под тройным соударением подразумевают случай, когда 3 частицы расположены на расстоянии R, которое есть сумма радиусов любых двух частиц из числа сталкивающихся:

Средняя скорость относительного движения – средняя скорость теплового движения молекул . Средний тепловой пробег частицы , где n – концентрация, .

Величина R (обозначаемая также как d_o) называется газокинетическим диаметром столкновения.

Время соударения τ можно определить следующим образом: Можно свести тройные соударения к двойным столкновениям между квазимолекулой и обычной молекулой. Выделим конфигурацию, называемую квазимолекулой (пунктир на рис.); она имеет некоторое время жизни. Тогда τ~ . Введем t* - время между двумя последовательными соударениями; . Если давление и температура постоянны, то t*=const.

Отсюда вероятность тройного соударения f~ .

Тогда число тройных соударений .

Задача. 1) При давлении 1 атм и Т=300 К и концентрации частиц n=3·10¹⁹ см^-3 определить долю тройных соударений по отношению к двойным соударениям, .

2) при тех же условиях вычислить скорости бимолекулярной и тримолекулярной реакции , и сравнить их между собой.

3) определить критическое давление Р*, при котором , Т=const=300 К, .

При высоких давлениях столкновения становятся тройными.

Закон Аррениуса. Температурный коэффициент реакции. Экспериментальная энергия активации.

Закон Аррениуса – экспериментальный закон. Для бимолекулярной реакции было установлено, что , где z(T)~T^1/2.

Экспериментальное значение энергии активации Е_эксп обычно находится в диапазоне от 20 до 100 ккал/моль.

По углу наклона прямой определяем Е_эксп.

Если , то .

Аррениус предложил следующую схему химической реакции, введя понятия исходного состояния (исходный состав системы, Р, Т), переходного состояния, конечного состояния (конечный состав, Р, Т):

Недостаток схемы: нет определяющей величины по оси х. Е₁ и Е₂ – энергии активации для прямой и обратной реакции, Q – тепловой эффект химической реакции.

По схеме Аррениуса прямая реакция – экзотермическая, обратная – эндотермическая.

В соответствии со схемой для прямой реакции , для обратной реакции .

Отсюда, вычитая из первого уравнения второе, получаем: - уравнение Вант-Гоффа: .

Введем понятие температурного коэффициента химической реакции: - отношение констант скоростей одной и той же химической реакции при двух температурах, различающихся на 10 К: .

При средних температурах =2-4; =5-7 – низкие температуры; →1 – высокие температуры, Т→ .

Дома: построить график (Т).

При высоких температурах скорость химической реакции перестает зависеть от Т.

Еще одно определение : .

В широком интервале температур энергия активации может зависеть от температуры:

По своему смыслу . Для простой одностадийной реакции не может быть <1. Если выявляется, что <1, то механизм реакции сложный.

Введение экспериментальной энергии активации.

Из газокинетической теории (1)

Экспериментальный закон Аррениуса (2)

Чтобы ввести в теоретическую формулу (1) экспериментальное значение энергии активации вместо теоретического, нужно слить кривые 1 и 2.

, Т_о – параметр, T₁<T_o<T₂.

Чтобы слить кривые, необходимо равенство логарифмических производных:

.

Выразим Е_теор через Е_эксп; подставляя полученное выражение в формулу (1), получаем (3)

Формула (3) отличается от (1) только множителем ; им можно пренебречь и просто заменить Е_теор на Е_эксп. Этот вывод справедлив, если вводим Е_эксп в формулу, полученную из газокинетической теории. Более точный результат дает метод переходного состояния.

Теория переходного состояния, или активированного комплекса.

Потенциальная энергия системы атомов.

Пусть система состоит из N частиц; число степеней свободы f=3N. Считаем, что частицы являются свободными атомами, точнее, под N подразумеваем ядра атомов.

3N-6 – число степеней свободы относительного перемещения ядер в системе, 3 вращательных, 3 колебательных степени свободы.

Если система линейна, то число степеней свободы относительного перемещения ядер в системе 3N-5.

Потенциальная энергия взаимодействия: ε= ε (X₁,X₂,…,X_3N-6) для общего случая, ε=ε (X₁,X₂,…,X_3N-5) для линейного случая. Т.к. ε – многомерная функция, то с геометрической точки зрения зависимость ε от координат представляет собой многомерную поверхность. Характерное для этой поверхности в случае химически реагирующих систем: на топологической карте поверхности есть потенциальные ямы, разделенные барьерами, переход через которые соответствует химической реакции. В настоящее время эта задача точно решена для систем из 3 и 4 атомов, но выводы, полученные при решении этих задач, являются общими для любого числа атомов.

Выводы: 1) появляется возможность составить общую качественную картину движения всех атомов в потенциальном поле ε; 2) исследовать механизм передачи и превращения энергии при столкновении атомов в системе; 3) определить, какая геометрическая конфигурация этой системы наиболее выгодна для осуществления химической реакции; 4) уточнить физический смысл переходного состояния; 5) вычислить теоретическую энергию активации.

Рассмотрим систему трех атомов, расположенных на одной линии:

В этом случае N=3. Число степеней свободы относительного движения f_отн=3N-5=4.

В общем случае из (3N-6) степеней свободы (N-1) – перемещения вдоль линий связи (валентные колебания), (2N-5) – перемещения поперек линий связи (деформационные колебания). В линейном случае системы трех атомов получается 2 валентных колебания и 2 деформационных колебания. Деформационные колебания считаются замороженными.

Чем обусловлен выбор линейной системы из 3 атомов: можно построить график ε=ε (X_АВ,X_ВС). Переменные могут меняться от 0 до ∞, но мы ограничим область их изменения областью, на которой энергия имеет характерный вид (с потенциальными ямами и барьерами). Для построения топографической карты проведем секущие плоскости. Каждая линия на топографической карте соответствует определенному значению ε.

В нуле при приближении Х_АВ и Х_ВС к 0 ε→∞ (острый пик в 0).

(А+ВС): А не оказывает влияния на ВС;

(АВ+С): С не оказывает влияния на АВ.

линия водораздела (если поместить в (*) источник воды, то вода потекла бы по ). (*) – седловинная точка.

линия перевала.

Проведем анализ характерных сечений. Каждому сечению соответствует конкретный тип взаимодействия.

Сечение 1-1: Х_ВС=const (велико), 0≤X_AB<∞.

Для системы 3-х атомов ситуация означает, что атом С далеко от В и стоит на месте, а расстояние между А и В меняется произвольно. Потенциальной яме в сечении 1-1 соответствует двухатомная молекула АВ и независимый атом С.

Проведем сечение 2-2: Х_АВ=const (велико), 0≤X_BС<∞.

Потенциальной яме в сечении 2-2 соответствует двухатомная молекула ВС и независимый атом А.

Сечение 3-3: Х_АВ меняется слабо, 0≤X_BС<∞.

Эта кривая соответствует процессу упругого столкновения молекулы АВ и атома С, образования новых частиц не происходит. При сближении АВ и С энергия возрастает.

Сечение 4-4: Х_ВС меняется слабо, 0≤X_AB<∞. Двигаться начинаем из района верхней потенциальной ямы.

Эта кривая соответствует процессу упругого столкновения молекулы ВС и атома А, образования новых частиц не происходит. При сближении А и ВС энергия возрастает.

Проведем сечение 5-5. 0≤Х_АВ, X_BС<∞.

Сечение близко к обеим потенциальным ямам. Пойдем по сечению сверх вниз.

На рис. - обобщенная координата, называемая профилем пути реакции. Уровни минимумов отличаются. По существу, получили схему Аррениуса.

Это сечение соответствует прямой реакции А+ВС АВ+С. Если бы пошли в обратную сторону, получим обратную реакцию.

характеризует глубину превращения системы. Процесс 5-5 пошел бы с минимальной энергией, если бы мы пошли по «линии водораздела».

Выделенное красным «плато» соответствует ситуации, когда все три атома находятся на бесконечном расстоянии друг от друга и не взаимодействуют.

Примем условно за исходное состояние АВ+С. Идем до седловиной точки по линии водораздела, а затем идем по линии перевала до выделенного красным плато: процесс: АВ+С→А+В+С – диссоциация молекулы АВ.

D₁ – энергия связи в молекуле АВ; D₂ – энергия связи в молекуле ВС.

Можно пойти из состояния А + ВС по аналогичному пути. Процесс – диссоциация ВС: А+ВС→А+В+С.

На основе анализа можно определить геометрическую конфигурацию переходного активированного комплекса. Для рассматриваемого случая переходной активированный комплекс – трехатомная линейная молекула.

Рассмотрим теперь систему трех атомов, не находящихся на одной прямой:

Здесь три независимых переменных. Нарисовать картину в декартовых координатах нельзя, но применяемый анализ аналогичен.

В этом случае появляются промежуточные потенциальные ямы, соответствующие т.н. метастабильным состояниям:

Аналогичная картина получается и для систем четырех атомов, находящихся и не находящихся на одной прямой. При этом установлено, что конфигурация переходного комплекса для системы четырех атомов, не лежащих на одной прямой, плоская:

Качественное рассмотрение превращения энергии в системе 3-х атомов.

Полная энергия системы . При адиабатических процессах отсутствует, а не рассматриваем ввиду малости вклада в значение внутренней энергии (т.е. состояние ядер не затрагивается). Для системы трех атомов, лежащих на одной прямой, . не будет, т.к. все атомы фиксированы на одной прямой.

Введем новые переменные х=х(Х_АВ,Х_ВС), у=у(Х_АВ,Х_ВС). При проведении замены переменных получаем, что кинетическая энергия системы , где  - приведенная масса, . После замены переменных получается та же топографическая карта для энергии системы, что и ранее в криволинейных координатах.

По сути, всю систему представили как шарик массы , без трения катающийся по «энергетической» поверхности.

Рассмотрим изменения его кинетической и потенциальной энергии, которые соответствуют изменениям энергии в системе.

Пусть исходное состояние АВ+С. Система – «шарик» обладает некоторым запасом энергии (помещаем шарик в некоторое устройство и выстреливаем его). Шарик покатится по некоторой гладкой траектории. Если общего запаса энергии недостаточно для выхода из ямы, шарик обратно скатывается по периодической траектории:

Эта ситуация соответствует процессу АВ+С → АВ* +С, где АВ* - колебательно возбужденная молекула. Часть кинетической энергии превращается в колебательную энергию молекулы АВ.

Шарик некоторое время будет колебаться вокруг «дна» ямы. Процесс: АВ*+С → АВ + С:

Колебательно возбужденная молекула АВ* отдает энергию, колебания полностью или частично затухают.

Пусть теперь запаса кинетической энергии хватает для преодоления потенциального барьера, но траектория идет не по линии водораздела.

АВ+С → А + ВС* (колебательно возбужденная молекула).

Пусть запаса кинетической энергии достаточно для преодоления потенциального барьера, но недостаточно для того, чтобы реакция прошла до конца:

АВ+С → [A…B…C]* → AB* + C

Наличие дополнительных ям резко увеличивает возможность возврата. Все зависит от перераспределения энергии по степеням свободы. Различают благоприятное и неблагоприятное перераспределение.

Переходной комплекс:

4 степени свободы

₁ – характеристическая частота этого валентного колебания

₂ – характеристическая частота этого валентного колебания, .

- частоты, соответствующие этим двум типам деформационных колебаний, равны, т.к. направления по осям y и z равноправны.

Внутренняя энергия активированного комплекса под действием случайных причин может распределиться по всем степеням свободы или сконцентрироваться на какой-то одной степени свободы.

Степень свободы с частотой ₂ выгодна.

Концентрация энергии на этой степени свободы выгодна. Если есть несколько выгодных степеней свободы, то реакция может пойти по разным путям.

Выгодные степени свободы дают реакцию, невыгодные не дают реакции.

Расчет скорости химической реакции методом переходного состояния.

В методе подсчитывается число изобразительных точек, пересекающих за единицу времени линию перевала вблизи седловинной точки. Это число отождествляется со скоростью химической реакции.

Метод связывает скорость реакции с формой потенциальной поверхности. Метод активированного комплекса позволяет рассчитать скорость реакции, если из эксперимента известны параметры, характеризующие потенциальную поверхность.

Основным уравнением метода активированного комплекса является уравнение, связывающее константу скорости со свойствами переходного состояния.

Пусть δ – область состояний вблизи вершины потенциального барьера, которую можно рассматривать как переходное состояние. Для большинства элементарных реакций система, пришедшая в переходное состояние, неизбежно перейдет в конечное состояние, т.е. перевалит через барьер: маловероятно, что энергия системы равна - энергии переходного состояния. Если энергия системы хоть немного меньше , система не достигнет переходного состояния. Если энергия системы хоть немного больше , система перейдет в переходное состояние с некоторым запасом кинетической энергии, поэтому перевалит через барьер.

Переходному состоянию приписывается некоторая протяженность δ вдоль пути реакции. Система проходит участок δ за некоторый конечный интервал времени τ. Если в некоторый момент времени в системе имеется активированных комплексов в единице объема, то в единицу времени в продукты реакции перейдет активированных комплексов. Количество молекул продуктов реакции, образовавшееся в единице объема в единицу времени, есть в то же время скорость реакции, которая, следовательно, оказывается равной . Таким образом, задача определения скорости реакции (следовательно, и константы скорости реакции) сводится к определению времени τ, необходимому для прохождения переходного состояния, и концентрации активированных комплексов .

τ равно отношению длины отрезка δ к средней скорости прохождения через переходное состояние : . Прохождение через переходное состояние можно рассматривать как поступательное движение системы вдоль координаты реакции. Число частиц dN, скорость которых вдоль направления Х лежит в интервале u_x, u_x+du_x, определяется формулой кинетической теории газов: , N – общее число частиц, m – масса частиц. Тогда по правилу определения среднего .

Следовательно, .

При определении в методе активированного комплекса допускают, что переход активированных комплексов в продукты реакции не нарушает распределение Максвелла-Больцмана в системе. Это означает, что восстановление этого распределения, нарушаемого расходованием активированных комплексов, происходит значительно быстрее, чем само химическое превращение. При таком допущении можно выразить через концентрации реагирующих частиц, нулевые энергии и статистические суммы активированного комплекса и реагирующих частиц. Активированный комплекс в этом случае можно рассматривать как квазичастицу, составленную определенным образом из частиц А, В, …

Из статистической физики известно, что , где с_А, с_В, … - концентрации частиц А,В,… (в числе частиц в единице объема), Е – разность нулевых энергий активированного комплекса и исходных частиц (энергия активации), z_A, z_B, … - статистические суммы исходных частиц; - статистическая сумма активированного комплекса. Активированный комплекс отличается от обычных частиц тем, что перемещению вдоль одной его степени свободы, а именно вдоль координаты реакции Х, соответствует максимум энергии. Поэтому (произведение статистических сумм для перемещения вдоль координаты Х и для совокупности всех остальных степеней свободы). Если рассматривать перемещение вдоль координаты реакции как поступательное движение на отрезке протяженностью δ, то . Тогда .

Отсюда . Константа скорости реакции определяется как - основная формула метода активированного комплекса.

При выводе формулы предполагалось, что, пройдя через барьер, система не может вернуться в исходное состояние. Между тем, если в реакции образуется одна частица с достаточно большим запасом энергии, она может вновь оказаться в переходном состоянии и после этого вернуться в исходное состояние. Эта возможность исчезает только когда система дезактивируется в результате соударений с другими частицами, и ее энергия будет меньше . Вероятность возврата в исходное состояние тем больше, чем меньше давление (уменьшается число соударений между молекулами).

В неадиабатических процессах и процессах, идущих с образованием одной частицы при малых давлениях, нужно учитывать вероятность того, что система, достигнув переходного состояния, перейдет через него (κ). κ называется коэффициентом прохождения, или трансмиссионным коэффициентом. Тогда .

Для определения статистических сумм нужно знать молекулярные веса, моменты инерции и частоты колебаний исходных молекул и активированного комплекса.

Для реакции вида .

Статистические суммы.

Статистическая физика изучает состояние систем, состоящих из большого числа частиц. Пусть в такой системе N частиц. Уравнение, определяющее состояние системы – распределение Гиббса: вероятность того, что подсистема из N частиц находится в состоянии с энергией Е, Е+dE, - для непрерывного изменения энергии. Здесь d - статистический вес системы (кратность вырождения – число состояний с данной энергией). z – статистическая сумма, характеризующая состояние системы. Если энергия меняется непрерывно, то . p_i – обобщенный импульс, q_i – обобщенная координата.

Если изменение энергии в подсистеме дискретно, то , .

Можно показать, что если N=1, то распределение Гиббса-Гельмгольца переходит в распределение Максвелла-Больцмана: .

Если , то . Если и не рассматриваются, то

Пусть подсистема – N-атомная молекула. Полное число степеней свободы Если считать, что все степени свободы физически однородны (равноценны), то ; аналогично можно расписать статистические суммы для вращательных и колебательных степеней свободы.

1. Поступательное движение: ħ². Тогда , V=1.

Для поступательного движения кратность вырождения равна 1. .

2. Для вращательных степеней свободы: рассматриваем квантовый ротатор:

Для него E_{вращ j}= ħ²j(j+1)/2I, I=

В рассматриваемом случае I_x=0, I_y=I_z=I, где I главный момент инерции в декартовой системе координат; (Е_вращ)=2j+1. Для двух степеней свободы / ħ², для одной степени свободы / ħ.

В общем случае для многоатомной молекулы / ħ³, где  - параметр симметрии, I_i – главные моменты инерции в декартовой системе координат.

3. Для колебательного движения: рассматривается квантовый осциллятор:

Пусть колебания гармонические. Тогда , где V – колебательное квантовое число, V=0,1,2,…

. Обычно , и можно разложить в ряд Тейлора:

.

Для многоатомной молекулы , =1,…,3N-6.

Применение статистических сумм для расчета скоростей химических реакций.

При выводе формулы одна колебательная степень свободы уже взята; эта степень свободы соответствует ; поэтому содержит на одну колебательную степень свободы меньше, чем , …

1. Мономолекулярные реакции.

	KI
А	→	продукты реакции

Нужно рассчитать K_I .

Для оценки можно воспользоваться тем, что молекула достаточно жесткая; тогда статистические суммы попарно сократятся, а .

Тогда

2. Бимолекулярные реакции.

	KII
А + В	→	продукты реакции

а) А и В – одноатомные молекулы, А⁽¹⁾, В⁽¹⁾, с массами m_A, m_B.

А⁽¹⁾ + В⁽¹⁾ → [AB]* → AB

;

т.к. взаимодействуют две одноатомные молекулы, то переходным комплексом будет двухатомная молекула (это единственная возможность).

Тогда .

Обозначим .

Если эффективное сечение соударения , то

.

Поскольку , то из сравнения с газокинетической теорией получаем, что Р1. Вывод: любое соударение с энергией, равной или превышающей значение энергии активации, будет химически эффективным, а факторы, связанные с перераспределением энергии по степеням свободы, отсутствуют.

б) А – одноатомная молекула, А⁽¹⁾, В – двухатомная молекула, В⁽²⁾, с массами m_A, m_B.

	KII
А(1) + В(2)	→	продукты реакции

Т.к. в реакции участвуют три атома, то активированный комплекс – нелинейная в общем случае трехатомная молекула.

;

.

Перепишем выражение для К_II в виде

;

обозначим - стерический фактор.

Тогда .

Оценим значение стерического фактора. При средних температурах , . Тогда Р₁₂~10^-1-10^-2. Тип реакции тот же, что и для случая а), но Р меньше в 10-100 раз, т.е. если взять все столкновения с достаточной энергией, то из-за неблагоприятного перераспределения энергии по степеням свободы только одно из 10-100 столкновений будет химически эффективным.