4. Примеры выполнения задания.
4.1. Пример 1.
Имея в точке А скорость vA мотоцикл поднимается τ секунд по участку АВ длиной l, составляющему с горизонтом угол α. При постоянной на всем участке АВ движущей силе Р мотоцикл в точке В приобретает скорость vВ и перелетает через ров шириной d, находясь в воздухе Т сек и приземляясь в точке С со скоростью vС. Масса мотоцикла с мотоциклистом равна m. При решении задачи считать мотоцикл с мотоциклистом материальной точкой и не учитывать сил сопротивления движению.
Рис. 2
Дано: α=30°; vA=0; Р=2 кН; d=4 м; h=1,5 м; l=40 м
Определить: Т и m .
Решение.
Изображаем действующие на материальную
точку активные силы – силу тяжести
,
силу
;
силы реакции связей – сила
- нормальная реакция опорной поверхности.
,
т.к. задано в условии не учитывать сил
сопротивления движению.
Рассмотрим движение на участке АВ. Система координат y1Аx1, время движения в данной системе – τ (с).
Записываем второй закон Ньютона в
векторной форме:
.
Проецируем на координатную ось Ах1
Разделим левую и правую часть на массу, получим дифференциальное уравнение второго порядка и начальные условия
Начальные условия:
и
При t=τ
;
по условию задачи
или
Рассмотрим движение на участке ВС. Система координат yBx; время движения Т.
Записываем второй закон Ньютона в
векторной форме:
Проецируем на координатную ось Вх
Начальные условия
Начальные условия
Проецируем на координатную ось Ву
Начальные условия
Начальные условия
4.2. Пример 2.
Дано: f=0,25; l=4м; d=3м; h=5м
Определить:
и
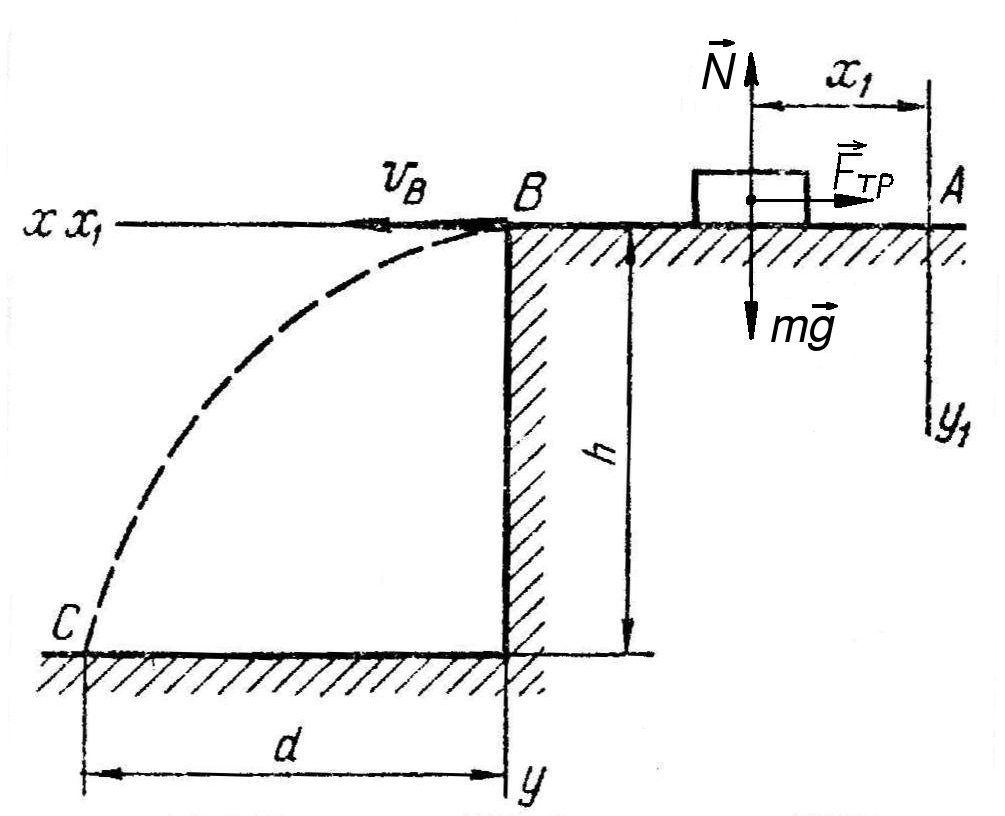
Рис. 3
Указываем действующие силы:
на участке АВ на материальную точку действуют:
- активная сила ,
- реакции связей: - нормальная реакция опорной поверхности,
- сила трения, направленная в сторону,
противоположную движению.
Записываем второй закон Ньютона в дифференциальной форме для оси Ах1:
(1)
где f – коэффициент трения скольжения,
N – нормальная реакция опорной поверхности определяется из условия равновесия (движения вдоль оси Ау1 нет).
Значит сумма проекций всех действующих сил на ось Ау1 равна 0.
Ау1:
подставим в уравнение (1)
После сокращения на массу m получим исходное уравнение для интегрирования:
После интегрирования получим:
Определим С1 исходя из начальных условий:
Таким образом
Для определения значения скорости vB подставляем время - время движения по участку АВ из в :
(1а)
Интегрируя второй раз, получим:
С2 определяем исходя из начальных условий: расстояние х1 для момента времени t=0 будет равно 0
Для определения длины участка АВ-l подставим значение
(1б)
В уравнениях (1а) и (1б) неизвестных три:
и
.
Количество неизвестных превышает
количество уравнений. Продолжаем решение
для нахождения
из второй части задачи.
Во второй части задачи движение происходит вдоль осей Вх и Ву.
Записываем второй закон Ньютона в дифференциальной форме для оси Вх:
- не действуют никакие силы
интегрируем первый раз
(2а)
интегрируем второй раз
При значении t=T
– время движения по участку ВС
(2б)
Записываем второй закон Ньютона в дифференциальной форме для оси Ву:
Интегрируем первый раз, получим
Определим С5 :
Интегрируя второй раз, получим
Определим С6 :
При значении
Вычислим значение
Принимаем
Из уравнения (2б) находим
При найденном значении решаем уравнения (1а) и (1б)
(1а)
(1б)
подставим в (1б)
Определяем значение времени движения по участку АВ, решая квадратное уравнение относительно через дискриминант. Учитываем только положительное значение .
Определяем
Ответ:
;
4.2. Пример 2.
В железнодорожных скальных выемках для защиты кюветов от попадания в них с откосов каменных осыпей устраивается «полка» DC. Учитывая возможность движения камня из наивысшей точки А откоса и полагая при этом его начальную скорость равной нулю, определить минимальную ширину полки b и скорость , с которой камень падает на неё. По участку АВ откоса, составляющему угол с горизонтом и имеющему длину l, камень движется сек.
При решении задачи считать трения скольжения f камня на участке АВ постоянным, а сопротивлением воздуха пренебречь.
Дано:
=0;
;
l=4 м;
сек; f≠0; h=5
м;
.
Определить b и .
Решение.
Рассмотрим движение камня на участке
АВ. Принимая камень за материальную
точку, покажем (см. Рис. 4) действующие
на него силы: вес
,
нормальную реакцию
и силу трения скольжения
.
Составим дифференциальное уравнение
движения камня на участке АВ:
;
.
Сила трения
,
где
.
Таким образом,
или
.
Интегрируя дифференциальное уравнения дважды, получаем:
,
.
Для определения постоянных интегрирования
воспользуемся начальными условиями
задачи: при t=0 x10=0
и
.
Составив уравнение, полученное при
интегрировании, для t=0
,
,
Найдём постоянные:
,
.
Тогда
;
.
Для момента , когда камень покидает участок,
;
,
т.е.
,
,
откуда
,
т.е.
м/сек.
Рассмотрим движение камня от точки В до точки С.
Показав силу тяжести , действующую на камень, составим дифференциальные уравнения его движения:
,
.
Интегрируем первое из этих уравнений:
,
.
Постоянные интегрирования С3 и
С4 определим, используя начальные
условия задачи: при t=0
x0=0,
.
С помощью уравнений, полученных при интегрировании и составленных для t=0,
,
,
найдём, что
;
.
Тогда
,
.
Интегрируя уравнение , имеем:
,
.
Начальные условия: при t=0
y0=0,
.
Из уравнений, полученных интегрированием
и составленных для t=0,
,
,
найдём, что
и
.
Окончательно
,
.
Таким образом, уравнения движения камня имеют вид
;
.
Уравнение траектории камня найдем, исключив параметр t из уравнений движения. Определив t из первого уравнения и подставив его значение во второе, получаем уравнение параболы:
.
В момент падения
м, а
,
т.е.
,
откуда
,
так что
м,
м.
Поскольку траекторией движения камня является вервь параболы с положительными абсциссами её точек, то d=2,11 м.
Минимальная ширина полки
м.
Используя уравнение движения камня , найдём время Т движения камня от точки В до точки С:
,
откуда
сек.
Скорость камня при падении найдём через проекции скорости на оси координат:
,
по формуле
.
Для момента падения (t=Т=0,53 сек)
м/сек.