
- •Кафедра физики введение в физику
- •1. Общие методические указания к выполнению контрольных работ
- •Контрольная работа №1 (№2) По дисциплине «Введение в физику» Вариант № 1
- •Задачи к контрольной работе №1 по дисциплине «Введение в физику»
- •Перечень тем к контрольной работе № 2 по дисциплине «Введение в физику»
- •2. Основы векторной алгебры и математического анализа
- •2.1. Скалярные и векторные величины
- •2.2. Действия с векторами
- •2.2.1 Сравнение векторов
- •2.2.2 Сложение векторов
- •Правило параллелограмма для сложения двух векторов:
- •Правило треугольника для сложения двух векторов:
- •2.2.3 Вычитание векторов
- •Правило параллелограмма.
- •Правило треугольника.
- •2.2.4 Умножение вектора на скаляр
- •2.3. Скалярное и векторное произведения
- •2.3.1 Скалярное произведение
- •2.3.2 Векторное произведение
- •2.4. Производная и интеграл
- •2.4.1. Производная и ее применения
- •Cписок производных простейших элементарных функций
- •2.4.2. Первообразная и интеграл
- •Список основных неопределенных интегралов
- •3.Задания для контрольной работы по дисциплине «Введениие в физику»
- •3.1. Основы векторной алгебры
- •3.2. Прямая задача кинематики Векторный способ описания движения частицы
- •Координатный способ описания движения частицы
- •3.3. Обратная задача кинематики
- •3.4. Связь линейных и угловых величин в кинематике
- •3.5. Кинематика вращательного движения
- •3.6. Сила как причина изменения импульса
- •3.7. Динамика вращательного движения твердого тела
- •3.8. Момент инерции. Теорема Штейнера. Центр масс
- •Теорема Штейнера.
- •3.9. Кинетическая энергия. Мощность. Работа
- •3.10. Закон сохранения импульса и момента импульса
- •Литература
3.9. Кинетическая энергия. Мощность. Работа
Кинетическая
энергия катящегося тела
![]() ,
где
,
где
![]() –
скорость центра масс тела,
–
скорость центра масс тела,
![]() – момент инерции тела относительно оси
вращения, проходящей через центр масс,
– момент инерции тела относительно оси
вращения, проходящей через центр масс,
![]() – угловая скорость вращения.
– угловая скорость вращения.
Мощность
![]() ,
где
– скорость перемещения точки приложения
силы.
,
где
– скорость перемещения точки приложения
силы.
Работа
силы
![]() ,где
,где
![]() – перемещение,
– угол между вектором силы и вектором
перемещения,
– перемещение,
– угол между вектором силы и вектором
перемещения,
![]() .
.
Работа
момента силы
![]() .
.
9-1.
Шарик массы m
и
радиуса R
катится по горизонтальной поверхности
со скоростью
![]() без проскальзывания. Найдите кинетическую
энергию этого шарика. m
= 1
кг, R
=
1 м,
без проскальзывания. Найдите кинетическую
энергию этого шарика. m
= 1
кг, R
=
1 м,
![]() м/с.
м/с.
9-2. Диск массы m и радиуса R катится по горизонтальной поверхности со скоростью без проскальзывания. Найдите кинетическую энергию этого диска. m = 1 кг, R = 1 м, м/с.
![]() 9-3.
Катушка без ниток имеющая массу m,
внешний радиус R
и момент инерции I,
катится
по горизонтальной поверхности со
скоростью
без проскальзывания. Найдите кинетическую
энергию этой катушки. m
= 1
кг, R
=
1 м, I
=
1
,
м/с.
9-3.
Катушка без ниток имеющая массу m,
внешний радиус R
и момент инерции I,
катится
по горизонтальной поверхности со
скоростью
без проскальзывания. Найдите кинетическую
энергию этой катушки. m
= 1
кг, R
=
1 м, I
=
1
,
м/с.
9-4.
Небольшое тело начало движение из начала
координат вдоль горизонтальной оси х
под
действием силы, направленной под углом
= 30
к оси х.
Модуль силы меняется в зависимости от
координаты х
по
закону
![]() .
Найти работу этой силы на участке пути
от
.
Найти работу этой силы на участке пути
от
![]() .
А
=
1 Н, b
= 1 м.
.
А
=
1 Н, b
= 1 м.
9-5.
Небольшое тело начало движение из начала
координат вдоль горизонтальной оси х
под
действием силы, направленной под углом
к оси х.
Модуль силы F
не
меняется, но угол
зависит от координаты х
по
закону
![]() .
Найти работу этой силы на участке пути
от
,
если b
= 1 м, F
= 1 Н, А
=
0,25 Н,
.
Найти работу этой силы на участке пути
от
,
если b
= 1 м, F
= 1 Н, А
=
0,25 Н,
9-6.
Найти работу, произведенную машиной за
промежуток времени
с, если мощность машины зависит от
времени по закону
![]() .
Если
с, А
=
1 Вт.
.
Если
с, А
=
1 Вт.
9-7.
Массивный диск может вращаться вокруг
закрепленной оси без трения. Найдите
работу момента силы при повороте диска
на угол
,
если момент сил, действующий на диск,
зависит от угла поворота
![]() по закону
по закону
![]() ,
если А
=
1
,
если А
=
1
![]() ,
,
![]() рад.
рад.
![]() 9-8.
Тело движется вдоль горизонтальной оси
х
под действием силы
,
направленной под углом
к оси х.
В некоторый момент тело достигает
скорости
.
Найдите мощность силы в этот момент
времени. F
=
1 Н,
м/с,
= 30.
9-8.
Тело движется вдоль горизонтальной оси
х
под действием силы
,
направленной под углом
к оси х.
В некоторый момент тело достигает
скорости
.
Найдите мощность силы в этот момент
времени. F
=
1 Н,
м/с,
= 30.
![]() 9-9.
Тонкий однородный стержень массы m
и длины l
может вращаться вокруг горизонтальной
оси, проходящей через конец стержня.
Стержень привели в горизонтальное
положение и толкнули так, что незакрепленный
конец стержня приобрел скорость
.
Найдите кинетическую энергию стержня
в первый момент времени. m
=1
кг, l
=
1 м,
м/с.
9-9.
Тонкий однородный стержень массы m
и длины l
может вращаться вокруг горизонтальной
оси, проходящей через конец стержня.
Стержень привели в горизонтальное
положение и толкнули так, что незакрепленный
конец стержня приобрел скорость
.
Найдите кинетическую энергию стержня
в первый момент времени. m
=1
кг, l
=
1 м,
м/с.
9-10. Шарик массы m и радиуса R катится без проскальзывания по горизонтальной поверхности, вращаясь с угловой скоростью . Найдите кинетическую энергию этого шарика. m = 1 кг, R = 1 м, = 1 рад/с.
3.10. Закон сохранения импульса и момента импульса
При взаимодействии частиц системы между собой полный вектор импульса системы остается постоянным в случаях, когда
а)
![]() ,
б)
,
б)
![]() и время взаимодействия очень мало. В
этих случаях
и время взаимодействия очень мало. В
этих случаях
![]() ,
где
,
где
![]() – векторная
сумма
импульсов частиц, которые существовали
до взаимодействия,
– векторная
сумма
импульсов частиц, которые существовали
до взаимодействия,
![]() – векторная
сумма
импульсов всех частиц, которые будут
существовать после взаимодействия.
Если
– векторная
сумма
импульсов всех частиц, которые будут
существовать после взаимодействия.
Если
![]() ,
то сохраняется только проекция
полного импульса
системы
на ось x,
,
то сохраняется только проекция
полного импульса
системы
на ось x,
![]() .
.
При взаимодействии частиц системы между собой полный вектор момента импульса системы остается постоянным в случаях, когда
а)
![]() ,
б)
,
б)
![]() и время взаимодействия очень мало. В
этих случаях
и время взаимодействия очень мало. В
этих случаях
![]() где
где
![]() – векторная
сумма моментов импульсов
частиц, которые существовали до
взаимодействия,
– векторная
сумма моментов импульсов
частиц, которые существовали до
взаимодействия,
![]() – векторная
сумма моментов импульсов
всех частиц, которые будут существовать
после взаимодействия. Если
– векторная
сумма моментов импульсов
всех частиц, которые будут существовать
после взаимодействия. Если
![]() ,
то сохраняется только
проекция момента импульса
системы на ось z
,
то сохраняется только
проекция момента импульса
системы на ось z
![]() (часто относительно закрепленной оси
вращения).
(часто относительно закрепленной оси
вращения).
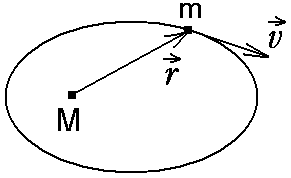
Момент
импульса частицы
![]() ,
где
– радиус-вектор частицы,
,
где
– радиус-вектор частицы,
![]() – импульс частицы.
– импульс частицы.
![]() ,
где
– угол между
и
,
где
– угол между
и
![]() .
Для твердого тела, вращающегося вокруг
закрепленной оси z
,
где
– момент инерции тела относительно оси
z,
.
Для твердого тела, вращающегося вокруг
закрепленной оси z
,
где
– момент инерции тела относительно оси
z,
![]() – угловая скорость.
– угловая скорость.
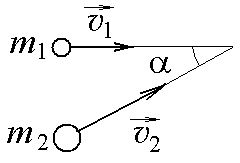 10-1.
Маленький пластилиновый шарик массы
m1
движется горизонтально со скоростью
10-1.
Маленький пластилиновый шарик массы
m1
движется горизонтально со скоростью
![]() .
Под углом
к направлению его движения летит второй
шарик массы m2
со скоростью
.
Под углом
к направлению его движения летит второй
шарик массы m2
со скоростью
![]() и сталкивается с первым. Шарики слипаются
и движутся под углом
к первоначальному направлению движения
второго шарика. Найдите
и сталкивается с первым. Шарики слипаются
и движутся под углом
к первоначальному направлению движения
второго шарика. Найдите
![]() .
Если
.
Если
![]() 1 кг,
1 кг,
![]() 2 кг,
2 кг,
![]() 1 м/с,
1 м/с,
![]() 2 м/с,
= 30.
2 м/с,
= 30.
10-2.
Маленький пластилиновый шарик массы
m1
движется горизонтально со скоростью
.
Под углом
к направлению его движения летит второй
шарик массы m2
со скоростью
и сталкивается с первым. Шарики слипаются
и движутся под со скоростью
![]() .
Найдите после удара модуль импульса
шариков. Если
1 кг,
2 кг,
1 м/с,
2 м/с,
= 45.
.
Найдите после удара модуль импульса
шариков. Если
1 кг,
2 кг,
1 м/с,
2 м/с,
= 45.
10-3. Маленький пластилиновый шарик массы m1 движется горизонтально со скоростью . Перпендикулярно к направлению его движения летит второй шарик массы m2 со скоростью и сталкивается с первым. Шарики слипаются и далее движутся вместе. Найдите после удара а) модуль импульса шариков; б) модуль скорости шариков. Если 1 кг, 2 кг, 1 м/с, 2 м/с.
10-4.
Маленький пластилиновый шарик массы
m1
движется горизонтально со скоростью
.
Перпендикулярно к направлению его
движения летит второй шарик массы m2
со скоростью
и сталкивается с первым. Шарики слипаются
и далее движутся вместе под углом
к первоначальному направлению движения
первого шарика шарика. Найдите
![]() и
и
![]() .
Если
1 кг,
2 кг,
1 м/с,
2 м/с.
.
Если
1 кг,
2 кг,
1 м/с,
2 м/с.
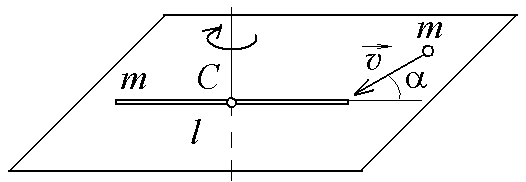 10-5.
На горизонтальной плоскости лежит
тонкий однородный стержень массы m
=1 кг и длины l,
который может вращаться вокруг
вертикальной оси, проходящей через
центр масс стержня С.
Под углом
=30
к стержню в той же плоскости движется
маленький пластилиновый шарик такой
же массы m
со скоростью
=
1 м/с. Шарик прилипает к концу стержня,
и система приобретает угловую скорость
вращения .
Найти угловую скорость вращения системы
после удара, если l
=
1 м.
10-5.
На горизонтальной плоскости лежит
тонкий однородный стержень массы m
=1 кг и длины l,
который может вращаться вокруг
вертикальной оси, проходящей через
центр масс стержня С.
Под углом
=30
к стержню в той же плоскости движется
маленький пластилиновый шарик такой
же массы m
со скоростью
=
1 м/с. Шарик прилипает к концу стержня,
и система приобретает угловую скорость
вращения .
Найти угловую скорость вращения системы
после удара, если l
=
1 м.
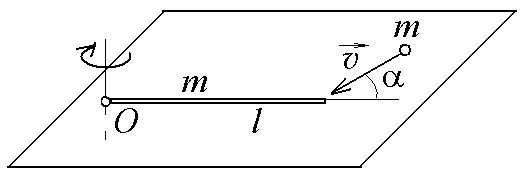 10-6.
На горизонтальной плоскости лежит
тонкий однородный стержень массы m
=1 кг и длины l,
который может вращаться вокруг
вертикальной оси, проходящей через
конец стержня О.
Под углом
=30
к стержню в той же плоскости движется
маленький пластилиновый шарик такой
же массы m
со скоростью
=
1 м/с. Шарик прилипает к концу стержня,
и система приобретает угловую скорость
вращения .
Найти угловую скорость вращения системы
после удара, если l
=
1 м.
10-6.
На горизонтальной плоскости лежит
тонкий однородный стержень массы m
=1 кг и длины l,
который может вращаться вокруг
вертикальной оси, проходящей через
конец стержня О.
Под углом
=30
к стержню в той же плоскости движется
маленький пластилиновый шарик такой
же массы m
со скоростью
=
1 м/с. Шарик прилипает к концу стержня,
и система приобретает угловую скорость
вращения .
Найти угловую скорость вращения системы
после удара, если l
=
1 м.
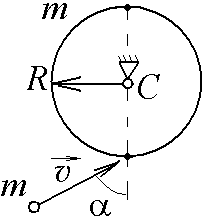 10-7.
Тонкий однородный диск массы m
= 1 кг и радиуса R
может вращаться в вертикальной плоскости
вокруг горизонтальной оси, проходящей
через его центр С.
Под углом
=30
к вертикали в плоскости вращения диска
движется маленький пластилиновый шарик
такой же массы m
со скоростью
=
1 м/с. Шарик прилипает к нижней точке
неподвижно висящего диска, и система
приобретает угловую скорость вращения
w..
Найти угловую скорость вращения системы
после удара, если R
=
1 м.
10-7.
Тонкий однородный диск массы m
= 1 кг и радиуса R
может вращаться в вертикальной плоскости
вокруг горизонтальной оси, проходящей
через его центр С.
Под углом
=30
к вертикали в плоскости вращения диска
движется маленький пластилиновый шарик
такой же массы m
со скоростью
=
1 м/с. Шарик прилипает к нижней точке
неподвижно висящего диска, и система
приобретает угловую скорость вращения
w..
Найти угловую скорость вращения системы
после удара, если R
=
1 м.
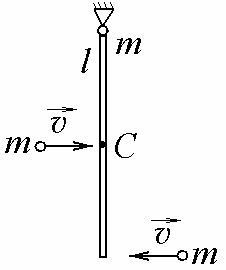 10-8.
Тонкий однородный стержень массы m
= 1 кг и длины l
может вращаться в вертикальной плоскости
вокруг горизонтальной оси, проходящей
через его конец. С разных сторон на
стержень горизонтально в той же плоскости
налетают два одинаковых пластилиновых
шарика той же массы m
с одинаковыми скоростями
= 1 м/с. Первый шарик застревает в центре
стержня, второй – в нижнем конце, и
система приобретает угловую скорость
.
Найти угловую скорость вращения системы
после удара, если l
=
1 м.
10-8.
Тонкий однородный стержень массы m
= 1 кг и длины l
может вращаться в вертикальной плоскости
вокруг горизонтальной оси, проходящей
через его конец. С разных сторон на
стержень горизонтально в той же плоскости
налетают два одинаковых пластилиновых
шарика той же массы m
с одинаковыми скоростями
= 1 м/с. Первый шарик застревает в центре
стержня, второй – в нижнем конце, и
система приобретает угловую скорость
.
Найти угловую скорость вращения системы
после удара, если l
=
1 м.
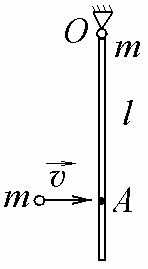 10-9.
Тонкий однородный стержень массы m
=1 кг и длины l
может вращаться в вертикальной плоскости
вокруг горизонтальной оси, проходящей
через его конец O.
Горизонтально в той же плоскости на
стержень налетает пластилиновый шарик
той же массы m
со скоростью
=
1 м/с. Шарик застревает в точке А
стержня
на расстоянии х=
10-9.
Тонкий однородный стержень массы m
=1 кг и длины l
может вращаться в вертикальной плоскости
вокруг горизонтальной оси, проходящей
через его конец O.
Горизонтально в той же плоскости на
стержень налетает пластилиновый шарик
той же массы m
со скоростью
=
1 м/с. Шарик застревает в точке А
стержня
на расстоянии х=
![]() от точки О,
и система приобретает угловую скорость
.
Найти угловую скорость вращения системы
после удара, если l
=
1 м.
от точки О,
и система приобретает угловую скорость
.
Найти угловую скорость вращения системы
после удара, если l
=
1 м.
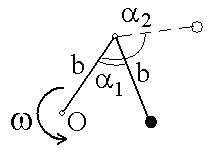 0-10.
Два невесомых стержня длины b
соединены под углом 1
= 60
и вращаются без трения в горизонтальной
плоскости вокруг вертикальной оси О с
угловой скоростью
= 2 рад/с. На конце одного из стержней
прикреплен очень маленький массивный
шарик. В некоторый момент угол между
стержнями самопроизвольно увеличился
до 2
= 120.
С какой угловой скоростью стала вращаться
такая система?
0-10.
Два невесомых стержня длины b
соединены под углом 1
= 60
и вращаются без трения в горизонтальной
плоскости вокруг вертикальной оси О с
угловой скоростью
= 2 рад/с. На конце одного из стержней
прикреплен очень маленький массивный
шарик. В некоторый момент угол между
стержнями самопроизвольно увеличился
до 2
= 120.
С какой угловой скоростью стала вращаться
такая система?
