Определение необходимой численности выборки

Необходимая численность выборки при повторном отборе для выборочной средней рассчитывается как:

, (9.14)

Необходимая численность выборки при повторном отборе для выборочной доли рассчитывается как:

, (9.15)

Необходимая численность выборки при бесповторном отборе рассчитывается как:

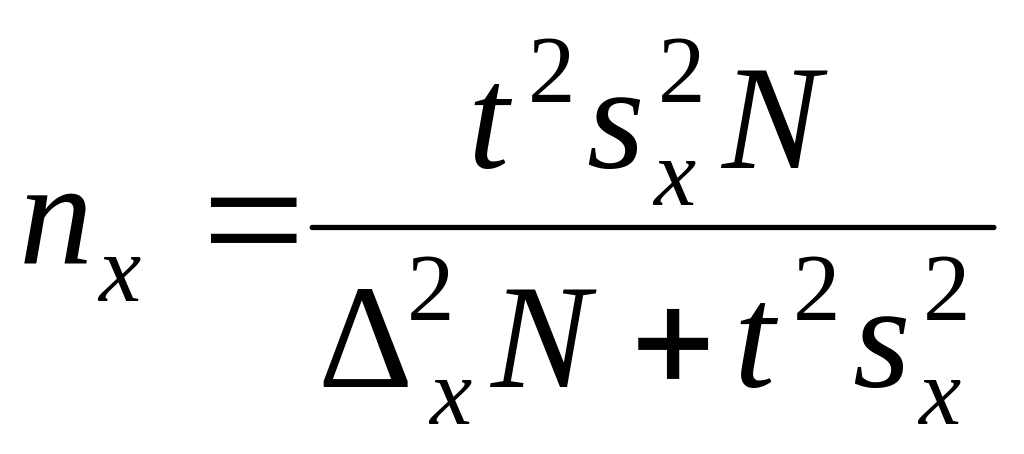, (9.16)

Необходимая численность выборки при бесповторном отборе рассчитывается как:

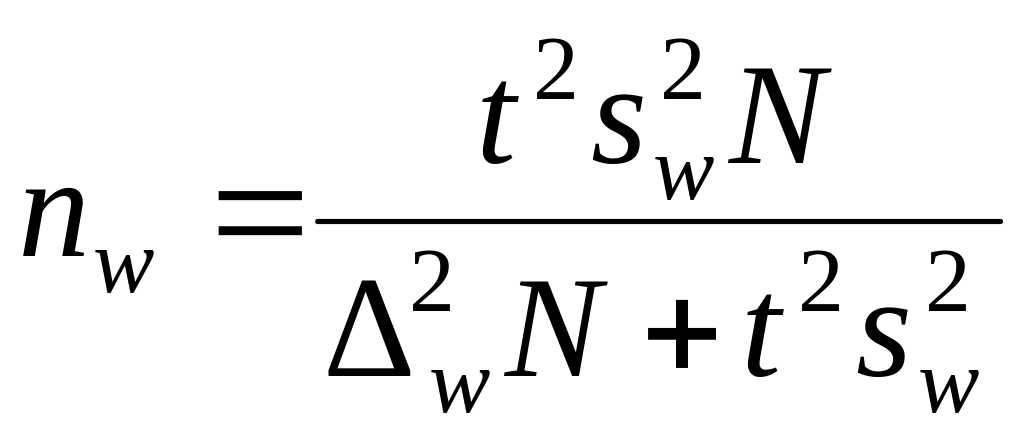, (9.17)

Малая выборка – выборка, объем которой не превышает 20 единиц.

Средняя ошибка малой выборки рассчитывается как:

, (9.18)

где – дисперсия малой выборки.

, (9.19)

Предельная ошибка малой выборки определяется как:

(9.20)

В малых выборках коэффициент доверия зависит не только от заданной доверительной вероятности. Согласно распределению Стьюдента, вероятность того, что предельная ошибка не превысит среднюю ошибку, зависит и от величины , и от численности выборки n. Для отдельных значений и n доверительная вероятность малой выборки рассчитывается по специальным таблицам Стьюдента, в которых даны распределения стандартизированных отклонений:

Способы распространения характеристик выборки на генеральную совокупность

Способ прямого пересчета – показатели выборочной доли или средней распространяются на генеральную совокупность с учетом ошибки выборки.

Способ поправочных коэффициентов – после обобщения данных сплошного учета практикуется 10%-е выборочное обследование с определением так называемого «процента недоучета».

Таблица 37

Распределение вероятности в малых выборках в зависимости от значения коэффициента доверия и численности выборки

	5	7	10	12	16	18	20
1	0,626	0,644	0,656	0,662	0,666	0,668	0,670
1,5	0,792	0,816	0,832	0,838	0,846	0,848	0,850
2,0	0,884	0,908	0,924	0,930	0,936	0,938	0,940
2,5	0,933	0,953	0,966	0,970	0,975	0,977	0,978
3	0,960	0,976	0,984	0,988	0,991	0,992	0,992

Пример 20. Для определение средних затрат рабочего времени на 1ц. продукции растениеводства была проведена 5% выборка в которую попало 35 хозяйств специализированных на производство зерна. Установлено, что средние затраты труда на производство 1ц. продукции составляют 14,8ч.-часа, при Необходимо определить среднюю и предельную (с вероятностью 0,954 (при )) ошибку выборки для случайного бесповторного отбора, повторить для случайного повторного отбора.

Решение.

Средняя ошибка выборочной средней при случайном бесповторном отборе:

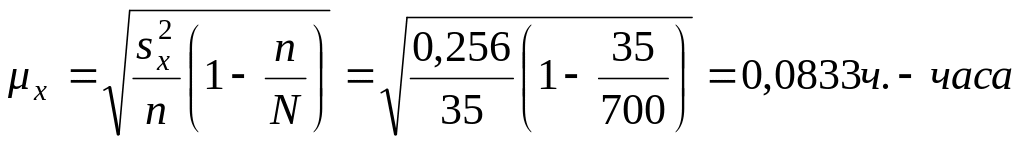
При бесповторном отборе предельная ошибка выборочной средней определяется как:

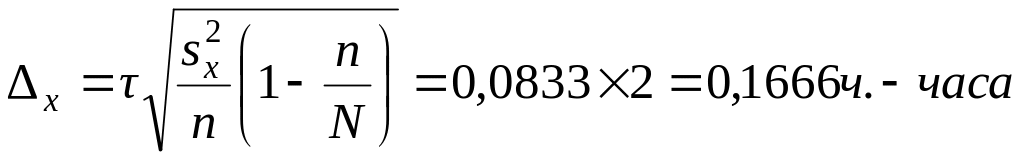
То есть, с вероятностью 0,954, можно сказать, что средние затраты рабочего времени на 1ц. продукции растениеводства находятся в пределах

Средняя ошибка при случайном повторном отборе выборочной средней рассчитывается по формуле:

.

При повторном отборе предельная ошибка выборочной средней определяется как:

.

То есть, с вероятностью 0,954, можно сказать, что средние затраты рабочего времени на 1ц. продукции растениеводства находятся в пределах

Расчет по бесповторной модели всегда точнее.

Пример 21. Методом бесповторного отбора из общей численности молочного стада была проведена 5% выборка в которую попало 200 голов. Результаты показали, что 30% коров в выборке старше 5 лет. Определить с вероятностью 0,7699 пределы, в которых находится доля коров старше 5 лет, дисперсия доли

Решение.

Средняя ошибка выборочной доли определяется:

При бесповторном отборе предельная ошибка для выборочной доли определяется как:

.

То есть, с вероятностью 0,7699 можно утверждать, что доля коров старше 5 лет составляет .

Пример 22. Молочное стадо КРС в районе составляет 15000голов. Необходимо определить численность выборки, в которой с вероятностью 0,9109 предельная ошибка среднего надоя не должна превышать 0,2 кг при среднем квадратическом отклонении надоя 1,2кг.

Решение. Численность выборки при бесповторном отборе определяется как:

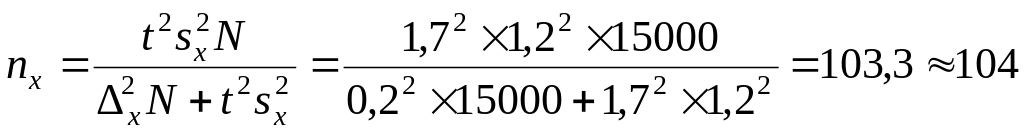
Проведем проверку:

Средняя ошибка:

Предельная ошибка выборочной средней при вероятности 0,9109 ( ) что не превышает заданной ошибки предельной ошибки 0,2кг.

Пример 23. В районе среди 11000 частных индивидуальных хозяйств изучается доля хозяйств с числом голов КРС две и более на одно хозяйства.

Необходимо определить необходимую численность выборки для бесповторного и повторного отборов с вероятностью 0,6827( ) и ошибкой выборки доли хозяйств, с числом голов три и более, не превышающей 0,03, известно, что дисперсия равна 0,4.

Решение.

1. для бесповторного отбора

2. для повторного отбора