12.1.3. Понятие предела переменной. Производная функции. Таблица производных. Правила дифференцирования

Переменная величина может изменяться так, что в процессе возрастания или убывания она приближается к некоторой конечной постоянной величине, которая является ее пределом.

По определению пределом переменной величины х называется постоянная величина А, к которой х в процессе своего изменения приближается так, что модуль разности между x и А, т.е. | х - А |, стремится к нулю.

Обозначения предела: x→ А или lim x = A (здесь «→» – знак предельного перехода, lim от лат. limited, в переводе на русский – предел). Рассмотрим элементарный пример:

x : 0,9; 0,99; 0,999; 0,9999…→ 1, A = 1(lim x = 1), т.к.

| х - А |: 0,1; 0,01; 0,001; 0,0001…→ 0.

Введем понятия приращение аргумента и приращение функции. Если переменная величина х изменяет свое значение от x₁ до х₂, то разность x₂ – x₁ = Δx называется приращением аргумента. Соответствующее изменение функции y₂ – y₁ = Δy называется приращением функции. Покажем это на графике функции y = f(x) (рис. 12.2). Геометрически приращение аргумента изображается приращением абсциссы точки кривой, а приращение функции - приращением ординаты этой точки.

П роизводной заданной функции y = f(x) по аргументу х называется предел отношения приращения функции Δу к приращению аргумента Δх, вычисленный при условии, что Δх → 0 .

Она обозначается или , или dy/dx (читается «дэ y по дэ x»). Таким образом, производная функции y = f(x) равна:

(12.5)

Правило для отыскания производной функции у = f(х) по аргументу х содержится в определении этой величины: нужно задать приращение аргумента Δх, найти приращение функции Δy, составить отношение и найти предел этого отношения при Δх→ 0.

Процесс нахождения производной называется дифференцированием функции. Этим занимается раздел высшей математики называемый «Дифференциальное исчисление».

Таблица производных основных элементарных функций, полученных по указанному выше правилу, приведена ниже (табл. 12.1)

Таблица 12.1

№ п/п	Виды функции	Производная функции
1	Постоянная величина y = c	y' = 0
2	Степенная функция y = xn (n может быть положительным, отрицательным, целым, дробным)	y' = nxn-1
3	Показательная функция y = ax (a > 0; a ≠ 1) y = ex y = e-x	y' = axln a y' = ex y' = - e-x
4	Логарифмическая функция y = logax (a > 0; a ≠ 1) y = ln x	y' = y' =
5	Тригонометрические функции: y = sin x y = cos x y = tg x y = ctg x	y' = cos x y' = - sin x y' = y' = -

Если выражение, производную которого надо найти, представляет собой сумму, разность, произведение или частное нескольких функций, например, u, v, z, то используются нижеследующие правила дифференцирования (табл. 12.2).

Таблица 12.2

1. y = u + v – z	1) y' = u' + v' - z'
2. y = u · v	2) y = u' · v + v '· u
3. y =	3) y' =
4. y = a · u, где a = const	4) y' = a · u'

Приведем несколько примеров вычисления производных, используя табл. 12.1 и табл. 12.2

1. (x + sin x )' = (x)' + (sin x)' = 1 + cos x;

2. (x · sin x )' = (x)' · sin x + x · (sin x)' = sin x + x cos x;

3. ;

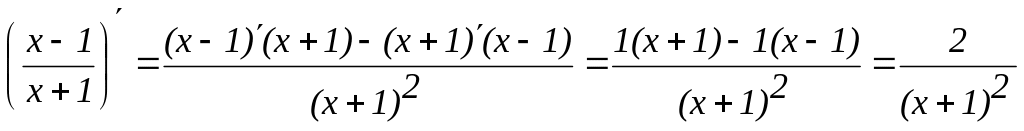4. (5 tgx)' = 5 (tg x)' = .