- •Розглянуто
- •Одеса – 2012
- •Тема 1. Загальні поняття про систему лінійних рівнянь.
- •Тема 2. Матриці, види матриць, дії з матрицями.
- •Контрольна робота Правила виконання контрольної роботи
- •Завдання для контрольної роботи
- •2. Обчислити визначник матриці а.
- •3. Знайти матрицю а-1, обернену до матриці а
- •Приклад розв’язання завдання 2
2. Обчислити визначник матриці а.
Розв’язання: Обчислимо визначник за допомогою алгебраїчних доповнень.
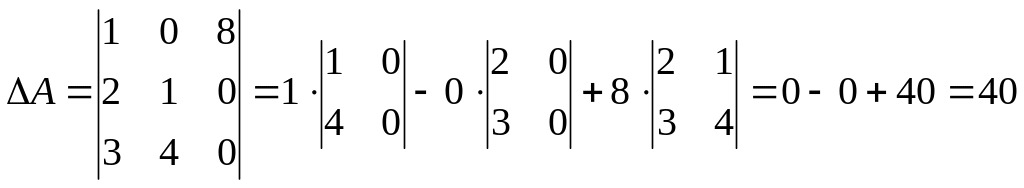 .
.
3. Знайти матрицю а-1, обернену до матриці а
Розв’язання: Для знаходження оберненої матриці використаємо формулу:
![]() ,
,
де А - приєднана до А матриця, складена з алгебраїчних доповнень елементів матриці А, символ Т позначає операцію транспортування.
а)
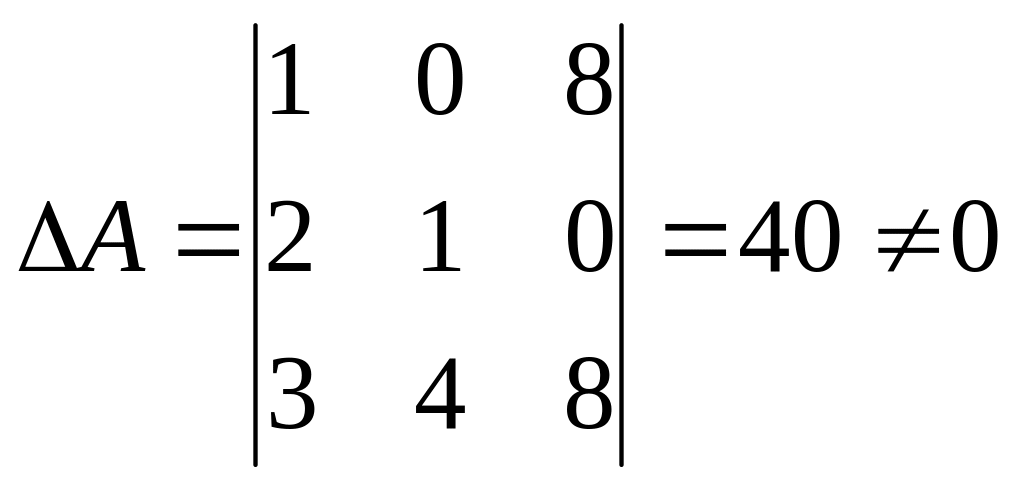 ,
,
отже, матриця А невироджена, тобто, вона має обернену.
б) Обчислимо алгебраїчні доповнення елементів матриці А:
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]()
![]() ,
,
![]() ,
,
![]() .
.
Тоді,
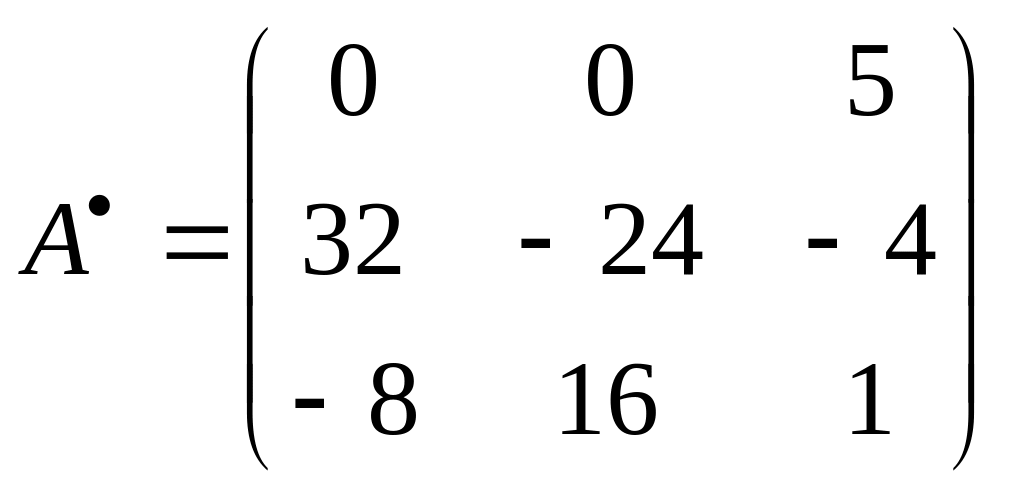 .
.
Отже
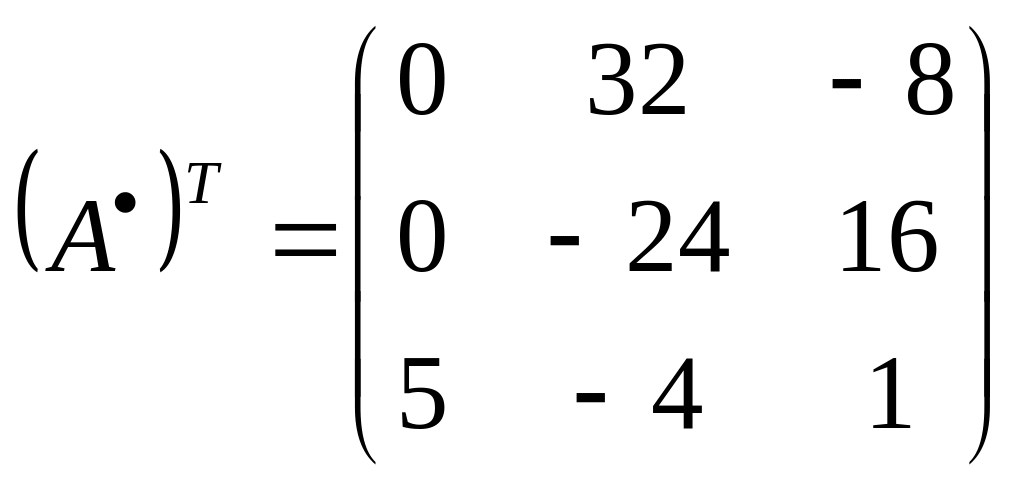
в) Отримаємо обернену матрицю
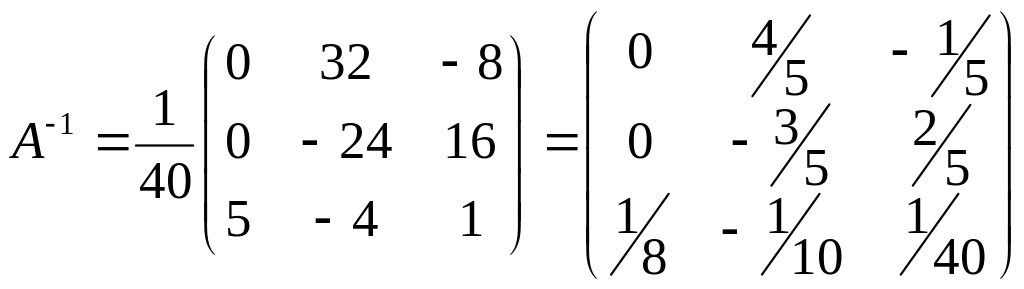
г) Впевнимось, що А-1 – обернена матриця до А.
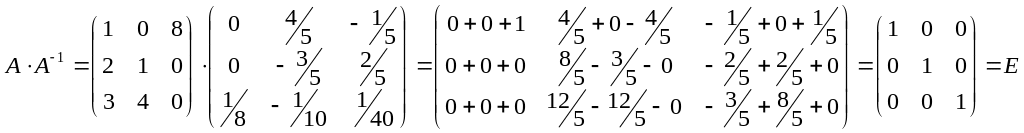
Таким
чином, матриця
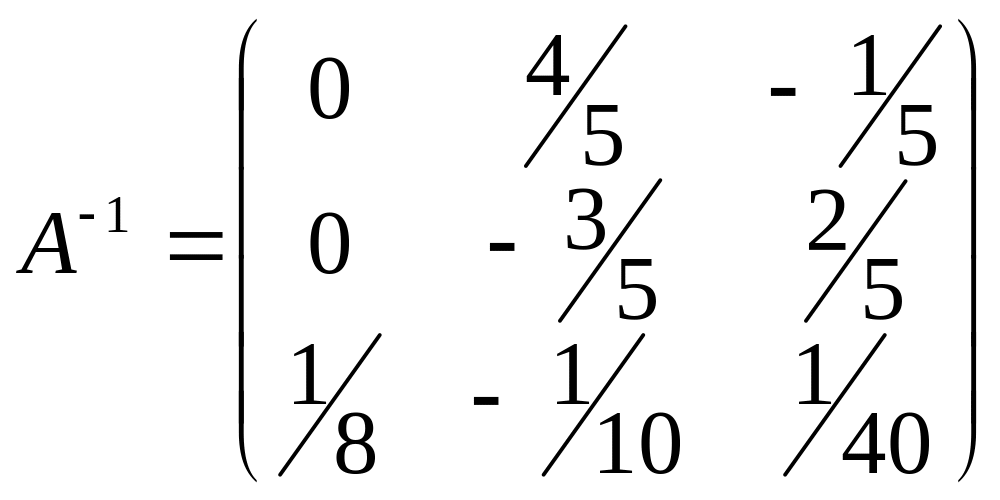 є оберненою до матриці А.
є оберненою до матриці А.
4. Розв’язати матричне рівняння A*X=B.
Розв’язання: Помножимо обидві частини рівняння А*Х=В на А-1 зліва
тобто
А-1А*Х=А-1*В, або Х=А-1*В.
Таким чином, для розв’язку задачі необхідно побудувати матрицю А-1 обернену до матриці А.
З попередньої задачі маємо
.
Тоді розв’язком матричного рівняння буде матриця:
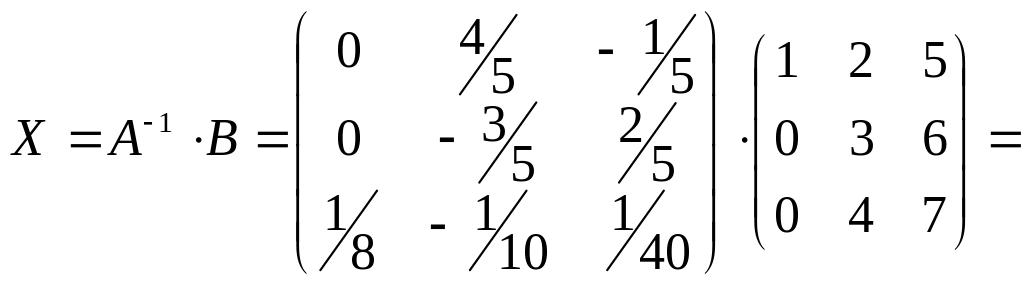
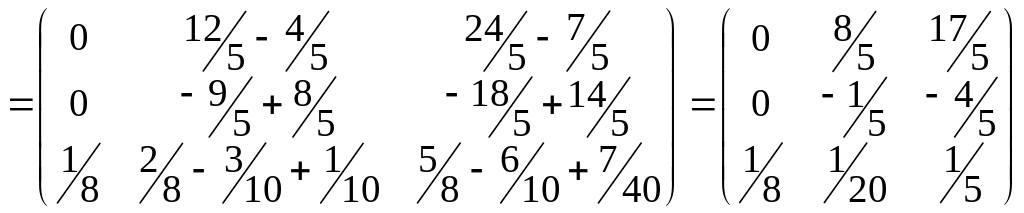
5. Розв’язати систему рівнянь
![]()
а) Методом Крамера
Розв’язання:
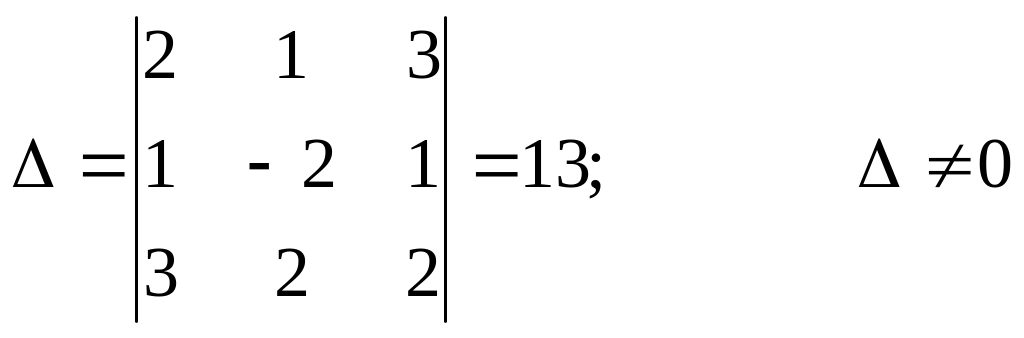
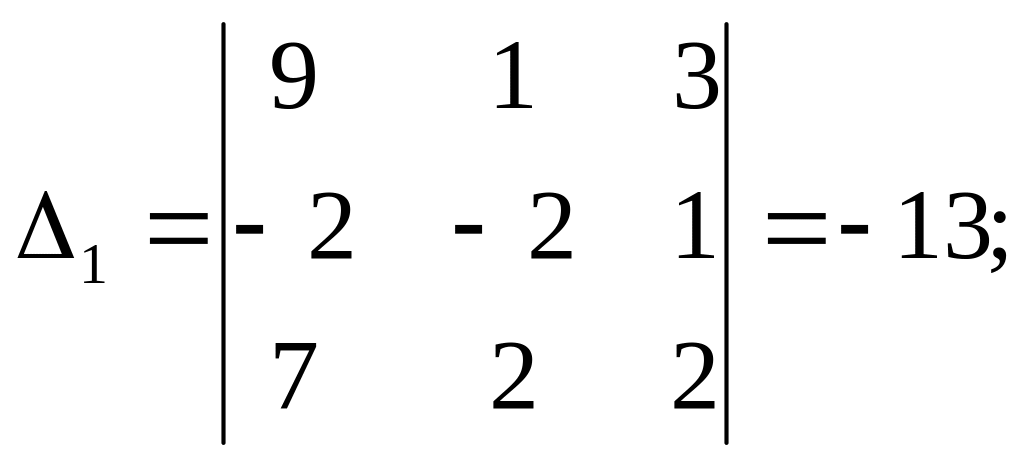

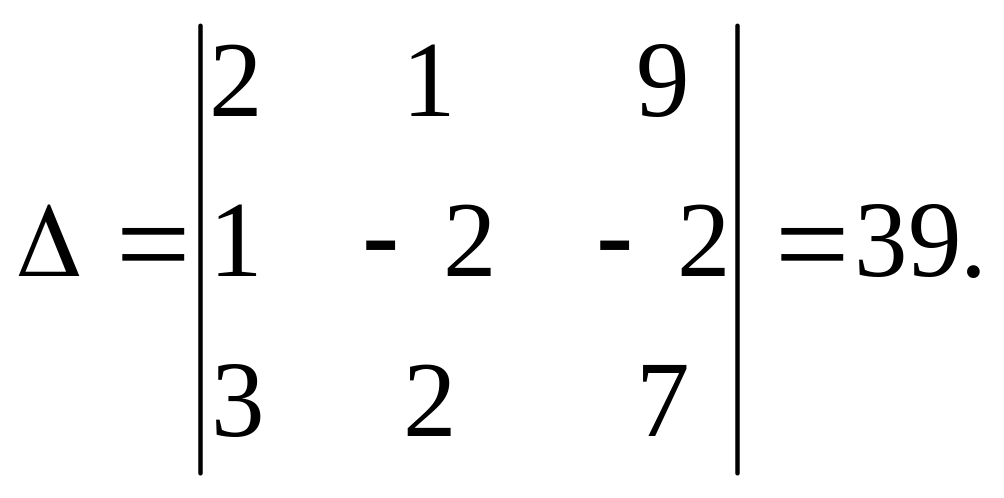
Тоді:
![]()
![]()
![]()
б) Методом Гаусса
Розв’язання:
Складемо розширену матрицю системи та приведемо її до трикутної за допомогою елементарних перетворень.
А=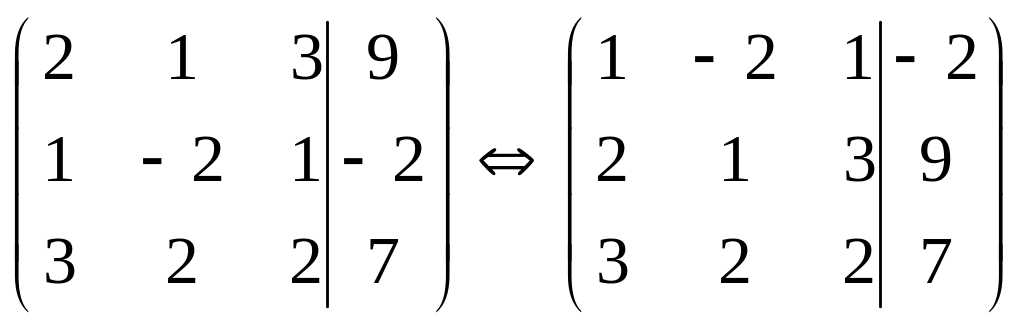 .
.
Від другого рядка матриці віднімемо перший рядок помножений на 2, а від третього рядка віднімемо перший помножений на 3:
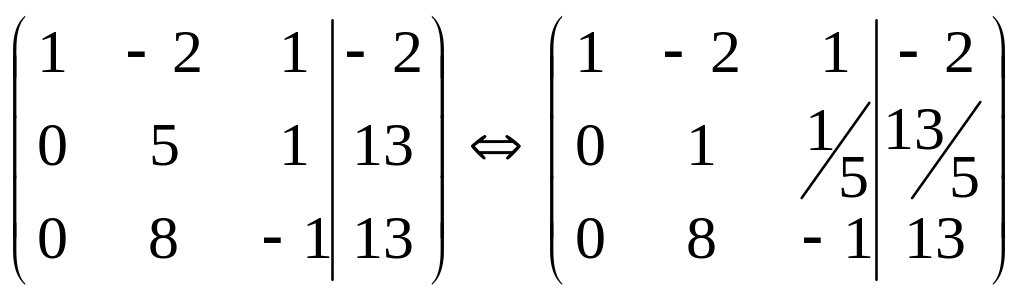 .
.
Від третього рядка віднімемо другий помножений на 8:
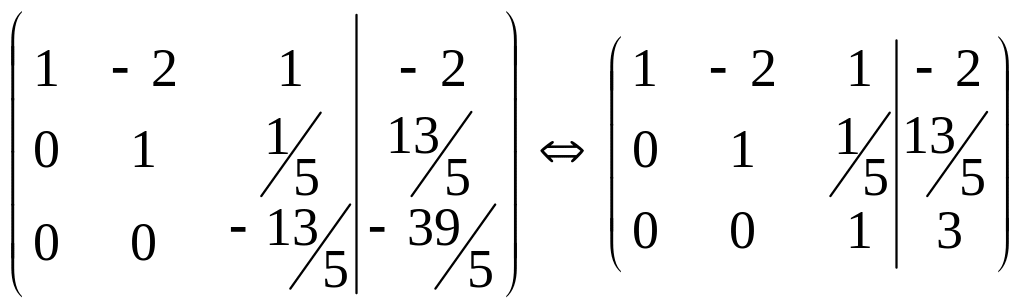 .
.
Відповідно запишемо систему:
![]()
З другого рівняння системи маємо:
![]() ,
,
а з першого рівняння:
![]() .
.
Отже, розв’язок системи
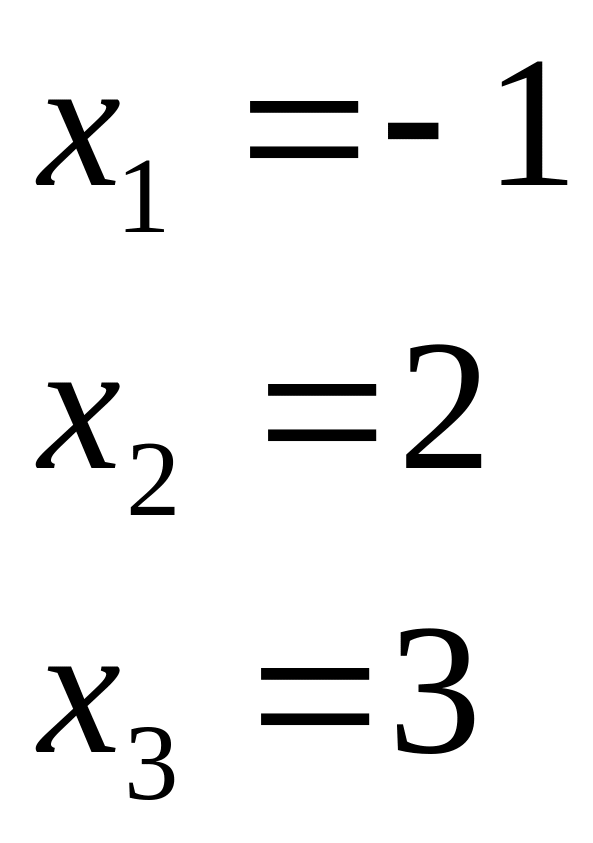 .
.
в) матричним методом
Розв’язання:
Систему
можна записати у матричному вигляді
![]() ,
де
,
де
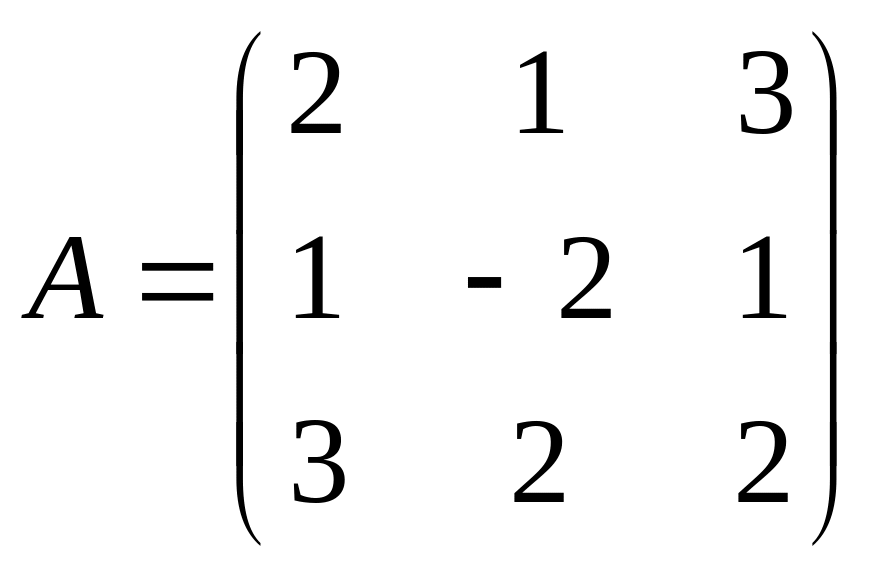 ,
,
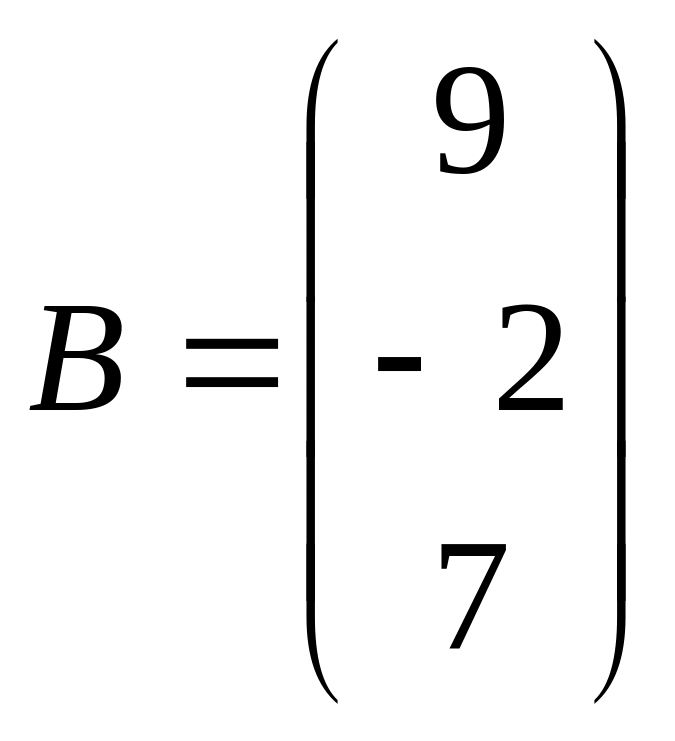 ,
,
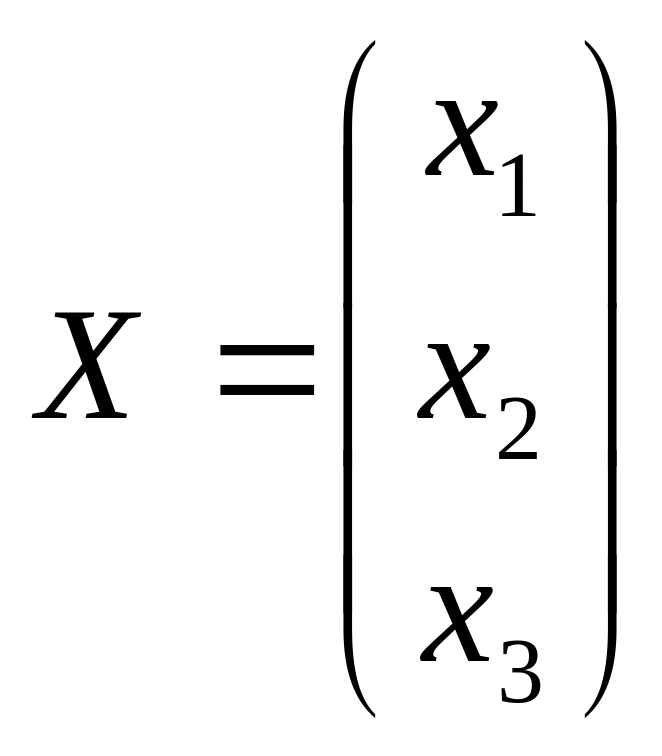 .
.
Тоді
(якщо
![]() )
розв’язок системи знаходимо за формулою
)
розв’язок системи знаходимо за формулою
![]() .
.
Знайдемо
матрицю
![]() ,
обернену до
,
обернену до
![]() .
.
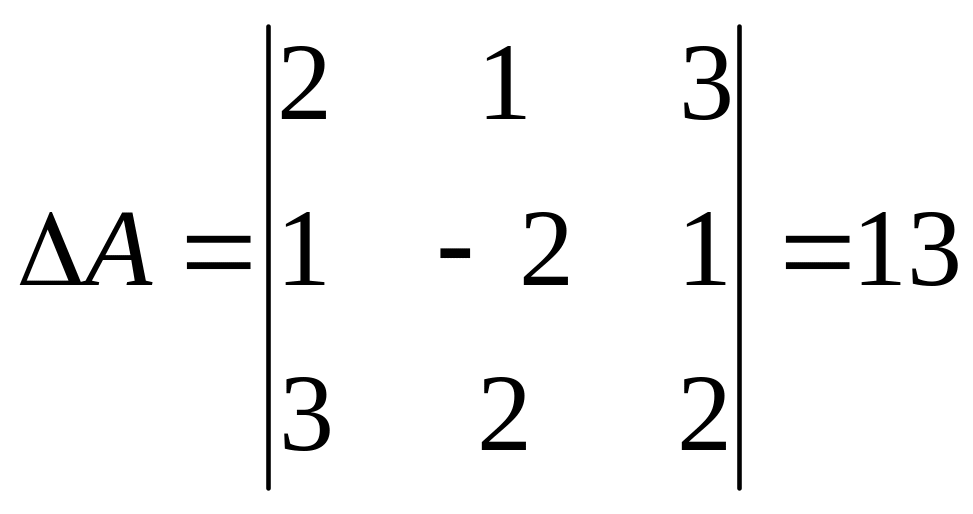 ,
,
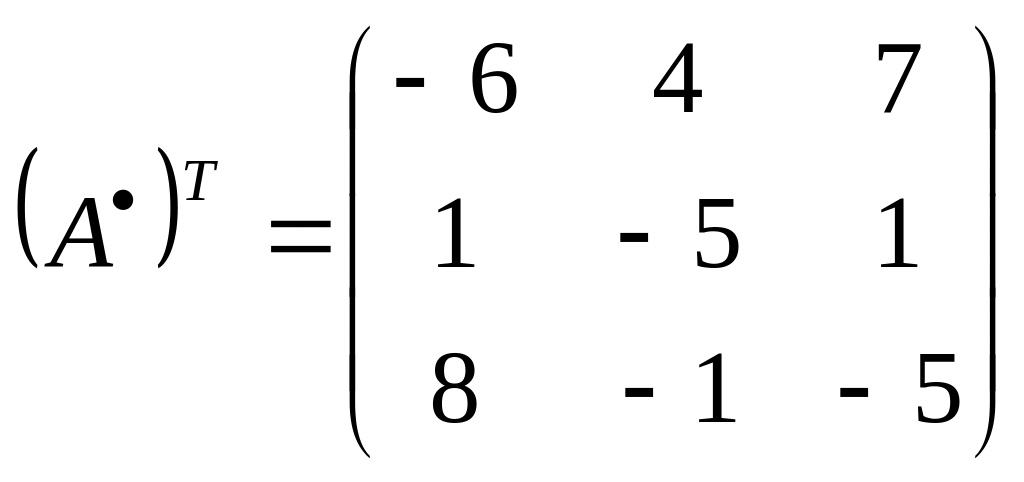 ,
,
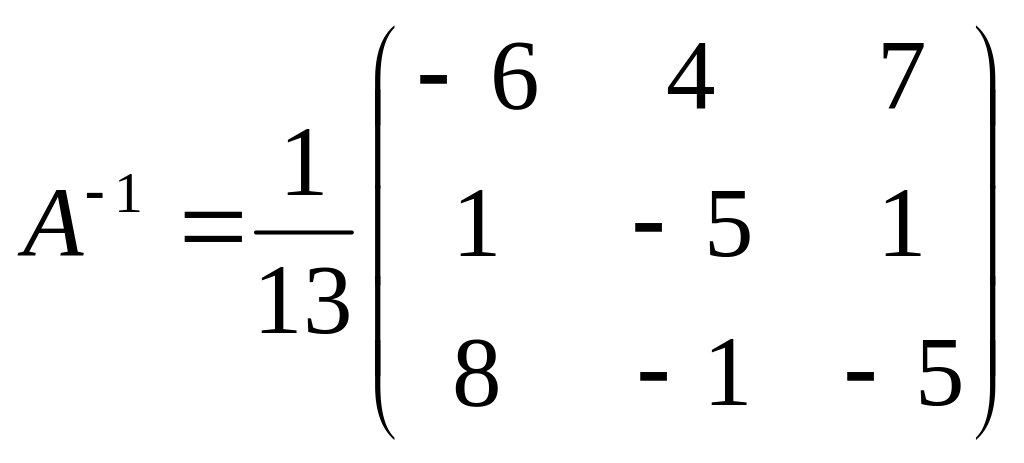 .
.
Тоді
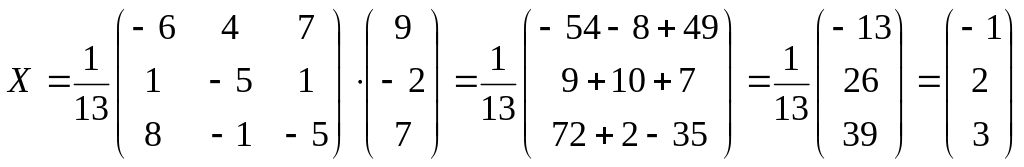 .
.
Таким чином, розв’язок системи
.
Приклад розв’язання завдання 2
а) Дано трикутник з вершинами А(1;1;1), В(5;1;-2) и С(7;9;1). Знайти координати точки D перетину бісектриси кута А зі стороною СВ.
Розв’язання:
Знаходимо довжини сторін трикутника АВС, що утворюють кут А:
![]() ,
,
![]() .
.
Так як бісектриса внутрішнього кута А ділить сторону СВ на частини, пропорційні довжинам прилеглих сторін, то
![]() .
.
Знаходимо:
![]()
![]()
![]()
Таким чином, D (17/3; 11/3; -1).
б) Скласти рівняння прямої, що утворює з додатним напрямом осі ОХ кут =60 і відтинає на осі ОУ відрізок, рівний 4.
Розв’язання:
За
формулою кутового коефіцієнта знаходимо
![]() .
.
Пряма відтинає на осі ординат відрізок, рівний 4, таким чином, її початкова ордината b=6.
Підставивши
знайдені значення k
і b в рівняння
прямої з кутовим коефіцієнтом, одержимо:
![]() або
або
![]()
в) Скласти канонічне рівняння еліпса, якщо фокусна відстань рівна 10, а мала вісь рівна 6.
Розв’язання:
Маємо
2с=10, тобто с=5, 2b=6,
тобто b=3,
![]() ,
звідки
,
звідки
![]() .
.
Відповідно,
![]() .
.
Приклад розв’язання завдання 3.
а)
Знайти
![]() .
.
Розв’язання: Границя знаменника дорівнює нулю .
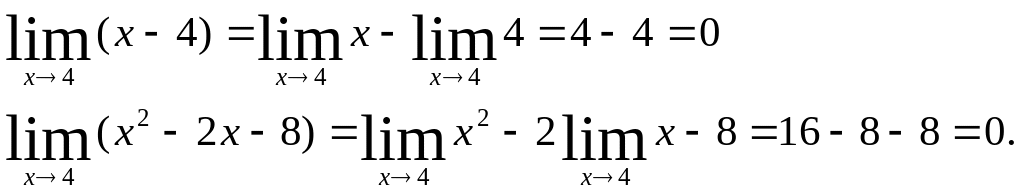
Отже,
теорему про границю частки застосовувати
не можна. Але поблизу точки
![]() ,
і тому дріб можна скоротити на х-4, тобто
,
і тому дріб можна скоротити на х-4, тобто
![]() .
.
Останній
вираз має зміст при всіх значеннях х,
тому
![]() .
У цьому випадку можна застосувати
теорему про границю суми:
.
У цьому випадку можна застосувати
теорему про границю суми:
![]() .
.
б)
Знайти
![]()
Розв’язання:
В
цьому випадку ні чисельник, ні знаменник
не мають границі, тому що обидва необмежено
зростають
![]() .
Але якщо попередньо перетворити
аналітичний вираз під знаком границі,
розділивши чисельник і знаменник на
х4,
то одержимо
.
Але якщо попередньо перетворити
аналітичний вираз під знаком границі,
розділивши чисельник і знаменник на
х4,
то одержимо
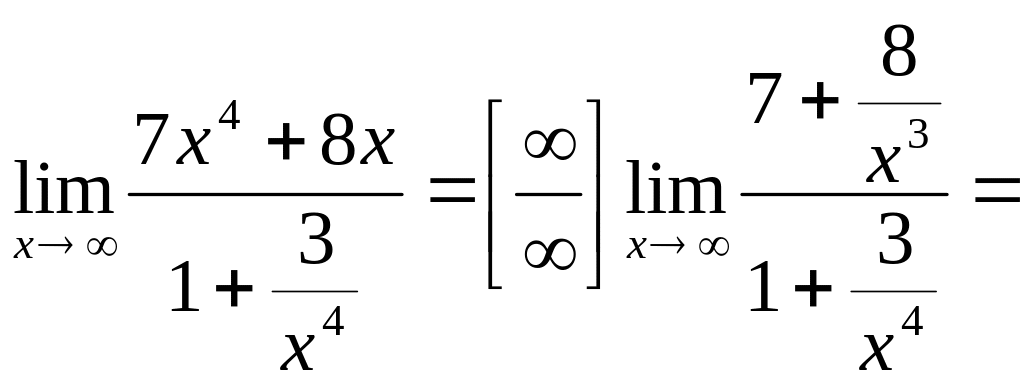
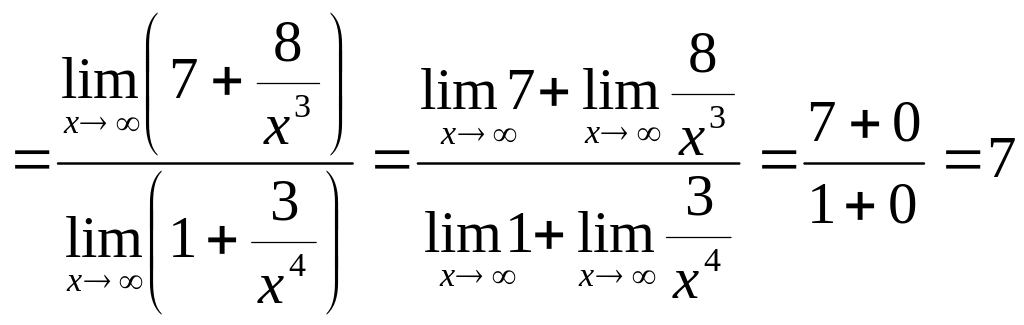
в) Знайти
![]()
Розв’язання: При безпосередній підстановці х=1 матимемо невизначеність . Це означає, що в чисельнику та знаменнику є множник (х-1), який їх перетворює в нуль.
Розділивши
чисельник на (х-1) за правилом ділення
многочленів, побачимо, що його можна
записати у вигляді
![]() .
Щоб виділити множник (х-1) у знаменнику,
множимо знаменник і чисельник на
спряжений йому вираз:
.
Щоб виділити множник (х-1) у знаменнику,
множимо знаменник і чисельник на
спряжений йому вираз:
![]()
![]()
![]()
![]()
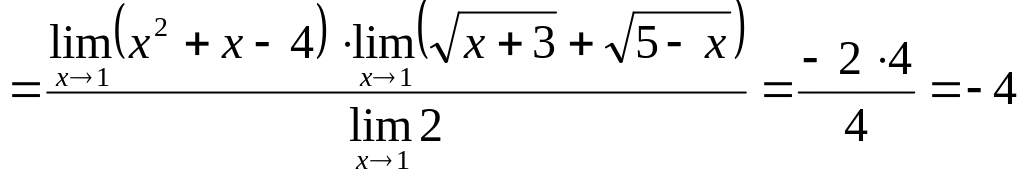
г) знайти
![]()
Розв’язання:
![]()
![]() ,
оскільки кожний із двох останніх
співмножників є границя типу
,
оскільки кожний із двох останніх
співмножників є границя типу
![]() ,
яка дорівнює одиниці.
,
яка дорівнює одиниці.
Приклад розв’язання завдання 4.
а) знайти
похідну функції
![]() .
.
Покладемо
![]() ,
де
,
де
![]() .
Тоді за правилом диференціювання
складної функції:
.
Тоді за правилом диференціювання
складної функції:
![]() .
.
б) Знайти
похідну функції
![]() .
.
Розв’язання:
Запишемо
функцію у вигляді
![]() .
.
Позначимо
![]() ,
тоді
,
тоді
![]() .
.
Маємо
![]()
![]()
![]() .
.
в) Знайти
похідну функції
![]() .
.
Розв’язання:
Запишемо
функцію у вигляді
![]() .
.
Маємо
![]() .
.
г) Знайти
похідну функції
![]() ,
,
![]() .
.
Маємо
![]()
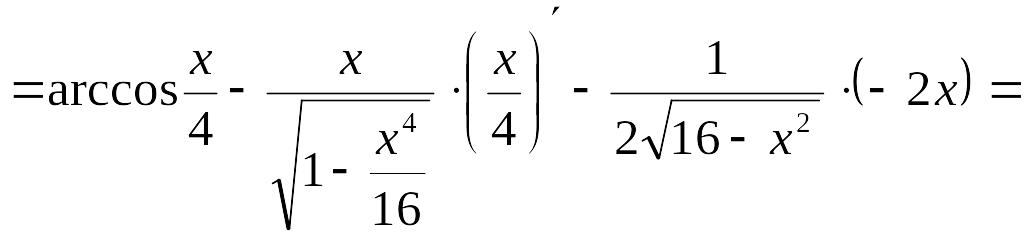
![]() ,
,
![]() .
.
Приклад розв’язання завдання 5.
Дослідити
функцію
![]() та побудувати її графік.
та побудувати її графік.
Розв’язання:
а) Область
визначення функції
![]() ,
тобто функція існує при всіх значеннях.
,
тобто функція існує при всіх значеннях.
б)
Парність, періодичність
![]() ,
,
![]() .
.
Функція загального вигляду, ні парна, ні непарна, неперіодична.
в) Точки перетину з осями координат:
з віссю ОХ:
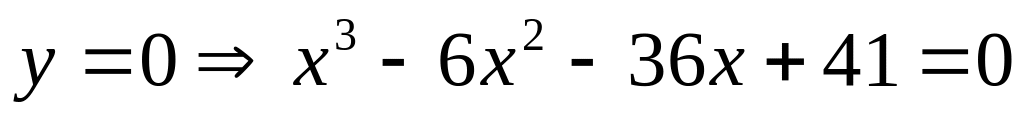 .
.
Легко
перевірити, що
![]() є корінь рівняння, тому
є корінь рівняння, тому
![]() .
.
Знайдемо
дві інші точки перетину графіка з віссю
ОХ:
![]()
![]() ,
,
![]() .
.
Точки перетину графіка з віссю ОХ – А(1;0), В(-4,37;0), С(9,37;0), точка перетину графіка з віссю OY (х=0) – D(0;41).
г) Інтервали зростання та спадання функції, точки екстремуму:
![]() ;
;
![]() .
.
Тоді
![]() - критичні точки.
- критичні точки.
Здобуті дані заносимо до таблиці.
x |
(-; -2) |
-2 |
(-2; 6) |
6 |
(6; +) |
f(x) |
+ |
0 |
- |
0 |
+ |
f(x) |
(зростає) |
81 |
(спадає) |
-175 |
(зростає) |
Точка максимуму функцій М (-2; 81), точка мінімуму N (6; -175).
д) Точка перетину, інтервали опуклості та вгнутості:
y=6x-12, y=0, 6x-12=0 x=2 – критична точка другого роду.
Дані заносимо до таблиці
x |
(-; 2) |
2 |
(6; +) |
f (x) |
- |
0 |
+ |
f(x) |
(опукла) |
-47 |
(вгнута) |
Точка перетину Е(2; -47).
е) Функція не має асимптот. Використовуючи здобуті данні, будуємо графік функції.