Вариант №11

Задание 1. Имеется идеальный газ, молярная теплоёмкость которого известна. Найти молярную теплоёмкость этого газа как функцию объёма, если газ совершает процесс по закону:

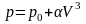
Задание 2. Найти уравнение процесса (в переменных T,V), при котором молярная теплоёмкость идеального газа изменяется по закону:

Задание 3. Идеальный газ совершает цикл, состоящий из: изобары, адиабаты и изотермы, причем процесс Т=Const происходит при минимальной температуре.

Задание 4. =4моль идеального газа сначала изобарически охладили, а затем изохорно расширили так, что температура газа стала равна первоначальной. Найти изменение энтропии газа, если его давление в данном процессе изменилось в n=4 раза.

Вариант №12

Задание 1. Имеется идеальный газ, молярная теплоёмкость которого известна. Найти молярную теплоёмкость этого газа как функцию объёма, если газ совершает процесс по закону:

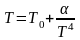
Задание 2. Найти уравнение процесса (в переменных T,V), при котором молярная теплоёмкость идеального газа изменяется по закону:

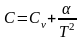
Задание 3. Идеальный газ совершает цикл, состоящий из:

изобары, адиабаты и изотермы, причем процесс Т=Const происходит при минимальной температуре.

Задание 4. Водород m=1г изобарически расширился в n=3раза и затем адиабатически сжали до первоначального объёма. Найти изменение энтропии в этом процессе.

Вариант №13

Задание 1. Имеется идеальный газ, молярная теплоёмкость которого известна. Найти молярную теплоёмкость этого газа как функцию объёма, если газ совершает процесс по закону:

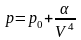
Задание 2. Найти уравнение процесса (в переменных T,V), при котором молярная теплоёмкость идеального газа изменяется по закону:

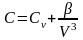
Задание 3. Идеальный газ совершает цикл, состоящий из: изохоры, адиабаты и изотермы, причем процесс Т=Const происходит при минимальной температуре.

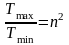
Задание 4. Найти приращение энтропии двух молей идеального газа с показателем адиабаты =1,30, если в результате некоторого процесса давление газа увеличилось в =2раза, а объём уменьшился в =3раза.

Вариант №14

Задание 1. Имеется идеальный газ, молярная теплоёмкость которого известна. Найти молярную теплоёмкость этого газа как функцию объёма, если газ совершает процесс по закону:

Задание 2. Найти уравнение процесса (в переменных T,V), при котором молярная теплоёмкость идеального газа изменяется по закону:

Задание 3. Идеальный газ совершает цикл, состоящий из: изобары, адиабаты и изотермы, причем процесс Т=Const происходит при максимальной температуре.

Задание 4. =2моля идеального газа с показателем адиабаты  совершает политропический процесс, в результате которого абсолютная температура газа увеличивается в 4 раза. Показатель политропы n. Найти приращение энтропии газа в этом процессе.

Вариант №15

Задание 1. Имеется идеальный газ, молярная теплоёмкость которого известна. Найти молярную теплоёмкость этого газа как функцию объёма, если газ совершает процесс по закону:

Задание 2. Найти уравнение процесса (в переменных T,V), при котором молярная теплоёмкость идеального газа изменяется по закону:

Задание 3. Идеальный газ совершает цикл, состоящий из: изохоры, адиабаты и изотермы, причем процесс Т=Const происходит при минимальной температуре.

Задание 4. При очень низких температурах теплоёмкость кристаллов , a,b=const. Найти энтропию кристалла как функцию температуры в этой области.