Приложение а
Образец выполнения задания 2
Решение системы линейных алгебраический уравнений (СЛАУ) методом Гаусса
Наиболее распространенным методом решения СЛАУ является метод последовательного исключения неизвестных (метод Гаусса).
Рассмотрим этот метод на примере системы четырех линейных уравнений с четырьмя неизвестными.
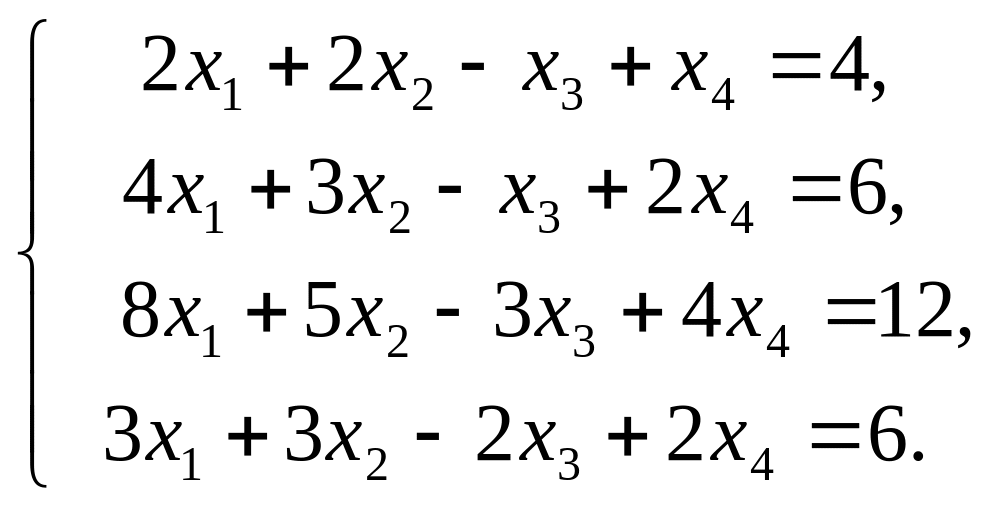
Решение
Составим расширенную матрицу системы и выполним прямой ход Гаусса путем сведения матрицы системы к треугольной матрице, с помощью элементарных преобразований матрицы
-
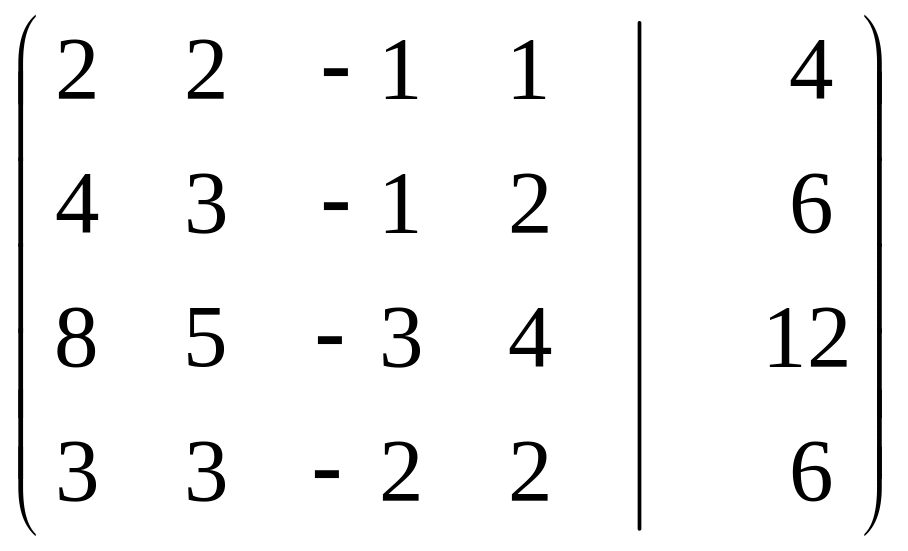
(1)
~
(2)
~
(2)
~
(3)-(5)
~
(6)
~
(6)
~
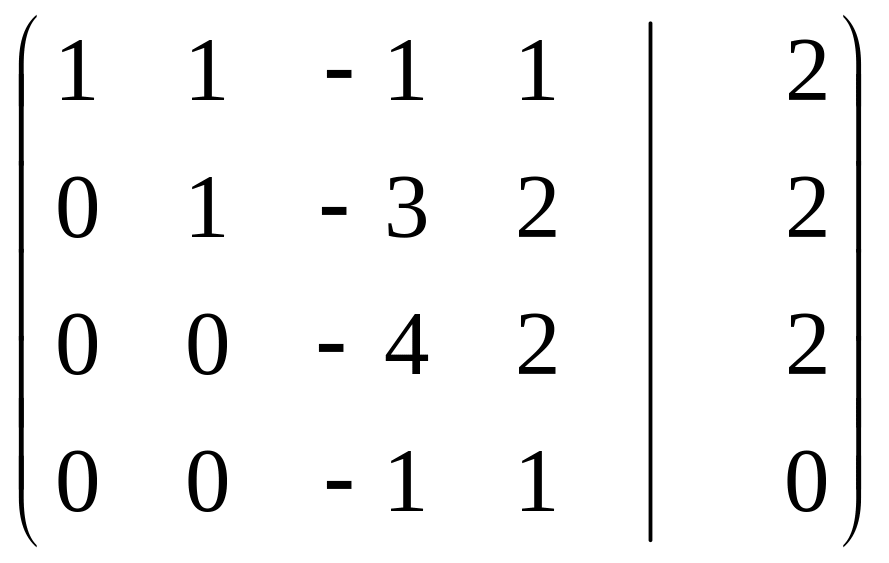
(7)
~
(8)
~
(8)
~
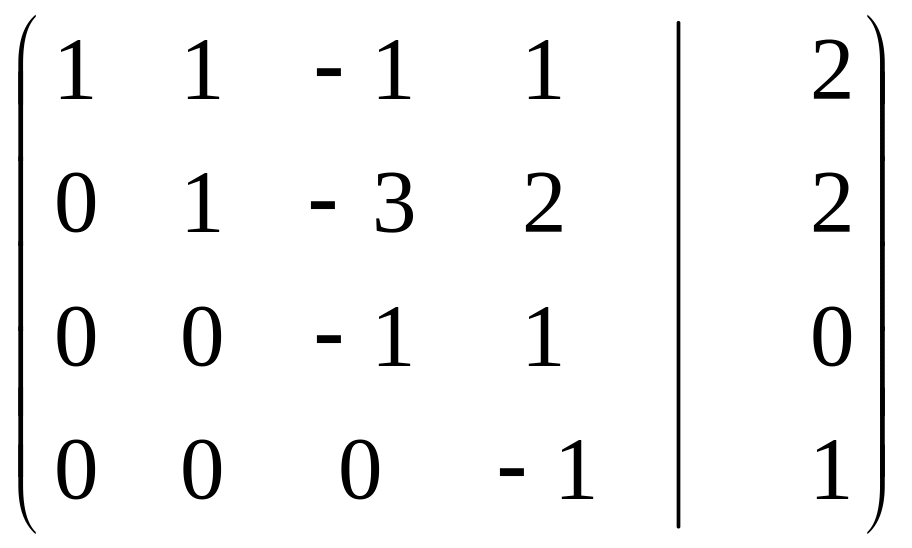
Приложение а
(продолжение)
Цифрами (1) – (8) указан порядок преобразования матрицы в эквивалентную.
1 Поменяем первую и четвертую строки расширенной матрицы системы местами.
2 Элементы четвертой строки умножим на (-1) и сложим с соответствующими элементами первой строки.
3 Элементы первой строки умножаем на (-4 ) и сложим с соответствующими элементами второй строки.
4 Элементы первой строки умножаем на (-8) и сложим с соответствующими элементами третьей строки.
5 Элементы первой строки умножаем на (-2) и сложим с соответствующими элементами четвертой строки.
6 Элементы второй строки умножаем на (-3) и сложим с соответствующими элементами третьей строки.
7 Поменяем третью и четвертую строки, поделив элементы третьей строки на 2.
8 Элементы третьей строки умножим на (-2) и сложим с соответствующими элементами четвертой строки.
Получили эквивалентную матрицу. Используя строки, полученной матрицы перейдем к системе
Выполним обратный ход Гаусса:
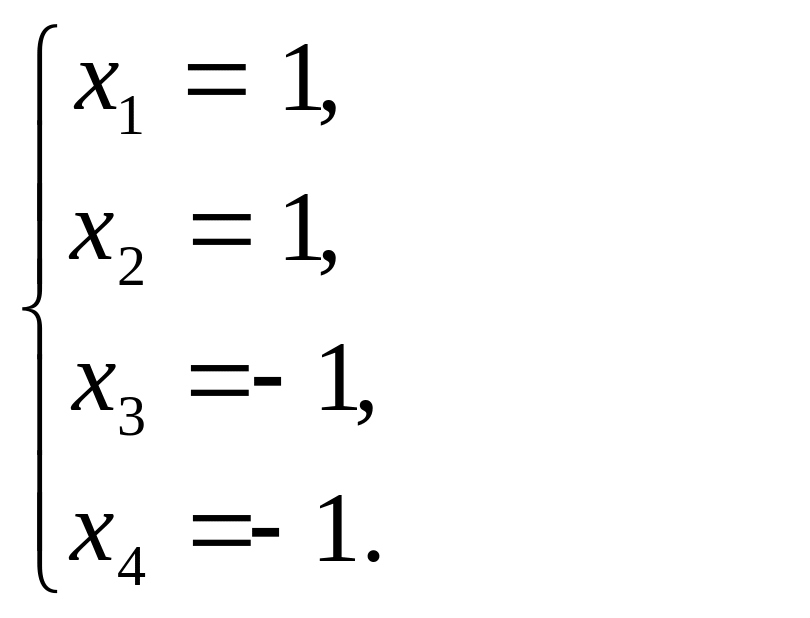
Ответ: (1; 1; -1; -1).
Замечание Подставляя найденные
в каждое из уравнений данной системы
можете выполнить проверку