Сечение цилиндра плоскостью.

При сечении цилиндра вращения плоскостью, параллельной оси вращения, в сечении получается пара прямых (образующих). Если секущая плоскость перпендикулярна к оси вращения, в сечении получается окружность. В общем случае, когда секущая плоскость наклонена к оси вращения цилиндра, в сечении получается эллипс.

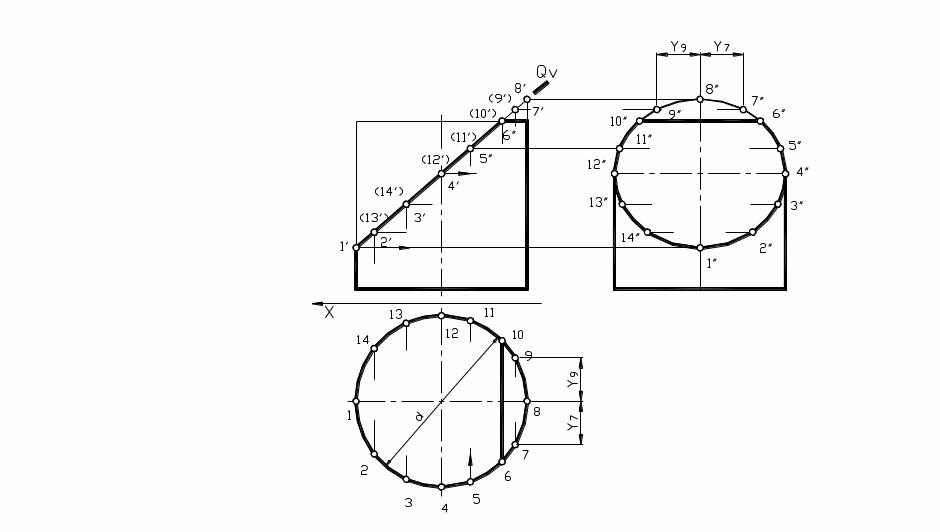
Рис. 38

На рисунке 38 показан пример построения проекций линии сечения цилиндра фронтально проецирующей плоскостью Q, когда в сечении получается эллипс.

Фронтальная проекция фигуры сечения в этом случае совпадает с фронтальным следом плоскости, а горизонтальная – с горизонтальной проекцией поверхности цилиндра – окружностью. Профильная проекция строится по двум имеющимся проекциям – горизонтальной и фронтальной.

Конус вращения – поверхность, образованная вращением прямой (образующая) вокруг пересекающейся с ней осью (направляющая).

Сечение конуса плоскостью

В зависимости от положения секущей плоскости в сечении конуса вращения могут получиться различные линии, называемые линиями конических сечений.

Если секущая плоскость проходит через вершину конуса, в его сечении получается пара прямых – образующих (треугольник). В результате пересечения конуса плоскостью, перпендикулярной к оси конуса, получается окружность. Если секущая плоскость наклонена к оси вращения конуса и не проходит через ее вершину, в сечении конуса могут получиться эллипс (секущая плоскость пересекает все образующие конуса); парабола (секущая плоскость параллельна одной из образующих конуса) или гипербола (в этом случае секущая плоскость параллельна двум образующим конуса) в зависимости от угла наклона секущей плоскости 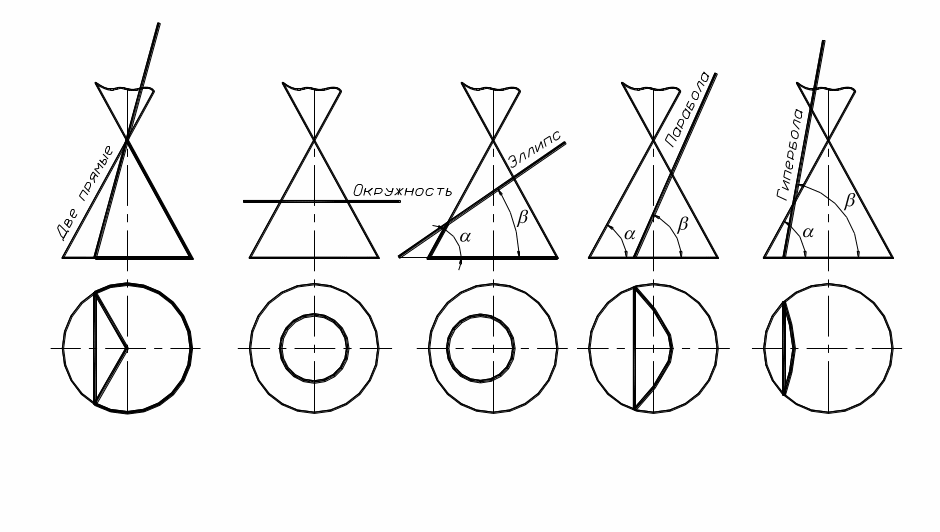(рис.39).

Рис. 39

Известно, что точка принадлежит поверхности, если она принадлежит какой-либо линии этой поверхности. Для конуса графически наиболее простыми линиями являются образующие и окружности. Следовательно, если по условию задачи требуется найти горизонтальные проекции точек, принадлежащих поверхности конуса, то нужно через точки провести одну из этих линий.

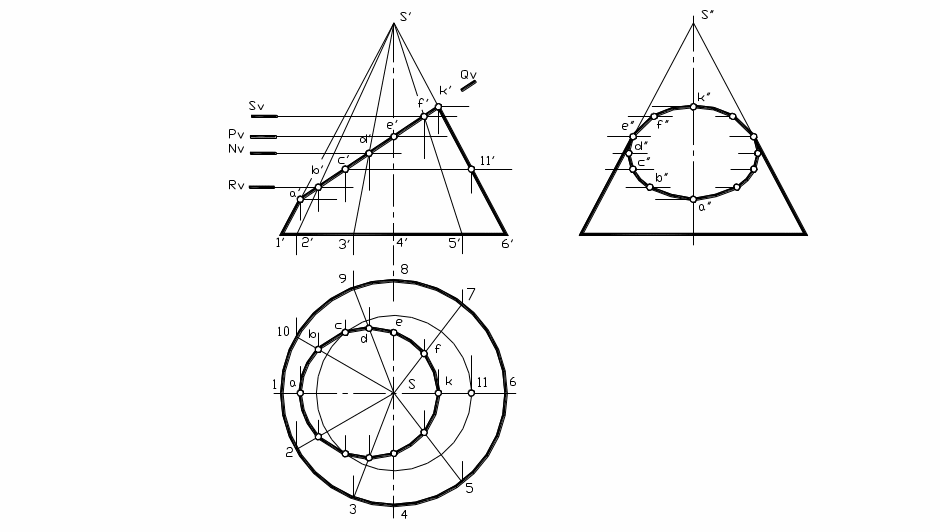
Рис.40

На рисунке 40 дан пример построения проекций линии сечения конуса фронтально проецирующей плоскостью, когда в сечении получается эллипс.

Для построения кривой линии, получаемой при пересечении конической поверхности плоскостью, в общем случае находят точки пересечения образующих конической поверхности с секущей плоскостью. Для этого можно поделить основание конуса на равное число частей (обычно 12), провести горизонтальные проекции образующих s1,s2,.... s12 и строят их фронтальные проекции. На фронтальной проекции отмечают фронтальные проекции точек пересечения построенных образующих с фронтальным следом секущей плоскости Q. Горизонтальные проекции строят в проекционной связи на соответствующих проекциях образующих. Профильная проекция линии сечения конуса плоскость Q построена по фронтальной и горизонтальной проекциям точек в проекционной связи.

Конус с вырезом.

На рисунке 41 показан конус, в котором выполнен вырез, образованный тремя плоскостями частного положения.

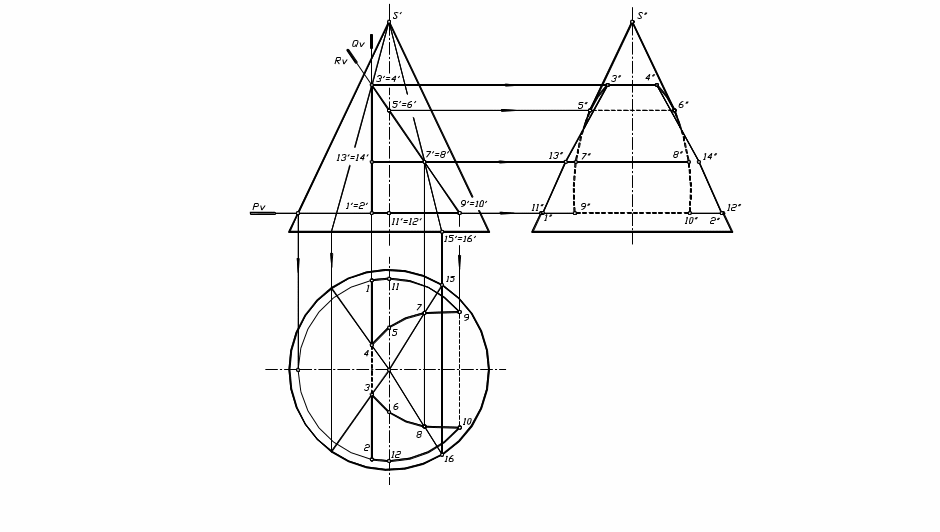
Рис. 41

При сечении конуса горизонтально проецирующей плоскостью Р в сечении образуется окружность соответствующего радиуса. Горизонтальные проекции точек 1,2,9,10,11,12 находятся на горизонтальной проекции этой окружности. Точки 11,12 принадлежат профильному очерку конуса. Линия выреза от этой плоскости в пределах выреза с одной сторону конуса – 1,11,9 и с другой – 2,12,10.

При сечении конуса фронтально проецирующей плоскость R в сечении образуется парабола. Точки 3,4,7,8 находятся путем проведения через них образующих конуса. Найдя на горизонтальной плоскости эти образующие, проецируем на них соответствующие точки. Профильные проекции этих точек находим по полученным фронтальным и горизонтальным. Соответственно линии сечения от этой плоскости в пределах выреза получаем с одной стороны конуса: 3,5,7,9 и с другой – 4,6,8,10.

При сечении конуса плоскостью профильного уровня Q в образуется гипербола. Конечные точки данной линии уже получены, для более точного построения можно взять еще пару промежуточных (13,14). Линия сечения от этой плоскости в пределах выреза 3,1 с одной стороны и 1,4 – с другой.

Полученные куски линии сечения шара с вырезом соединяем с учетом видимости. Принимая конус за сплошное тело, проводим на проекциях невидимые линии перегибов плоскостей, образующих вырез.

Примером поверхностей, образованных вращением окружности вокруг неподвижной оси является сфера.

Сфера – поверхность, полученная вращением окружности вокруг ее диаметра.