2.2. Построение дискриминантной функции

Таблица 14 «Построение дискриминантной функции»

Коэффициенты канонической дискриминантрой функции
	Функция
	1
x1	,000013
x2	,00064
x3	,0018
x4	-,011
x5	,0000002
(Константа)	-2,076
Ненормированные коэффициенты

Исходя из Таблицы 14 дискриминантная функция, построенная с помощью метода включения всех переменных, имеет вид:

d=-2,076+0,000013x₁+0,00064x₂+0,0018x₃-0,011x₄+0,0000002x₅

Таблица 15 «Средние значения дискриминантной функции в обоих кластерах»

Функции в центроидах групп
Кластерный номер наблюдения	Функция
	1
1	2,846
2	-1,067
Ненормированные канонические дискриминантные функции вычислены в центроидах групп.

Исходя из Таблицы 15, константа = =0,8895

Рассмотрим новые наблюдения:

1) г.Москва: =-2,076+0,000013*17141+0,00064*14493+0,0018*71-0,011*110,1+0,0000002*194820213=45,30; > → г.Москва относится к первому кластеру – наиболее развитым регионам России.

2) Нижегородская область: =-2,076+0,000013*6340+0,00064*10946+0,0018*109-0,011*112,3+0,0000002* 24697350=8,91; > → Нижегородская область относится к первому кластеру – наиболее развитым регионам России.

3) Сахалинская область: =-2,076+0,000013*1617+0,00064*708+0,0018*3-0,011*104,8+0,0000002*708084=-2,61; < → Сахалинская область относится ко второму кластеру – регионам России с более низким уровнем экономического развития.

2.3. Графический анализ результатов классификации

На Рисунке 8 представлено распределение объектов на кластеры после уточнения результатов классификации с помощью аппарата дискриминантного анализа. Кластер 2 по-прежнему имеет кластерное облако эллипсоидной формы, а облако кластера 1 стало более вытянутым и по форме больше напоминает эллипс.

Распределение значения дискриминантной функции отдельно по группам изображается на двух отдельных гистограммах (Рисунки 9 и 10). Кластер 1 более однороден по сравнению со вторым. Можно заметить, что значения дискриминантной функции для обеих групп немного смещены вправо относительно среднего значения.

Рисунок 8 «Классификация регионов России в осях первой и второй главных компонент после уточнения результатов классификации»

Рисунок 9 «Распределение значений дискриминантной функции для кластера 1»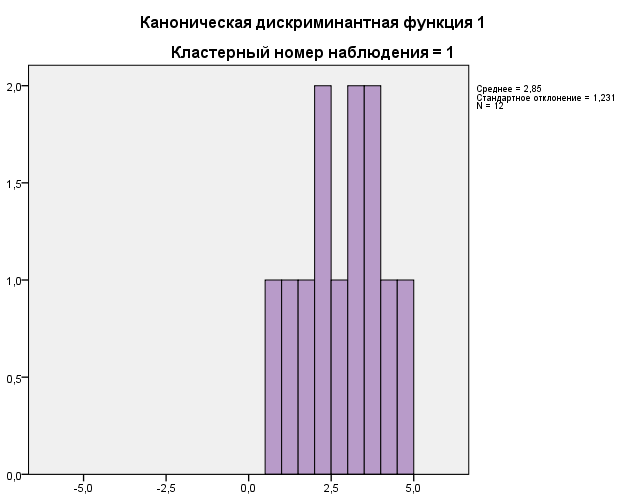

Рисунок 10 «Распределение значений дискриминантной функции для кластера 2»

§3. «Построение дискриминантной функции с помощью пошагового алгоритма»

Таблица 16 «Переменные в анализе»

Переменные в анализе
Шаг		Толерантность	F исключения	Мин. D квадрат	Между группами
1	x2	1,000	103,163
2	x2	,998	59,833	2,967	1 и 2
	x5	,998	6,161	11,821	1 и 2

Как видно из Таблицы 16, в анализ по очереди будут включены переменные: число зарегистрированных преступлений в сфере экономики (x₂), объем внутренних затрат на научные исследования и разработки (x₅).

Таблица 17 «Построение дискриминантной функции»

Коэффициенты канонической дискриминантрой функции
	Функция
	1
x2	,00074
x5	0,0000002
(Константа)	-3,090
Ненормированные коэффициенты

Исходя из Таблицы 17 дискриминантная функция, построенная с помощью пошагового алгоритма дискриминантного анализа, имеет вид:

d=-3,090+0,00074x₂+0,0000002x₅

Таблица 18 «Средние значения дискриминантной функции в обоих кластерах»

Функции в центроидах групп
Кластерный номер наблюдения	Функция
	1
1	2,752
2	-1,032
Ненормированные канонические дискриминантные функции вычислены в центроидах групп.

Исходя из Таблицы 18, константа = =0,86

Рассмотрим новые наблюдения:

1) г.Москва: =-3,090+0,00074*14493+0,0000002*194820213=46,60; > → г.Москва относится к первому кластеру – наиболее развитым регионам России.

2) Нижегородская область: =-3,090+0,00074*10946+0,0000002*24697350=9,95; > → Нижегородская область относится к первому кластеру – наиболее развитым регионам России.

3) Сахалинская область: =-3,090+0,00074*708+0,0000002*708084=-2,42; < → Сахалинская область относится ко второму кластеру – регионам России с более низким уровнем экономического развития.

Результаты аналогичны тем, которые мы получили при помощи дискриминантной функции, построенной методом включения всех переменных.