
- •Индивидуальная работа №1. Тема. Предел функции. Непрерывность функции
- •Индивидуальная работа №2. Тема. Производная и дифференциал функции
- •Индивидуальная работа №3. Тема. Применение дифференциального исчисления для исследования функций
- •Индивидуальная работа №4. Тема. Применение дифференциального исчисления в экономических исследованиях
- •Индивидуальная работа №5. Тема. Экстремумы функций многих переменных
- •Индивидуальная работа №6. Тема. Методы интегрирования. Определенный интеграл
- •Индивидуальная работа №7. Тема. Числовые ряды
ФЕДЕРАЛЬНОЕ АГЕНТСТВО ПО ОБРАЗОВАНИЮ
ГОСУДАРСТВЕННОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ ВЫСШЕГО ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ
«КАЗАНСКИЙ ГОСУДАРСТВЕННЫЙ ФИНАНСОВО- ЭКОНОМИЧЕСКИЙ ИНСТИТУТ»
Кафедра математики и экономической информатики
Методическая разработка
по дисциплине «Математика»
для организации индивидуальной работы студентов,
обучающихся по направлению 080100.62 «Экономика»
(I семестр)
Казань 2009
Обсуждена на заседании кафедры математики и экономической информатики 27.12.08, протокол №5
Составители: к.ф.-м.н, профессор Марданов Р.Ш.,
к.ф.-м.н., доцент Хасанова А.Ю.
Рецензент: к.ф.-м.н., доцент Султанов Р.А.
Введение
План-график организации учебного процесса по математике на ОЭФ предусматривает индивидуальные занятия в течение первых трех семестров по 14 часов в каждом семестре.
В соответствии с программой курса «Математика» и календарно-тематическим планом студенты 1 курса ОЭФ в первом семестре изучают часть I – «Математический анализ и элементы аналитической геометрии». Согласно календарно-тематическому плану студенты должны выполнить 7 индивидуальных работ. Индивидуальные работы включают следующие темы:
– Предел функции. Непрерывность функции;
– Производная и дифференциал функции;
– Применение дифференциального исчисления для исследования функций;
– Применение дифференциального исчисления в экономических исследованиях;
– Экстремумы функции двух переменных;
– Методы интегрирования. Определенный интеграл;
– Числовые ряды.
По каждой теме приводятся 30 вариантов заданий. В рамках индивидуальных занятий по математике студенты должны выполнить по одному варианту задания соответствующей темы. На выполнение одного варианта индивидуальных заданий по каждой теме отводится 2 часа. Контроль знаний осуществляется путем проверки письменной работы и оценки по балльно-рейтинговой системе.
Индивидуальная работа №1. Тема. Предел функции. Непрерывность функции
Найти пределы (а, б, в). Провести неполное исследование и построить эскиз графика функции (г).
1. а)
![]() ; б)
; б)
![]() ;
;
в)
![]() ; г)
; г)
![]() .
.
2. а)
![]() ;
б)
;
б)
![]() ;
;
в)
![]() ; г)
; г)
![]() .
.
3. а)
![]() ; б)
; б)
![]() ;
;
в)
![]() ; г)
; г)
![]() .
.
4. а)
![]() ; б)
; б)
![]() ;
;
в)
![]() ; г)
; г)
![]() .
.
5. а)
![]() ; б)
; б)
![]() ;
;
в)
![]() ; г)
; г)
![]() .
.
6. а)
 ; б)
; б)
![]() ;
;
в)
![]() ; г)
; г)
![]() .
.
7. а)
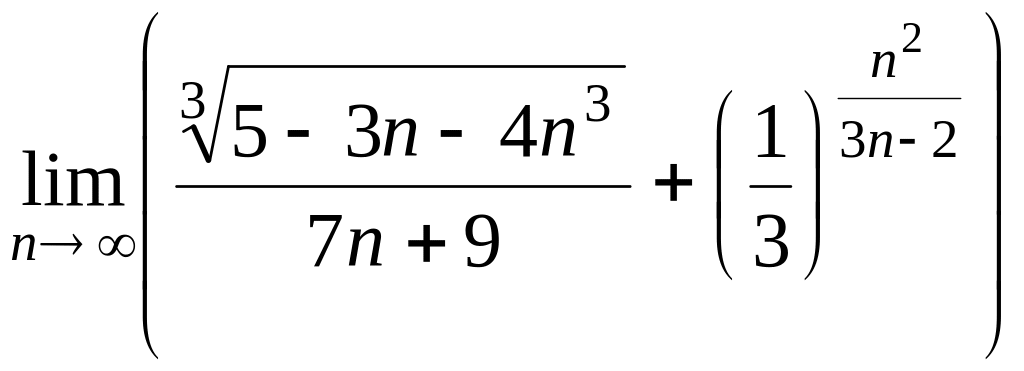 ; б)
; б)
![]() ;
;
в)
![]() ; г)
; г)
![]() .
.
8. а)
![]() ; б)
; б)
![]() ;
;
в)
![]() ; г)
; г)
![]() .
.
9. а)
![]() ; б)
; б)
![]() ;
;
в)
![]() ; г)
; г)
![]() .
.
10. а)
![]() ; б)
; б)
![]() ;
;
в)
![]() ; г)
; г)
![]() .
.
11. а)
![]() ; б)
; б)
![]() ;
;
в)
![]() ; г)
; г)
![]() .
.
12. а)
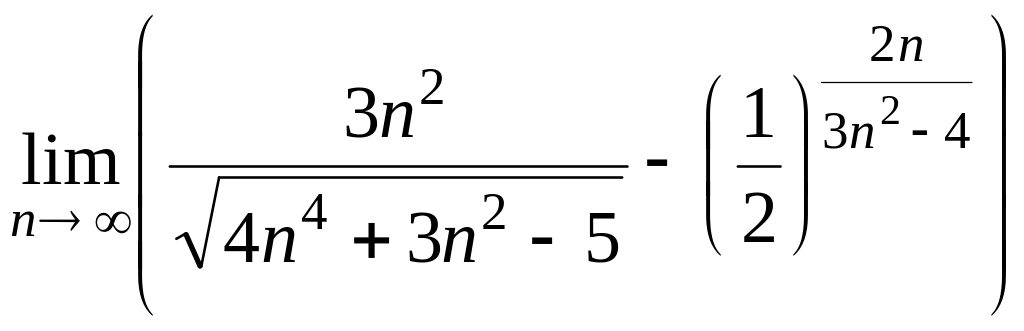 ; б)
; б)
![]() ;
;
в)
![]() ; г)
; г)
![]() .
.
13. а)
![]() ; б)
; б)
![]() ;
;
в)
![]() ; г)
; г)
![]() .
.
14. а)
![]() ; б)
; б)
![]() ;
;
в)
![]() ; г)
; г)
![]() .
.
15. а)
![]() ; б)
; б)
![]() ;
;
в)
![]() ; г)
; г)
![]() .
.
16. а)
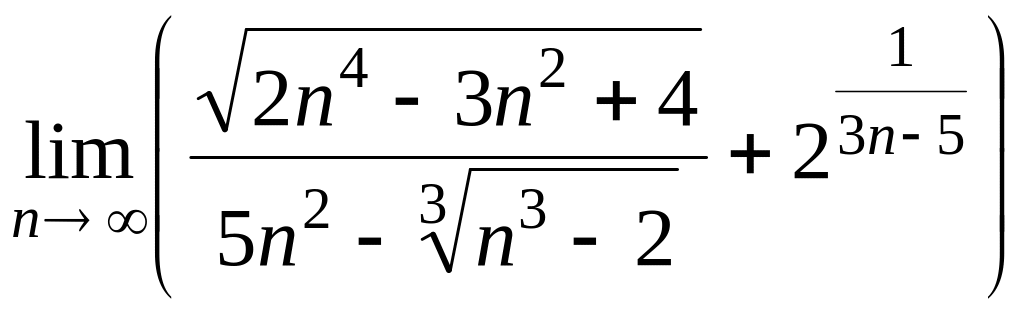 ; б)
; б)
![]() ;
;
в)
![]() ; г)
; г)
![]() .
.
17. а)
![]() ; б)
; б)
![]() ;
;
в)
![]() ; г)
; г)
![]() .
.
18. а)
![]() ; б)
; б)
![]() ;
;
в)
![]() ; г)
; г)
![]() .
.
19. а)
![]() ; б)
; б)
![]() ;
;
в)
![]() ; г)
; г)
![]() .
.
20. а)
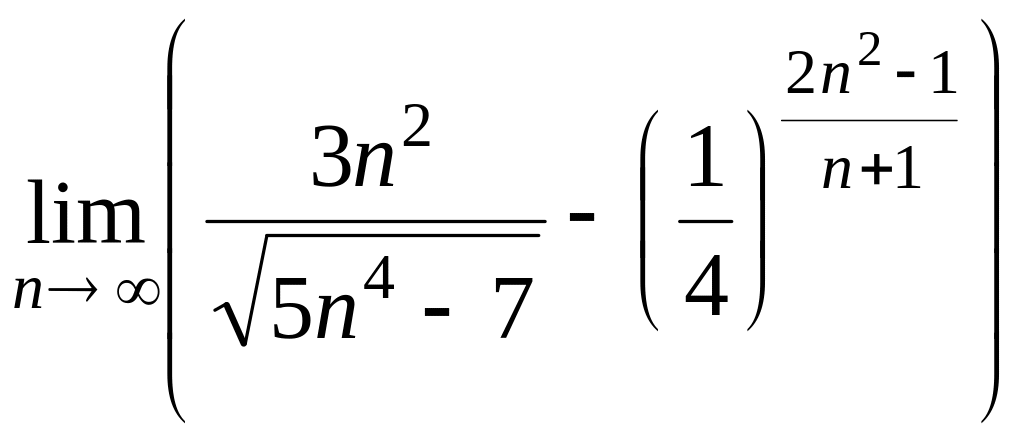 ; б)
; б)
![]() ;
;
в)
![]() ; г)
; г)
![]() .
.
21. а)
![]() ; б)
; б)
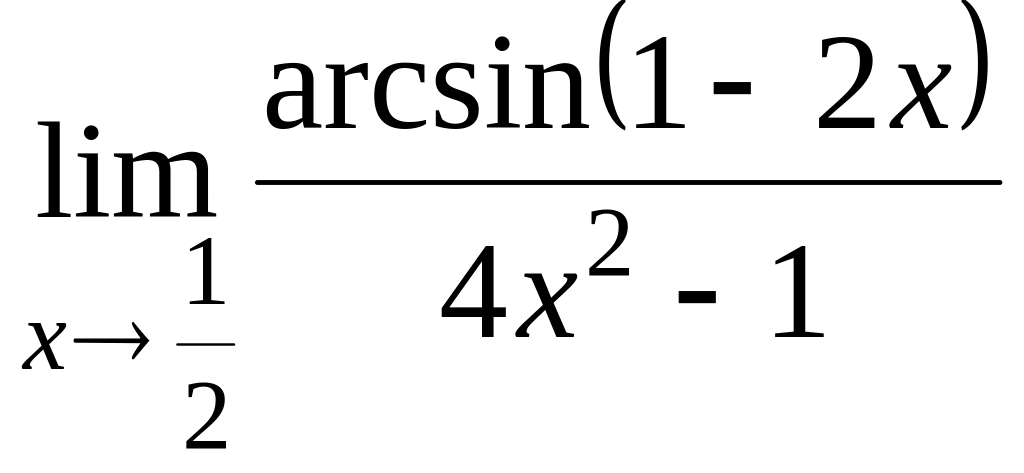 ;
;
в)
![]() ; г)
; г)
![]() .
.
22. а)
![]() ; б)
; б)
![]() ;
;
в)
![]() ; г)
; г)
![]() .
.
23. а)
![]() ; б)
; б)
![]() ;
;
в)
![]() ; г)
; г)
![]() .
.
24. а)
![]() ; б)
; б)
![]() ;
;
в)
![]() ; г)
; г)
![]() .
.
25. а)
 ; б)
; б)
![]() ;
;
в)
![]() ; г)
; г)
![]() .
.
26. а)
![]() ; б)
; б)
![]() ;
;
в)
![]() ; г)
; г)
![]() .
.
27. а)
![]() ; б)
; б)
![]() ;
;
в)
![]() ; г)
; г)
![]() .
.
28. а)
![]() ; б)
; б)
![]() ;
;
в)
![]() ; г)
; г)
![]() .
.
29) а)
![]() ; б)
; б)
 ;
;
в)
![]() ; г)
; г)
![]() .
.
30. а)
![]() ; б)
; б)
![]() ;
;
в)
![]() ; г)
; г)
![]() .
.
Индивидуальная работа №2. Тема. Производная и дифференциал функции
Найти:
– производную функции (а);
– дифференциал функции (б);
– производную неявной функции (в);
– используя правило Лопиталя, вычислить пределы функций (г, д).
1. а)
![]() ; б)
; б)
![]() ;
;
в)
![]() ;
г)
;
г)
![]() ;
д)
;
д)
 .
.
2. а)
![]() ; б)
; б)
![]() ;
;
в)
![]() ;
г)
;
г)
![]() ;
д)
;
д)
![]() .
.
3. а)
![]() ; б)
; б)
![]() ;
;
в)
![]() ;
г)
;
г)
![]() ;
д)
;
д)
![]() .
.
4. а)
![]() ; б)
; б)
![]() ;
;
в)
![]() ;
г)
;
г)
![]() ;
д)
;
д)
![]() .
.
5. а)
![]() ; б)
; б)
![]() ;
;
в)
![]() ;
г)
;
г)
![]() ;
д)
;
д)
![]() .
.
6. а)
![]() ; б)
; б)
![]() ;
;
в)
![]() ;
г)
;
г)
![]() ;
д)
;
д)
![]() .
.
7. а)
![]() ; б)
; б)
![]() ;
;
в)
![]() ;
г)
;
г)
![]() ;
д)
;
д)
![]() .
.
8. а)
![]() ; б)
; б)
![]() ;
;
в)
![]() ;
г)
;
г)
![]() ;
д)
;
д)
![]() .
.
9. а)
![]() ; б)
; б)
![]() ;
;
в)![]() ;
г)
;
г)![]() ;
д)
;
д)
![]() .
.
10. а)
![]() ; б)
; б)
![]() ;
;
в)
![]() ;
г)
;
г)
![]() ;
д)
;
д)
![]() .
.
11. а)
![]() ; б)
; б)
![]() ;
;
в)
![]() ;
г)
;
г)
![]() ;
д)
;
д)
![]() .
.
12. а)
![]() ; б)
; б)
![]() ;
;
в)
![]() ;
г)
;
г)
![]() ;
д)
;
д)
![]() .
.
13. а)
![]() ; б)
; б)
![]() ;
;
в)
![]() ;
г)
;
г)
![]() ;
д)
;
д)
![]() .
.
14. а)
![]() ; б)
; б)
![]() ;
;
в)
![]() ;
г)
;
г)
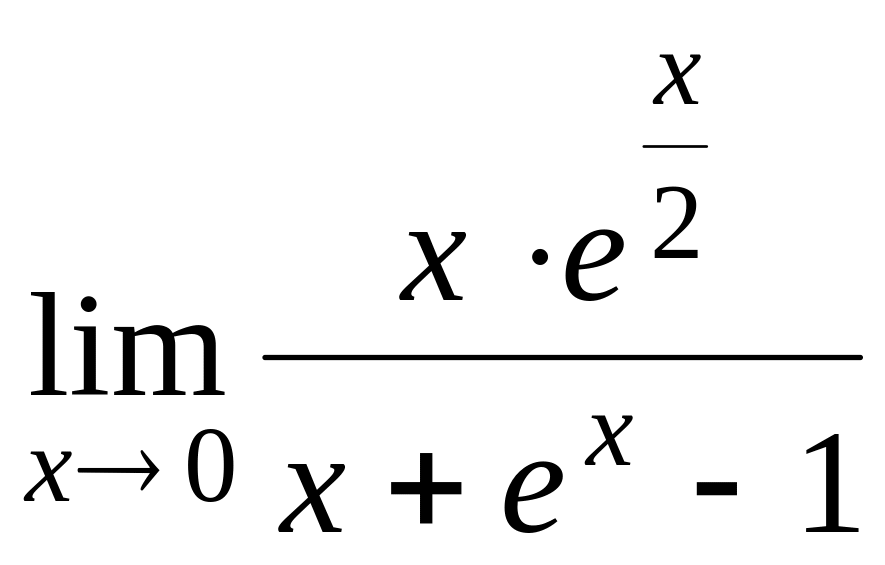 ;
д)
;
д)
![]() .
.
15. а)
![]() ; б)
; б)
![]() ;
;
в)
![]() ;
г)
;
г)
 ;
д)
;
д)
![]() .
.
16. а)
![]() ; б)
; б)
![]() ;
;
в)
![]() ;
г)
;
г)
![]() ;
д)
;
д)
![]() .
.
17. а)
![]() ; б)
; б)
![]() ;
;
в)
![]() ;
г)
;
г)
![]() ;
д)
;
д)
![]() .
.
18. а)
![]() ; б)
; б)
![]() ;
;
в)
![]() ;
г)
;
г)
![]() ;
д)
;
д)
![]() .
.
19. а)
![]() ; б)
; б)
![]() ;
;
в)
![]() ;
г)
;
г)
![]() ;
д)
;
д)
![]() .
.
20. а)
![]() ; б)
; б)
![]() ;
;
в)
![]() ;
г)
;
г)
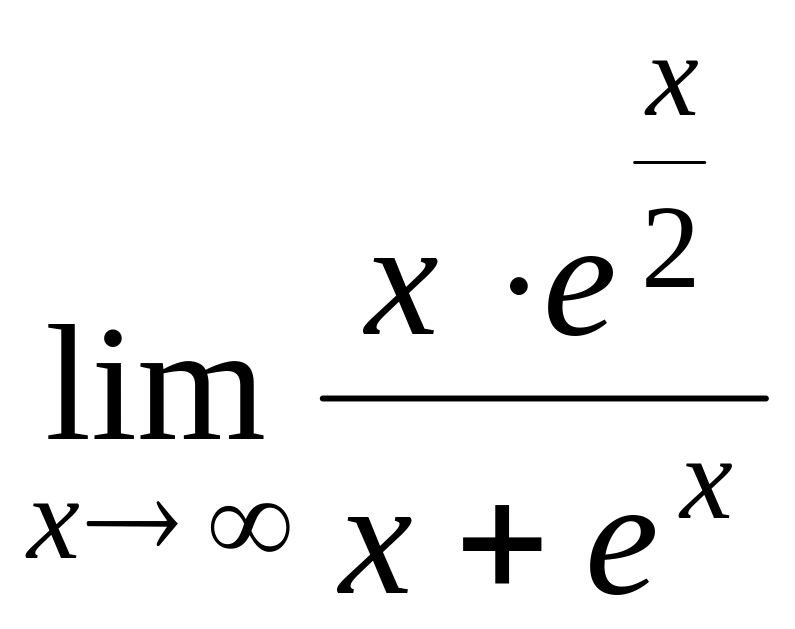 ;
д)
;
д)
![]() .
.
21. а)
![]() ; б)
; б)
![]() ;
;
в)
![]() ;
г)
;
г)
![]() ;
д)
;
д)
![]() .
.
22. а)
![]() ; б)
; б)
![]() ;
;
в)
![]() ;
г)
;
г)
![]() ;
д)
;
д)
![]() .
.
23. а)
![]() ; б)
; б)
![]() ;
;
в)
![]() ;
г)
;
г)
![]() ;
д)
;
д)
![]() .
.
24. а)
![]() ; б)
; б)
![]() ;
;
в)
![]() ;
г)
;
г)
![]() ;
д)
;
д)
![]() .
.
25. а)
![]() ; б)
; б)
![]() ;
;
в)
![]() ;
г)
;
г)
![]() ;
д)
;
д)
![]() .
.
26. а)
![]() ; б)
; б)
![]() ;
;
в)
![]() ;
г)
;
г)
![]() ;
д)
;
д)
![]() .
.
27. а)
![]() ; б)
; б)
![]() ;
;
в)
![]() ;
г)
;
г)
![]() ;
д)
;
д)
![]() .
.
28. а)
![]() ; б)
; б)
![]() ;
;
в)
![]() ;
г)
;
г)
![]() ;
д)
;
д)
![]() .
.
29. а)
![]() ; б)
; б)
![]() ;
;
в)![]() ;
г)
;
г)![]() ;
д)
;
д)
![]() .
.
30. а)
![]() ; б)
; б)
![]() ;
;
в)
![]() ;
г)
;
г)
![]() ;
д)
;
д)
 .
.
