Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Оренбургский Государственный Университет

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

Отчет по лабораторной работе №7 по ТОУ 4 курc.doc

Скачиваний:

Добавлен:

14.11.2019

Размер:

686.59 Кб

Скачать

☆

1 / 21 2 > Следующая >>>

Министерство образования Российской Федерации

Государственное образовательное учреждение

Высшего профессионального образования

«ОРЕНБУРГСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ»

Математический факультет

Кафедра Прикладной математики

ОТЧЕТ

По лабораторной работе №7

по курсу Теория оптимального управления

Метод динамического программирования для дискретной задачи оптимального управления

ОГУ 010200.6006.02 О

Руководитель

_____________ Иванова Ю.П.

“___ ”______________2011 г.

Исполнитель

студент гр. 08 ПриМ

_______________Кияева Е. А.

“___ ” _____________2011 г.

Оренбург 2011

Содержание

Постановка задачи………………………………………………………..3

Алгоритм реализации схемы Беллмана….…………….………….……7

Практическая часть……………………………………………………….8

Приложение А – Код программы…….……………………………….11

Постановка задачи

Рассмотрим модель очистки воды от загрязнения органическими отходами.

Задача оптимального управления с ограничениями на управление:

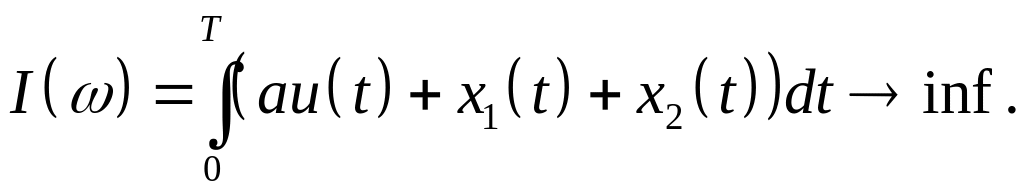(1)

(2)

(3)

(4)

(5)

(6)

Здесь (мг. /ед.врем. л) – количество отходов, удаленных из единицы объема в единицу времени;

(мг. /л) – концентрация органических отходов в момент времени t;

( мг. /л.) – дефицит кислорода в воде в момент времени t;

а (ед.врем.) – коэффициент, характеризующий стоимость работ в единицу времени;

(1/ ед.врем.) – коэффициент отбора кислорода за единицу времени;

(1/ед.врем.) – коэффициент реаэрации в единицу времени;

– начальное значение в момент дефицита кислорода и концентрации отходов соответственно;

В уравнении (2) производная (мг. /ед.врем. л) характеризует скорость разложения отходов в единицу времени.

В уравнении (3) (мг. /ед.врем. л) характеризует динамику дефицита кислорода в единицу времени.

В неравенстве (мг. /ед.врем. л) – максимальное количество отходов, удаленных из единицы объема в единицу времени.

Целью управления является минимизация суммарных затрат на проведение очистных работ, уменьшение концентрации отходов и дефицита кислорода в течении рассматриваемого периода времени Т.

Провести эксперимент при следующих значениях параметров и программно реализовать его:

Применим для решения задачи (1) – (6) схему Беллмана. Для определенности будем считать, что в задаче и заданы параллельные фазовые ограничения.

Алгоритм реализации схемы Беллмана

Шаг	Действие
0	Задать разбиения: а) отрезка времени : б) – ограничения по в) – ограничения по г) – ограничения по u ;
Первый этап (по убывающему индексу)
1	Вычислить значения функции Беллмана в точках терминального множества , где
2	Начало цикла по ;
3	Положить – число проколотых точек. (Точка называется проколотой, если она не принадлежит множеству достижимости) Организовать цикл по точкам множества ;
4	Вычислить координаты точки
5	Положить – число недопустимых управлений в точке ;
6	Организовать цикл по допустимым управлениям ;
7	Вычислить управления ;
8	Вычислить точку ;
9	Проверить выполнение фазового ограничения (принадлежит ли точка множеству ):
10	Найти ближайшую к непроколотую точку сетки ; если все ближайшие точки сетки (т.е. точки, находящиеся на расстоянии меньше чем ) являются проколотыми, то и переход к шагу 14;
11	Вычислить ;
12	Найти ;
13	Положить ;
14	Перейти к следующему шагу цикла по n, т.е. положить и проверить условие окончания цикла: ;
15	Проверяем, не является ли точка проколотой:
16	Перейти к следующей итерации цикла по i,j, т.е. а) положить и проверить условие б) положить и проверить условие
17	Проверить, все ли точки сетки являются непроколотыми:
18	Перейти к следующей итерации цикла по , т.е. полагаем и проверить условие окончания цикла:
19	Получить функцию Беллмана и − синтез управления;
Второй этап
20	Найти ближайшую к непроколотую точку сетки . Если все ближайшие точки сетки (т.е. точки, находящиеся на расстоянии меньше, чем ) являются проколотыми, то “нет решений” и идти к шагу 32, иначе − к шагу 21;
21	Вычислить ;
Третий этап (по возрастающему индексу) Определение оптимальной траектории и программного управления
22	Положить ;
23	Организовать цикл по полагаем ;
24	Найти ближайшую к непроколотую точку сетки . Если все ближайшие точки сетки (т.е. точки, находящиеся на расстоянии меньше, чем ) являются проколотыми, то “нет решений” и надо перейти к шагу 32, иначе − к шагу 25;
25	Определить соответствующее ей управление – синтез и полагаем ;
26	Вычислить точку ;
27	Перейти к следующему шагу цикла по , т.е. положить и проверить условие
28	Получить приближение оптимальной траектории и программного управления, вычислить искомое значение функционала I;
29	Проверить точность полученного решения:
30	Для получения более точного решения увеличиваем число точек разбиения множеств . Перейти к шагу 0;
31	− решение задачи. Конец алгоритма.