10.2. Интеграл наложения с использованием переходных характеристик

Обозначим воздействие на электрическую цепь как , а реакцию цепи как . Пусть также известна переходная характеристика цепи . В зависимости от вида воздействия и реакции переходная характеристика может быть переходным сопротивлением , переходной проводимостью , переходной характеристикой по току или напряжению . Тогда расчет реакции электрической

а)	б)
Рис. 10.6

цепи на воздействие будем проводить следующим образом:

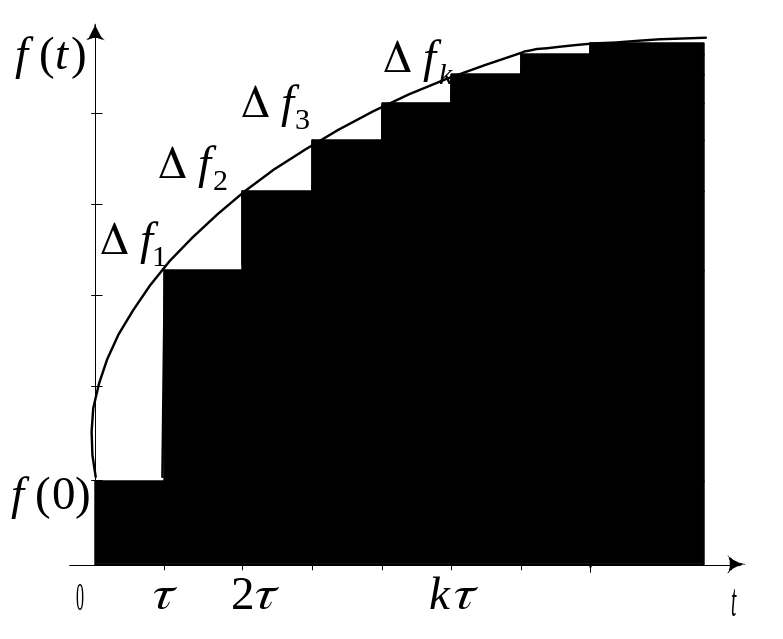
1) приложенное воздействие представим в виде ступенчатых функций , следующих друг за другом через равные интервалы времени (рис. 10.6,а);

2) реакцию цепи на каждое ступенчатое воздействие определяем через переходную характеристику цепи;

3) результирующую реакцию цепи от всей системы ступенчатых воздействий находим исходя из принципа наложения.

В таблице 10.1 показан порядок получения реакции (рис. 10.6,б) цепи от каждого ступенчатого воздействия (рис. 10.6,а).

Таблица 10.1

Временной интервал	Подключенное воздействие	Реакция от подключенного воздействия
…	…	…

Согласно принципу наложения реакцию цепи можно рассчитать, как сумму реакций от каждого ступенчатого воздействия в отдельности:

.

Переходя к пределу с учетом того, что при выполняется и , получим одну из форм интеграла Дюамеля:

. (10.4)

Полученное уравнение (10.4) позволяет вычислить реакцию цепи на заданное воздействие.

Кроме выражения (10.4) существует еще несколько форм интеграла Дюамеля. Вторая форма интеграла Дюамеля может быть получена с помощью теоремы свертки (см. гл. 11):

.

Интегрируя по частям (10.4) запишем еще две формы интеграла Дюамеля:

;

.

Выбор той или иной формы интеграла Дюамеля определяется удобством и простотой вычисления интегралов.

Представленные формы интегралов Дюамеля можно использовать также в случае, когда воздействие задано кусочно-аналитической кривой,

имеющей разрывы в местах стыка. Пусть воздействие задано в виде (рис. 10.7) Используя первую форму записи интеграла Дюамеля (10.4), получим для каждого временного интервала:
	Рис. 10.7

1. при ;

2. при

+ ;

3) при +

Отметим, что используя обобщенные функции, возможно записать формулу для расчета реакции цепи компактнее. Для этого перепишем воздействие в виде

Теперь для вычисления реакции цепи можно пользоваться выражением (10.4), заменяя в нём операцию дифференцирования на обобщенное дифференцирование

.

Пример 10.4

Рассчитать напряжение при подключении цепи (рис. 10.8,а) к источнику напряжения , график которого показан на рис.10.8,б.

Решение

Сначала вычислим переходную характеристику по напряжению . Для этого операторным методом рассчитаем напряжение при

а)	б)
Рис. 10.8		Рис. 10.9

подключении цепи к источнику постоянного напряжения .

Операторная схема замещения показана на рис. 10.9. Операторное изображение входного напряжения . Для цепи на рис. 10.9:

, .

Тогда операторное изображение выходного напряжения

,

где ; .

Оригинал выходного напряжения находим по теореме разложения:

; , ; ; ; .

Таким образом, переходная характеристика по напряжению

.

Для определения реакции цепи на воздействие используем интеграл Дюамеля в виде (10.4):

.

Обозначим , тогда для промежутка выходной сигнал

Для промежутка необходимо учесть скачок напряжения при , тогда

Качественный график временной зависимости напряжения на емкости при условии показан на рис. 10.10.
	Рис. 10.10