Методические указания

к решению контрольных задач

по теоретической механике.

Задача Д-1.

Груз 1 массой m = 0,8 кг укреплён на пружинной подвеске в лифте 2 (жесткости пружин С₁ = 80 Н/м, С₂ = 120 Н/м, С₃ = 160 Н/м). Лифт движется вертикально по закону

z = a₁t² + a₂sint,

где z направлена по вертикали вверх; величина z выражена в метрах, t – в секундах; а₁ = 9,81 м/с², а₂ = 0,2 м,  = 10 ¹/с.

На груз действует сила сопротивления среды R = v, где v – скорость груза по отношению к лифту, коэффициент сопротивления среды  = 8 Нс/м. Вначале грузу сообщается скорость v₀ = 2м/с.

Вес соединительной планки между пружинами и пружин не учитывается.

Найти закон движения груза по отношению к лифту.

Р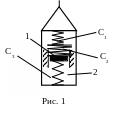 ешение.

1. Решение задачи должно начинаться с замены заданной системы пружин одной эквивалентной пружиной.

Вначале заменим пружины 1 и 2 одной эквивалентной пружиной Э₁. Если вес груза, подвешенного к двум последовательно соединенным пружинам, равен mg, то под действием этой силы, одинаково действующей на обе пружины, пружины растянутся на длину

, (1)

т.е. суммарное удлинение составит . (2)

Эквивалентной пружиной, очевидно, считается такая, удлинение которой равно удлинению заменяемой системы при той же нагрузке.

Растяжение в т. В от силы Р равно растяжению в т. С, где приложена сила Р, т.к. от т. С до т. В (при отсутствии в стержне от т. С до т. В каких-либо сил) происходит только эквидистантное смещение т. С без дальнейшего изменения деформации, т.е.

Δl_B(P) = Δl_С(Р) = Δl_АD(P) + Δl_DC(P). (3)

Каждое из слагаемых в соотношении (3) может быть вычислено по закону Гука:

Δl_АD(P) = Pl_AD/2EF_AD = Pl/2EF, (4)

Δl_DC(P) = Pl_DC/EF_DC = Pl/2EF, (5)

т.е., в соответствии с (3), Δl_В(P) = Pl/EF.

Аналогично вычисляется

Δl_В(R_B) = Δl_BE(R_B) + Δl_ED(R_B) + Δl_DA(R_B) =

= R_B l/E(1/3F+1/F +1/2F) = 11R_Bl/6EF, (6)

и из уравнения совместности деформаций (2) вычисляется «лишнее» неизвестное:

Pl/EF - 11R_Bl/6EF = 0,

R_В = 6Р/11, т.е. R_В = 54,5кН,

а из (1) вычисляется R_А = 5Р/11 = 45,5кН.

Найдя реакции опор стержня, действуя методом сечений, можем построить эпюры усилий, нормальных напряжений и перемещения по длине стержня.

В соответствии с этим методом следует, что на участке АС действует растягивающее усилие (направленное от сечения) N₁ = R_А = 54,5кН, на участке СВ – сжимающее усилие (направленное к сечению) N₂ = R_А - Р = 54,5кН – 100кН =

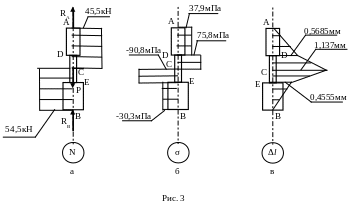
- 45,5кН, численно равное усилию в опоре В. В точке приложения силы Р происходит скачок на эпюре сил на величину этой силы. Эпюра усилий представлена на рис. 3а.

Для дальнейших расчетов необходимо учитывать, что стержень рассчитываемой схемы содержит 4 участка:

1 – участок AD длиной l с усилием N₁ и сечением 2F;

2 - участок DC длиной l/2 с усилием N₁ и сечением F;

3 - участок CE длиной l/2 с усилием N₂ и сечением F;

4 - участок EB длиной l с усилием N₂ и сечением 3F.

Напряжение на каждом участке может быть найдено по формуле

σ_i = N_i/F_i , (7)

т.е. σ₁ = N₁/2F = 45,5×10³/(2×6×10^-4) = 3,79×10⁷Па = 37,9мПа; σ₂ = 75,8мПа; σ₃ = - 90,8мПа; σ₄ = -30,3мПа. Эпюра напряжений представлена на рис. 3б.

Характерной особенностью эпюры напряжений является равенство площадей положительных и отрицательных участков, что является следствием соблюдения условия совместности деформаций.

Деформация по участкам стержня рассчитывается по формуле

Δ_i = N_i l_i/EF_i = σ_i l_i/E, (8)

На первых двух участках имеет место деформация растяжения: Δ₁ = σ₁ l₁/E = 37,9×10⁶×3/2×10¹¹ = 56,85×10^-5м = 0,5685мм, Δ₂ = 75,8×10⁶×1,5/2×10¹¹ = 56,85×10^-5м = 0,5685мм. Таким образом, Δ_АС = Δ₁ + Δ₂ = 1,137мм.

На следующих двух участках имеет место деформация сжатия: Δ₃ = - 90,8×10⁶×1,5/2×10¹¹ = -0,6815мм, т.е. Δ_АЕ = Δ_АС + Δ₃ = 0,4555мм. Далее, Δ₄ = -30,3×10⁶×3/2×10¹¹ = -0,4555мм. Таким образом, Δ_АВ = Δ_АЕ + Δ₄ = 0, что и подтверждает условие совместности деформации.

Эпюра перемещений (деформаций) представлена на рис. 3в.

2. Для определения предельной нагрузки Р_пред для данного стержня при предположении об участке идеальной пластичности на диаграмме растяжения материала стержня заметим по рис. 3б, что максимальное напряжение при Р=100кН (сжимающее) возникает на третьем участке и равно σ₃ = - 90,8мПа. При идеальной пластичности материала стержня напряжение на любом участке пропорционально действующему на этом участке усилию. Отсюда следует, что предельно допустимое напряжение [] = 160МПа в стержне рассматриваемой схемы возникнет, если вместо силы Р к этому стержню будет приложена сила Р_пред = Р×[]/σ₃ = 100×160/90,8 = 176кН.

3. Для определения опорных реакций, возникающих только от действия собственного веса стержня, отбросим силу Р и изобразим на схеме силы веса трех участков с постоянными сечениями, приложив их, естественно, в середине каждого участка (рис. 4а).

Значение веса каждого участка в общем случае находится по формуле

G_i = γ_i×l_i×F_i , (9)

а в данной схеме, при γ_i = γ = const, l_i = l =const, F₁=2F, F₂=F, F₃=3F, имеем:

G₁ = 2γlF, G₂ = γlF, G₃ = 3γlF, G_Σ = 6γlF. (10)

В силу линейности формул (8) и (9), определяющих деформацию участка стержня и вес этого участка, от длины участка, его деформацию можно рассчитывать, считая вес сосредоточенной силой, приложенной в середине длины участка. Таким образом, вес

каждого участка растягивает свой участок на длине, равной половине длины участка.

Очевидно, что веса нижележащих участков растягивают вышележащий участок на всей его длине.

И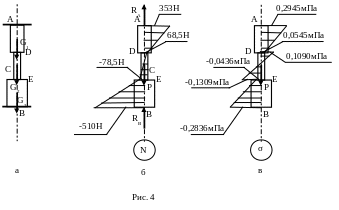 сходя из этого, формула для расчета полной деформации стержня от действия веса при отброшенной опоре В принимает вид:

Δl_АB(G) = Δl_AD(G₁) + Δl_АD(G₂+G₃) + Δl_DE(G₂) + Δl_DE(G₃) + Δl_EB(G₃) =

= [G₁/(2F₁)+(G₂+G₃)/F₁+G₂/(2F₂)+G₃/F₂+G₃/(2F₃)] l/E,

т. е., с учетом (10)

Δl_АB(G) = [2γlF/(2×2F)+4γlF/(2F)+γlF/(2×F)+3γlF/F+3γlF/(2×3F)] l/E = 13γl²/2E. (11)

Итак, формула (11) определяет полное удлинение рассматриваемого стержня от действия веса при отсутствии опоры В. Если снять вес и приложить в т. В силу реакции R_B, деформация стержня по-прежнему будет определяться формулой (6). Условие совместности деформаций вида (2) дает соотношение

11R_Bl/6EF = 13γl²/2E,

или R_B = 39γlF/11. (12)

Из уравнения статики R_A + R_B = G_Σ

получаем, с учетом (10), R_А = 27γlF/11. (13)

Для построения эпюры продольных сил в соответствии с заданными величинами и

равенствами (10), (12), (13) имеем:

N₁ = R_А = 27γlF/11 = 27×8×10⁴×3×6×10^-4 = 353Н;

N₂ = R_D = R_А –G₁ = 27γlF/11 -2γlF = 5γlF/11 = 65,5H;

N₃ = R_E = R_D –G₂ = 5γlF/11 -γlF = -6γlF/11 = -78,5H;

N₄ = R_B = R_E –G₃ = -6γlF/11 -3γlF = -39γlF/11 = -510H.

Эта эпюра представлена на рис. 4б.

Для построения эпюры напряжений по длине стержня полученные выше значения продольных сил, действующих в сечениях стержня, делятся на величину площади соответствующего сечения. При этом в сечениях D, E вначале деление производится на величину площади вышележащего участка, а затем на величину площади нижележащего участка, т.е. в этих точках на эпюре напряжений будут скачки напряжений, соответствующие скачкам величины площади поперечного сечения стержня. Таким образом, получаем значения напряжений, представленные на рис. 4в.

σ(А) = N₁/2F = 27γlF/(11×2F) = 27γl/22 = 27×8×10⁴×3/22 = 0,2945мПа;

σ(D) = N₂/2F = 5γlF/(11×2F) = 5γl/22 = 0,0545мПа;

σ(D') = N₂/F = 5γlF/(11×F) = 10γl/22 = 0,1090мПа;

σ(E) = N₃/F = -6γlF/(11×F) = -12γl/22 = -0,1309мПа;

σ(E') = N₃/3F = -6γlF/(11×3F) = -4γl/22 = -0,0436мПа;

σ(B) = N₄/3F = -39γlF/(11×3F) = -26γl/22 = -0,2836мПа;

Характерная особенность эпюры напряжений - равенство площадей положительных и отрицательных участков, - вытекающая из условия совместности деформаций, справедлива и для эпюры рис. 4в, что может быть проверено соответствующими подсчетами.

Задача С-1.

К кронштейну с стержнями 1 и 2, веса которых не учитываются, приложена сила Р=15кН. Найти усилия в стержнях F₁ и F₂. Углы, обозначенные на схеме, имеют величины: =24°, =39°, =23°.

Решение.

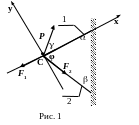
Задача может быть решена несколькими способами. Рассмотрим три из них.

1. Мысленно вырежем т. С и рассмотрим ее равновесие под действием заданной и искомых сил. Аналитические условия равновесия т. С под действием пучка сил (Р, F₁, F₂) в проекциях на оси х, у записываются:

ΣХ = 0; Psin-F₁+F₂cos φ = 0;

ΣY = 0; Pcos-F₂sin φ = 0. (1)

Следует обратить внимание на выбор системы координатных осей х, у. На рис.1 они выбраны таким образом, чтобы одна из осей прошла бы вдоль одного из стержней. В таком случае в системе (1) одно из уравнений непосредственно дает величину одной из двух неизвестных, после чего из второго уравнения находится вторая искомая величина.

Очевидно, φ =180° - (+ ) = 119°. Подстановка всех данных в систему (1) дает:

15sin23°-F₁+F₂cos119° = 0,

15cos23°-F₂sin119° = 0,

откуда F₂ = [кН]; F₁= 15*0,3907 – 15,78*0,4848=-1,7896 [кН].

Знак F₁ показывает, что на самом деле вектор этой силы направлен в противоположном направлении относительно направления, показанного на рис. 1.

Для следующих двух способов, связанных с геометрическими построениями, необходимо схему кронштейна представлять не произвольно, как на рис. 1, а изображать в соответствии с заданными величинами углов , , .

φ

Определим усилия и напряжения в стержнях крепления жесткой балки ОВ на схеме рис. 1. Заданные величины: a = 3м, b = 4м, c = 1,5м; длины стержней l₁ = 2м, l₂ = 3м; угол подкоса α = /4; сечения стержней F₁ = 6×10^-4 м², F₂ = 12×10^-4 м². При этом определим:

1. Выразим усилия и напряжения в стержнях через силу Р;

2. Найдем допускаемую нагрузку Р_доп, приравняв большее из напряжений в стержнях допускаемому напряжению [] = 160мПа;

3. Найдем предельную грузоподъемность системы Р_пред, если предел текучести _т = 240мПа.

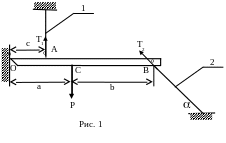
Решение.

1. Пусть Т₁, Т₂ - усилия в стержнях. Если не включать в рассмотрение силы реакций шарнира О, можно составить лишь одно уравнение статики:

Σmom_o(F_i) = 0,

т. е.

сТ₁+(a+b)sin α T₂ – aP = 0. (1)

Вторым уравнением необ-ходимо брать условие сов-местности деформаций, которое в данном случае должно отражать тот факт, что после растяжения (сжатия) стержней 1 и 2 балка ОВ остается прямолинейной. Схематически это положение показано на рис. 2.

Имея ввиду малость деформаций стержней, согласно рис. 1, рис.2 можно составить пропорцию

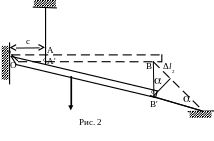АА'/ВВ' = с/(a+b). (2)

Кроме того, из рис. 2 видно, что

АА' = Δl₁, а ВВ' = Δl₂/sinα. (3)

В соответствии с законом Гука

Δl₁ = Т₁l₁/EF₁, Δl₂ = Т₂l₂/EF₂. (4)

Поэтому из (2), (3), (4) следует уравнение совместности деформаций в виде

Т₁ = Т₂сl₂ F₁/[(a+b)l1 F₂sinα]. (5)

Решая совместно уравнения (1), (5), получаем формулы, выра-жающие усилия в стержнях Т₁ и Т₂ через действующую силу Р и заданные геометрические характеристики рассматриваемой схемы:

Т₁ = Рacl₂F₁/[c²l₂F₁+(a+b)²l₁F₂sin²α]; Т₂ = Рa(a+b)l₁F₂sinα/[c²l₂F₁+(a+b)²l₁F₂sin²α]. (6)

Подставляя заданные величины, получаем выражения для усилий в стержнях через значение силы Р:

Т₁ = 0,1289Р; Т₂ = 0,5670Р. (7)

Напряжения в стержнях также могут быть выраж через Р:

σ₁ = Т₁/F₁ = 214,8P, σ₂ = Т₂/F₂ = 472,5P. (8)

2. Из (8) видно, что σ₂ > σ₁. Поэтому по мере возрастания Р именно величина σ₂ первой достигнет допустимого предела [] = 160мПа. Из (8) находится

Р^доп = []/472,5 = 0,339×10⁶Н = 339кН.

3. При дальнейшем возрастании нагрузки Р именно во втором стержне раньше, чем в первом стержне напряжение достигнет значения предела текучести материала - _т = 240мПа. Стержень начнет пластично деформироваться, при этом нагрузка, которую воспринимает этот стержень, будет сохранять постоянное значение

Т₂^пласт = _тF₂ = 240×10⁶ ×12×10^-4 = 288кН. (9)

Конструкция все еще будет способна выдерживать прикладываемую к ней нагрузку, т.к. пластическая деформация одного стержня для нее не критична, поскольку в схеме с одной степенью статической неопределимости один стержень «лишний». Таким образом, нагрузку Р можно увеличивать и далее, но лишь до значения, когда в оставшемся стержне напряжение не станет равным допустимому [] = 160мПа (иначе конструкция претерпит пластическую, т.е. необратимую деформацию). Поэтому предельная нагрузка первого стержня определяется формулой

Т₁^пред = []F₁ = 160×10⁶ ×6×10^-4 = 96кН. (10)

В таком случае предельное значение нагрузки Р в соответствии с (1), (9), (10) определяется:

Р^пред = (с Т₁^пред +(a+b)sin α Т₂^пласт )/а = 523кН.

Следовательно, для конструкции рассмотренной схемы с заданными механическими характеристиками материала стержней предельная нагрузка превышает допустимую в 1,54 раза.

Задача 1-3.

1. Определим крутящие моменты в сечениях стального вала, представленного на схеме рис. 1, и построим эпюру крутящих моментов по длине вала. Заданные величины: a = 3м, b = 4м, c = 1,5м, e = 2м, f = 3м, g = 4м; M₁ = 5,2кНм, M₂ = 2,1кНм, M₃ = 1,1кНм, M₄ = 0,1кНм, M₅ = 1,3кНм.

2. При заданном значении допускаемого напряжения на кручение [] = 35мПа определим диаметры d₁, d₂ и d₃ вала. Построим эпюру действительных напряжений кручения по длине вала.

3. Построим эпюру углов закручивания сечений вала, приняв G = 0,4Е.

Решение.

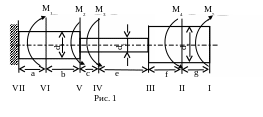
1. Для статически определимой схемы с консольным закреплением вала определение крутящего момента в сечении и построение соответствующей эпюры состоит в алгебраическом суммировании действующих моментов, начиная со свободного конца. Поэтому

М_I-II = M₅ = 1,3кНм;

М_II-IV = M_I-II – M₄ = 1,2кНм;

М_IV-V = M_II-IV – M₃ = 0,1кНм;

М_V-VI = M_IV-V – M₂ = - 2,0кНм;

М_VI-VII = M_V-VI + M₁ = 3,2кНм.

Эпюра крутящих моментов показана на рис. 2.

2. Для определения диаметров d₁, d₂ и d₃ отметим по эпюре рис. 2, что на участке с диаметром d₁ максимальный (по модулю) крутящий момент равен 3,2кНм, на участке с диаметром d₂ - 1,2кНм, а на участке с диаметром d₃ - 1,3кНм.

Из условия прочности при деформации кручения момент сопротивления сечения должен быть определен по соотношению

τ = М_{кр max}/W_p ≤ [], (1)

где W_p – полярный момент сопротивления на кручение, для круглого сечения W_p = πd³/16. Таким образом, диаметр круглого сечения определяется по формуле

. (2)

По этой формуле рассчитываем:

0,0775м;

0,0559м;

0,0574м.

Округляя величины диаметров, выбираем d₁ = 80мм, d₂ = 56мм и d₃ = 60мм. Тогда полярные моменты сопротивления соответствующих участков будут равны:

W_p1 = πd₁³/16 = π×0,08³/16 = 100,5×10^-6м;

W_p2 = π×0,056³/16 = 34,5×10^-6м;

W_p3 = π×0,06³/16 = 42,4×10^-6м.

Действительные максимальные по сечению касательные напряжения по участкам вала находятся из формулы (1):

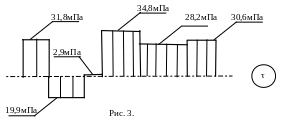
- на участке I – II τ = 1,3×10³ /42,4×10^-6 = 30,6мПа;

- на участке II – III τ = 1,2×10³ /42,4×10^-6 = 28,2мПа;

- на участке III – IV τ = 1,2×10³ /34,54×10^-6 = 34,8мПа;

- на участке IV – V τ = 0,1×10³ /34,5×10^-6 = 2,90мПа;

- на участке V – VI τ = 1,3×10³ /42,4×10^-6 = 19,9мПа;

- на участке VI – VII τ = 1,3×10³ /42,4×10^-6 = 31,8мПа.

Эпюра касательных напряжений представлена на рис. 3.