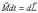Скорость и ускорение. Виды ускорений
Ско́рость— векторная физическая величина, характеризующая быстроту перемещения и направления движения материальной точки в пространстве относительно выбранной системы отсчёта (например, угловая скорость). Этим же словом может называться скалярная величина, точнее модуль производной радиус-вектора.
Ускоре́ние — производная скорости по времени, векторная величина, показывающая, на сколько изменяется вектор скорости точки (тела) при её (его) движении за единицу времени (то есть ускорение учитывает не только изменение величины скорости, но и её направления).
Вектор ускорения материальной точки в любой момент времени находится путём дифференцирования вектора скорости материальной точки по времени:

Ускорение точки при прямолинейном движении
Если
вектор  не
меняется со временем, движение
называют равноускоренным.
При равноускоренном движении справедливы
формулы:
не
меняется со временем, движение
называют равноускоренным.
При равноускоренном движении справедливы
формулы:


II закон Ньютона. Силы в механике.
Второй закон Ньютона — дифференциальный закон движения, описывающий взаимосвязь между приложенной к материальной точке силой и получающимся от этого ускорением этой точки. Фактически, второй закон Ньютона вводит массу как меру проявления инертности материальной точки в выбранной инерциальной системе отсчёта
При подходящем выборе единиц измерения, этот закон можно записать в виде формулы:

где
— ускорение материальной
точки;
 — сила,
приложенная к материальной
точке;
— сила,
приложенная к материальной
точке;
 — масса материальной
точки.
— масса материальной
точки.
Или в более известном виде:

В случае, когда масса материальной точки меняется со временем, второй закон Ньютона формулируется с использованием понятия импульс:
-
В инерциальной системе отсчета скорость изменения импульса материальной точки равна равнодействующей всех приложенных к ней сил.

где  — импульс точки,
— импульс точки,

где  — скорость точки;
— скорость точки;
 — время;
— время;
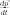 — производная импульса
по времени.
— производная импульса
по времени.
Сила
тяготения

Сила
упругости
III закон Ньютона. При каких условиях сохраняется импульс системы тел? Примеры.
Этот
закон объясняет, что происходит с двумя
взаимодействующими телами. Возьмём для
примера замкнутую систему, состоящую
из двух тел. Первое тело может действовать
на второе с некоторой силой  ,
а второе — на первое с силой
,
а второе — на первое с силой  .
Как соотносятся силы? Третий закон
Ньютона утверждает: сила действия равна
по модулю и противоположна по направлению
силе противодействия. Подчеркнём, что
эти силы приложены к разным телам, а
потому вовсе не компенсируются.
.
Как соотносятся силы? Третий закон
Ньютона утверждает: сила действия равна
по модулю и противоположна по направлению
силе противодействия. Подчеркнём, что
эти силы приложены к разным телам, а
потому вовсе не компенсируются.
Современная формулировка
-
Материальные точки взаимодействуют друг с другом силами, имеющими одинаковую природу, направленными вдоль прямой, соединяющей эти точки, равными по модулю и противоположными по направлению:
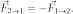
Закон отражает принцип парного взаимодействия. То есть все силы в природе рождаются парами.
Зако́н сохране́ния и́мпульса (Зако́н сохране́ния количества движения) утверждает, что векторная сумма импульсов всех тел (или частиц) замкнутой системы есть величина постоянная.
4. Сила тяжести. Свободное падение. Состояние невесомости и его влияние на организм.
Свобо́дное падéние — равноускоренное движение, под действием силы тяжести.
5. Закон Гука и упругие силы (натяжение нитей и реакции опор). Применение вытяжек при
лечении переломов.
6. Сила трения и коэффициент трения. Трение покоя и трение скольжения.
Тре́ние — процесс взаимодействия тел при их относительном движении (смещении) либо при движении тела в газообразной или жидкой среде.
Сила
трения скольжения — силы,
возникающие между соприкасающимися
телами при их относительном движении.

Тре́ние
поко́я, трение
сцепления — сила,
возникающая между двумя контактирующими телами и
препятствующая возникновению относительного
движения.

7. Пружины, их параллельное и последовательное соединение. Миофибрилла
Коэффициент
упругости по определению равен силе
упругости делённой
на изменение длины пружины. Это можно
записать иначе, в виде формулы:  .
.
Параллельное соединение
При
параллельном соединении
жёсткость  пружин с жёсткостями равными:
пружин с жёсткостями равными:  равна
сумме жёсткостей, то есть
равна
сумме жёсткостей, то есть 
Последовательное соединенение
При
последовательном соединении
жёсткость
пружин
с жёсткостями равными:
равна
единице деленной на сумму обратных
велечин жёсткостей, то есть 
Миофибри́ллы — органеллы клеток поперечнополосатых мышц, обеспечивающие их сокращение.
8. Когда можно говорить о силах инерции? Центрифугирование. Вестибулярный аппарат
человека (отолиты, полукружные каналы).
Вестибулярный аппарат — сложный рецептор вестибулярного анализатора. Структурная основа вестибулярного аппарата — комплекс скоплений реснитчатых клеток внутреннего уха, эндолимфы, включенных в неё известковых образований — отолитов и желеобразных купул в ампулах полукружных каналов. Из рецепторов равновесия поступают сигналы двух типов: статические (связанные с положением тела) и динамические (связанные с ускорением). И те и другие сигналы возникают при механическом раздражении чувствительных волосков смещением либо отолитов (или купул), либо эндолимфы. Обычно отолит имеет большую плотность, чем окружающая его эндолимфа, и поддерживается чувствительными волосками.
9. Центр инерции системы. Баллистокардиография
Баллистокардиографи́я
метод графической регистрации реактивных механических движений тела человека, обусловленных сокращениями сердца и перемещением крови в крупных артериях.
На регистрируемой кривой — баллистокардиограмме (БКГ) отражаются колебания тела, возникающие под влиянием систолы сердца, гидравлического удара крови о дугу аорты и бифуркацию легочного ствола, а затем о бифуркацию аорты. Амплитуда волн БКГ в систолической фазе пропорциональна энергии сердечного выброса.
10. Работа, энергия, мощность. При каких условиях сохраняется энергия системы? Примеры.
11. Чему равна кинетическая энергия тела? В каких единицах она измеряется, и как можно ее
изменить? Привести примеры.
Кинети́ческая эне́ргия — энергия механической системы, зависящая от скоростей движения её точек. Часто выделяют кинетическую энергиюпоступательного и вращательного движения.
.
Работа силы равна изменению кинетической энергии тела.
Это утверждение называют теоремой о кинетической энергии.
Если сила совершает положительную работу, то кинетическая энергия тела увеличивается. Скорость тела при этом возрастает. Если сила совершает отрицательную работу, то кинетическая энергия тела уменьшается. Это происходит, например, при уменьшении скорости тела при действии силы трения.
Кинетическая энергия измеряется в тех же единицах, что и работа, т. е. в джоулях.
12. Гравитационная и упругая потенциальная энергия. В каких единицах она измеряется, и
как можно ее изменить? Привести примеры
Гравитационная энергия — потенциальная энергия системы тел (частиц), обусловленная их взаимным тяготением.
Для
двух тяготеющих точечных тел с
массами M и m гравитационная
энергия  равна:
равна:
,

где:
 —
гравитационная постоянная;
—
гравитационная постоянная;
 —
расстояние
между центрами масс тел.
—
расстояние
между центрами масс тел.
Этот результат получается из закона тяготения Ньютона, при условии, что для бесконечно удалённых тел гравитационная энергия равна 0. Выражение для гравитационной силы имеет вид

где:
 —
сила
гравитационного взаимодействия
—
сила
гравитационного взаимодействия
С другой стороны согласно определению потенциальной энергии:

Тогда:
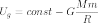
,
Константа в этом выражении может быть выбрана произвольно. Её обычно выбирают равной нулю, чтобы при r, стремящемуся к бесконечности, стремилось к нулю.
Потенциальная энергия упруго деформированного тела. Работа силы упругости. |
Тогда
работа при изменении деформации
от х1 до
х2 равна:
|
Учитывая з-н Гука,
получим:
|
13. Чему равен импульс тела, и как можно его изменить?
В классической механике импульс тела равен произведению массы m этого тела на его скорость v, направление импульса совпадает с направлением вектора скорости:

импульс системы тел могут изменить только внешние силы, причем изменение импульса системы пропорционально сумме внешних сил и совпадает с ней по направлению. Внутренние силы, изменяя импульсы отдельных тел системы, не изменяют суммарный импульс системы.
14. Момент инерции и энергия вращения тела. Движение конечностей тела человека.
Моменты инерции симметричных тел.
15. Момент силы. Рычаги. Виды рычагов в опорно-двигательном аппарате человека.
Момент
силы —векторная физическая
величина,
равная произведению радиус-вектора,
проведенного от оси вращения к
точке приложения силы,
на вектор этой силы. Характеризует
вращательное действие силы на твёрдое тело.

где
—
сила, действующая на частицу,
а  — радиус-вектор частицы.
— радиус-вектор частицы.
16. Уравнение моментов для вращательного движения (II закон Ньютона).
Согласно уравнению второй закон Ньютона для вращательного движения

По
определению угловое ускорение  и
тогда это уравнение можно
и
тогда это уравнение можно
переписать следующим образом
|
Это
выражение носит название основного
уравнения динамики вращательного
движения и формулируется следующим
образом: изменение момента количества
движения твердого тела  ,
равно импульсу момента
,
равно импульсу момента  всех
внешних сил, действующих на это тело.
всех
внешних сил, действующих на это тело.
17. Что такое момент импульса тела? При каком условии сохраняется момент импульса
системы? Привести примеры.
Моме́нт и́мпульса характеризует количество вращательного движения. Величина, зависящая от того, сколько массы вращается, как она распределена относительно оси вращения и с какой скоростью происходит вращение.
Момент
импульса  частицы
относительно некоторого начала отсчёта
определяется векторным
произведениемеё радиус-вектора и импульса:
частицы
относительно некоторого начала отсчёта
определяется векторным
произведениемеё радиус-вектора и импульса:

где  —
радиус-вектор частицы относительно
выбранного неподвижного в данной системе
отсчёта начала отсчёта,
—
радиус-вектор частицы относительно
выбранного неподвижного в данной системе
отсчёта начала отсчёта,  —
импульс частицы.
—
импульс частицы.
Для нескольких частиц момент импульса определяется как (векторная) сумма таких членов:
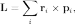
где  —
радиус-вектор и импульс каждой частицы,
входящей в систему, момент импульса
которой определяется.
—
радиус-вектор и импульс каждой частицы,
входящей в систему, момент импульса
которой определяется.
Момент импульса замкнутой системы сохраняется.
18. Виды деформаций. Модуль Юнга. Кривая деформации и разрушение тел. Жевание
коренными зубами и резцами.
Деформация растяжения возникает тогда, когда на стержень или трос действуют внешние силы, приложенные к их концам, направленные в разные стороны и совпадающие с продольной осью этих тел.
Деформация сжатия наблюдается в стержнях относительно коротких под действием внешних сил, направленных навстречу друг другу.
Деформация сдвига возникает тогда, когда на тело, например брусок, действует сила параллельно основанию. В этом случае происходит смещение горизонтальных слоев в теле относительно друг друга без изменения их размеров.
Деформация изгиба
Деформация кручения сопровождается поворотом поперечных сечений стержня вокруг его оси.
Срез — предельный случай сдвига, когда силы упругости не могут уравновесить внешних сил.
Модуль Юнга (модуль упругости) — физическая величина, характеризующая свойства материала сопротивляться растяжению/сжатию при упругой деформации
Модуль Юнга рассчитывается следующим образом:
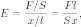
где:
E — модуль упругости, измеряемый в паскалях
F — сила в ньютонах,
S — площадь поверхности, по которой распределено действие силы,
l — длина деформируемого стержня,
x — модуль изменения длины стержня в результате упругой деформации (измеренного в тех же единицах, что и длина l).
19. Уравнение гармонических колебаний и их основные характеристики.
Гармоническое колебание — колебания, при которых физическая (или любая другая) величина изменяется с течением времени по синусоидальному или косинусоидальному закону. Кинематическое уравнение гармонических колебаний имеет вид
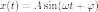
или
 ,
,
где х —
смещение (отклонение) колеблющейся
точки от положения равновесия в момент
времени t; А —
амплитуда колебаний, это величина,
определяющая максимальное отклонение
колеблющейся точки от положения
равновесия; ω —
циклическая частота, величина, показывающая
число полных колебаний происходящих в
течение 2π секунд  —
полная фаза колебаний,
—
полная фаза колебаний,  —
начальная фаза колебаний.
—
начальная фаза колебаний.
20. При каких условиях возникают гармонические колебания? Маятники
Вынужденные — колебания, протекающие в системе под влиянием внешнего периодического воздействия. Примеры: листья на деревьях, поднятие и опускание руки.
Свободные (или собственные) — это колебания в системе под действием внутренних сил, после того как система выведена из состояния равновесия (в реальных условиях свободные колебания всегда затухающие). Простейшими примерами свободных колебаний являются колебания груза, прикреплённого к пружине, или груза, подвешенного на нити.
Параметрические — колебания, возникающие при изменении какого-либо параметра колебательной системы в результате внешнего воздействия.
Случайные — колебания, при которых внешняя или параметрическая нагрузка является случайным процессом.
математический маятник — механическая система, состоящая из материальной точки, подвешенной на невесомойнерастяжимой нити или на невесомом стержне в поле тяжести.
Физический маятник — твёрдое тело, совершающее колебания в поле каких-либосил относительно точки, не являющейся центром масс этого тела, или неподвижной горизонтальной оси, не проходящей через центр масс этого тела.
Маятник Фуко — это груз, подвешенный на нити, способный изменять плоскость своих колебаний.
21. От чего зависят период, частота, амплитуда и начальная фаза колебаний маятника?
22. Почему период колебаний математического маятника не зависит от массы тела,
подвешенного на нити? При каких условиях период колебаний маятника не зависит от
амплитуды?
23. Превращения энергии при гармонических колебаниях? От чего зависит полная энергия
этих колебаний?

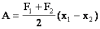 .
.