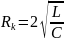8.10. Собственные электрические колебания
Собственные
колебания происходят под действием
начального запаса энергии в системе в
отсутствие внешней вынуждающей силы.
Запишем уравнение закона Ома для
последовательного колебательного
контура (см. рис.8.18):

Рис. 8.18
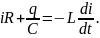
Разделив это
уравнение на
и учитывая,
что
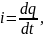
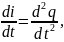
получим
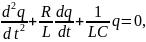
или
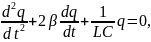
где
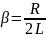
и
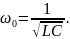
При условии
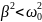 ,
,
решение
дифференциального уравнения имеет вид:
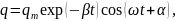
где частота
собственных колебаний
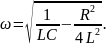
Вывод:
частота
собственных колебаний определяется
электрическими параметрами контура.
Свободные затухающие
колебания заряда конденсатора отражены
графически на рис. 8.19.

Рис. 8.19
Сила тока в контуре
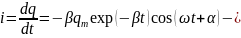
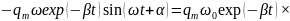
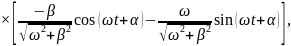
где учтено, что
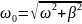 .
.
Введем угол
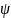 :
:
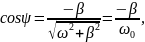
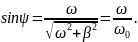
Тогда
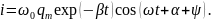
Затухание колебаний
принято характеризовать логарифмическим
декрементом затухания:
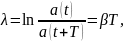
где
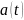 - амплитуда
соответствующей величины (
- амплитуда
соответствующей величины (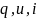 ),
),
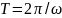 – период
колебаний.
– период
колебаний.
Логарифмический
декремент затухания обратен числу
колебаний
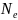 ,
совершаемых
за время, в течение которого амплитуда
уменьшается в
,
совершаемых
за время, в течение которого амплитуда
уменьшается в
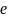 раз:
раз:
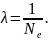
Выразим
этот декремент через параметры контура:
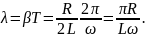
Если затухание
невелико
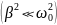 ,
то
,
то
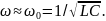 Тогда
Тогда
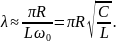
С учетом выражения
для добротности контура
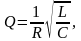 (8.60)
(8.60)
заключаем,
что добротность обратно пропорциональна
логарифмическому декременту затухания:
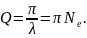
При
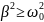 вместо колебаний
происходит апериодический разряд
конденсатора в контуре. Сопротивление
контура, при котором колебательный
процесс переходит в апериодический,
называется критическим.
Значение критического сопротивления
вместо колебаний
происходит апериодический разряд
конденсатора в контуре. Сопротивление
контура, при котором колебательный
процесс переходит в апериодический,
называется критическим.
Значение критического сопротивления
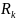 определяется из условия
определяется из условия
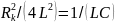 ,
откуда
,
откуда
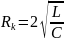



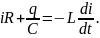
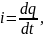
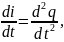
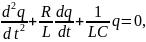
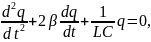
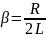
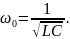
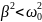 ,
,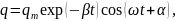
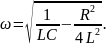

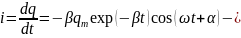
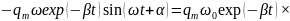
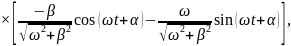
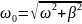 .
.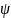 :
: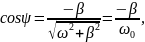
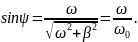
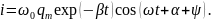
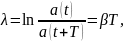
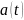 - амплитуда
соответствующей величины (
- амплитуда
соответствующей величины (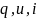 ),
),
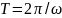 – период
колебаний.
– период
колебаний.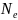 ,
совершаемых
за время, в течение которого амплитуда
уменьшается в
,
совершаемых
за время, в течение которого амплитуда
уменьшается в
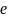 раз:
раз: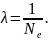
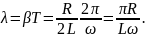
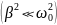 ,
то
,
то
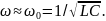 Тогда
Тогда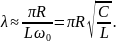
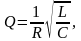 (8.60)
(8.60)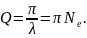
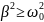 вместо колебаний
происходит апериодический разряд
конденсатора в контуре. Сопротивление
контура, при котором колебательный
процесс переходит в апериодический,
называется критическим.
Значение критического сопротивления
вместо колебаний
происходит апериодический разряд
конденсатора в контуре. Сопротивление
контура, при котором колебательный
процесс переходит в апериодический,
называется критическим.
Значение критического сопротивления
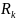 определяется из условия
определяется из условия
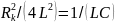 ,
откуда
,
откуда