4.3. Критерий согласия Колмогорова

Критерий Колмогорова используется для проверки гипотезы о предполагаемом законе распределения непрерывной СВ по данным выборки. ЗР должен быть задан в виде непрерывной функции распределения с известными значениями параметров. По данным выборки объёма измерений СВ Х строится статистическая функция распределения СВ Х по формуле , где – количество элементов выборки, значение которых меньше значения аргумента х.

.

Если гипотеза истинна и – заданная теоретическая функция распределения СВ Х, то закон распределения статистики К при бесконечно большом n не зависит от закона распределения СВ Х и называется законом Колмогорова. определяется из .

4.4. Проверка гипотезы об одинаковом распределении двух непрерывных случайных величин

Пусть имеются независимые выборки измерений непрерывных СВ и объёма и соответственно. Рассмотрим критерий Смирнова-Колмогорова, используемый для проверки гипотезы об одинаковом законе распределения СВ и . По данным выборок строятся статистические функции распределения СВ и по формулам , .

.

Если гипотеза истинна, то при бесконечно больших и статистика К независимо от закона распределения СВ и имеет распределение Колмогорова. определяется из .

4.5. Проверка гипотезы о независимости двух случайных величин

Пусть – результаты n-кратных независимых измерений случайного вектора . Пусть множества возможных значений СВ Х и Y разбиты на группы (если Х и Y – дискретные СВ) или интервалы (если Х и Y – непрерывные СВ). Интервалы (группы) значений СВ Х и Y обозначим, соответственно, через и . Количество измерений случайного вектора , при которых СВ Х попала в интервал (группу) , а СВ Y – в интервал (группу) , обозначим .

Определив значения , вычислим величины

и , , , .

имеет распределение . Использовать .

4.6. Проверка гипотез о равенстве математического ожидания и дисперсии нормально распределённой св заданным числам

Пусть Х – случайная величина, имеющая нормальное распределение, а – результаты n независимых измерений этой СВ. Гипотеза о равенстве математического ожидания заданному значению m:

,

Если гипотеза является истинной, то СВ К является дробью Стьюдента с степенями свободы. из условия .

Гипотеза о равенстве дисперсии заданному значению :

.

Если гипотеза является истинной, то СВ К имеет -распределение с степенями свободы. и .

4.7. Проверка гипотезы о равенстве дисперсий двух нормально распределённых св

Пусть Х и Y – случайные величины, которые имеют нормальное распределение и измеряются независимо друг от друга. Пусть – результаты n независимых измерений СВ Х, а – результаты m независимых измерений СВ Y. Пусть и – исправленные дисперсии СВ Х и Y. Тогда в случае истинности выдвинутой гипотезы ( )

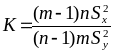
является дробью Фишера с степенями свободы. и .

5.1. Общая характеристика метода метод статистических испытаний

Пусть требуется найти неизвестное значение а изучаемой неслучайной величины. Один из способов решения поставленной задачи состоит в следующем: подбирается случайная величина Х, для которой , генерируется выборка независимых измерений Х, и значение принимается в качестве приближённого значения искомой величины а. Метод Монте-Карло обычно использует для своей работы случайные числа( ) независимых измерений СВ, имеющей равномерное распределение на отрезке .