3.4. Построение доверительного интервала для математического ожидания нормально распределённой св

Пусть – результаты n независимых измерений СВ Х, имеющей нормальное распределение с неизвестными математическим ожиданием и дисперсией. Надо найти для .

Доказано, что при нормальном распределении СВ Х величина является дробью Стьюдента с степенями свободы. Доверительный интервал будем строить в виде , где должно определяться из условия

.

Умножив обе части неравенства на положительную величину , получим 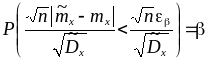, откуда 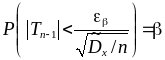. Из таблиц, по известным n и  найдём число из условия . Получим . .

3.5. Построение доверительного интервала для дисперсии нормально распределённой св

Пусть – результаты n независимых измерений СВ Х, имеющей нормальное распределение с неизвестными математическим ожиданием и дисперсией. Надо для . Доказано, что при нормальном распределении СВ Х величина имеет -распределение с степенями свободы. Из таблиц, по известным значениям n и  найдём числа и из условий и .

Тогда .

Следовательно .

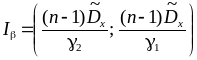4.1. Основные определения и общая схема проверки

Под статистической гипотезой понимается любое предположение о законах или параметрах распределения одной или нескольких СВ.

Ошибка первого рода – это отклонение гипотезы, которая в действительности является верной.

Ошибка второго рода – это принятие гипотезы, которая в действительности не является верной. Вероятности этих ошибок обозначаются, соответственно,  и .

Уровень значимости ‑ вероятность ошибки первого рода ( ).

, но

Статистика критерия ‑ мера расхождения статистических (полученных на основании выборок измерений) и теоретических (предполагаемых) характеристик распределения СВ, относительно которых выдвинута гипотеза.

Допустимая (критическая) область статистики критерия ‑ множество возможных значений, при которых гипотеза принимается (отклоняется). Критическая область определяется неравенствами или и , где – значения статистики, которые при заданном уровне значимости  определяются согласно одному из условий

или .

Общая схема проверки статистической гипотезы:

1) задаётся  и формируются выборки измерений СВ.

2) по данным выборок вычисляется значение статистики К.

3) по  из таблиц распределения статистики К определяются допустимая и критическая области.

4) если вычисленное значение статистики критерия принадлежит допустимой области, то гипотеза принимается, иначе– отклоняется.

4.2. Критерий согласия Пирсона

Критерий Пирсона используется для проверки гипотезы о предполагаемом законе распределения СВ по данным выборки. Этот закон может быть задан с помощью функции, плотности или ряда распределения. Параметры соответствующего закона или задаются заранее, или определяются по данным выборки.

,

где l – число интервалов (групп значений), – объём выборки, – количество элементов выборки, попавших в i-й интервал (i-ю группу значений), – вероятность попадания СВ Х в i-й интервал (i-ю группу значений), вычисленная для предполагаемого закона распределения.

Если гипотеза является истинной, то закон распределения статистики К при бесконечно большом n независимо от закона распределения СВ Х совпадает с , r – количество параметров ЗР, значения которых определяются по данным выборки. из . Недостаток ‑ происходит потеря информации из-за группировки данных выборки по разрядам.