9

1.1. Выборка и статистический ряд

Пусть некоторая СВ Х наблюдается (измеряется) n раз, то есть – независимые СВ, имеющие тот же закон распределения, что и СВ Х.

Генеральная совокупность - все значения, которые может принимать рассматриваемая СВ Х в результате наблюдений (измерений).

Выборкой из генеральной совокупности называются результаты n последовательных независимых наблюдений (измерений) СВ Х.

Вариационным рядом выборки называется запись её элементов в порядке не убывания.

Размах выборки – разность между максимальным и минимальным элементами выборки.

Пусть Х – дискретная СВ. Пусть выборка содержит k различных элементов , записанных в порядке возрастания, причём встречается раз ( ). Число называется относительной частотой элемента .

Статистическим рядом называется последовательность пар , .

Пусть Х – непрерывная СВ. Построив вариационный ряд выборки , возьмём произвольный интервал числовой прямой, охватывающий все элементы выборки с небольшим запасом. Разобьём этот интервал на k непересекающихся интервалов , . Пусть – число элементов выборки, попавших в i-й интервал ( ), тогда число называется относительной частотой интервала .

Рекомендуется брать . Длины интервалов проще брать одинаковыми. Желательно, чтобы каждый интервал содержал не менее пяти элементов выборки.

1.2. Гистограмма и полигон относительных частот

Пусть Х – непрерывная СВ, результаты измерений которой представлены в виде статистического ряда.

Гистограммой относительных частот называется кусочно постоянная функция , которая на каждом из интервалов принимает значение , где , и равна нулю при и при .

Полигоном относительных частот называется функция , графиком которой является ломаная, последовательно соединяющая точки 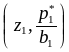, , 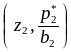. . , . 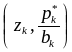Таким образом, график полигона относительных частот – это ломаная, вершины которой расположены на серединах ступеней графика гистограммы относительных частот .

Пусть теперь Х – дискретная СВ, результаты измерений которой представлены в виде статистического ряда, т.е. имеются различные элементы выборки и соответствующие им относительные частоты . Тогда полигоном относительных частот называется функция , графиком которой является ломаная, последовательно соединяющая точки .

1.3. Статистическая функция распределения

Пусть имеется выборка измерений СВ Х. Статистической (эмпирической) функцией распределения называется функция , где n – объём выборки, – количество элементов выборки, значение которых меньше х. – неубывающая кусочно постоянная функция, скачки которой соответствуют значениям СВ Х, имеющимся в выборке, и по величине равны относительным частотам этих значений. Если – минимальный, а – максимальный элемент выборки, то при и при .

Пусть Х – непрерывная СВ. Когда объём выборки измерений достаточно велик, построение становится трудоёмким. Поэтому для получения статистического аналога функции распределения обычно используются данные статистического ряда. Если построены интервалы , и найдены их относительные частоты , , то на правом конце каждого интервала статистическая функция полагается равной , т.е. накопленной относительной частоте этого интервала. При полагается , при полагается . График функции строится в виде ломаной, последовательно проходящей через точки , , , . . , ,

где , и называется кумулятивной ломаной. При большом объёме выборки функции и используются в качестве статистического аналога функции распределения СВ Х.