Физический маятник

Это твердое тело, совершающее колебания вокруг неподвижной оси, жестко связанной с телом. Рассмотрим колебания под действием силы тяжести (рис.4). Выберем положительное направление отсчета угла против часовой стрелки (ось Z направлена к нам). Тогда проекция момента силы тяжести на ось Z запишется, как и уравнение динамики вращательного движения твердого тела примет вид

,

где I — момент инерции тела относительно оси О, l — расстояние между осью О и центром масс С. Ограничимся рассмотрением малых колебаний, при которых sin  . При этом условии предыдущее уравнение можно записать так:

.

Рис.4

Колебания будут гармоническими с частотой ₀ и периодом Т, равными

. (10)

Такую же частоту и период имеет математический маятник длины

, (11)

которую называют приведенной длиной физического маятника.

Точку (рис.4), которая находится на прямой, проходящей через точку подвеса О и центр масс С, и отстоит от точки О на расстоянии l_пр, называют центром качания физического маятника. Центр качания обладает замечательным свойством: если маятник перевернуть и заставить совершать малые колебания вокруг оси , то период колебаний не изменится. На этом свойстве основано определение ускорения свободного падения с помощью оборотного маятника: экспериментально устанавливают положения двух «сопряженных» точек (осей) О и , малые колебания вокруг которых происходят с одинаковой частотой. Это значит, что расстояние О = l_пр. Определив ₀ и l_пр, из формулы находим g.

Общие выводы

Рассмотренные примеры относятся к свободным колебаниям без трения, которые происходят в системе, предоставленной самой себе после того, как она была выведена из состояния равновесия. Можно утверждать, что свободные колебания любого осциллятора в отсутствие трения будут гармоническими, если действующая в нем сила (или момент силы) является квазиупругой, т.е. силой, направленной к положению равновесия и зависящей от смещения из этого положения линейно.

Именно квазиупругий характер силы (или момента силы) служит и критерием малых колебаний.

Кроме того, частота и период свободных колебаний без трения зависят только от свойств самого осциллятора в отличие от амплитуды колебаний и начальной фазы, которые определяются начальными условиями.

Энергия гармонического осциллятора

Рассмотрим этот вопрос на примере материальной точки массы m, колеблющейся под действием квазиупругой силы . Потенциальная и кинетическая энергии частицы имеют в данном случае такой вид:

,

. (12)

Из этих соотношений видно, что значения U и K сдвинуты друг от друга по фазе на /2: когда U максимальна, К минимальна, и наоборот. При этом полная энергия сохраняется:

, (13)

где учтено, что . Принимая во внимание (13), формулы (12) можно переписать так:

. (14)

Графики зависимостей U(t) и K(t) даны на рис.5. Из рисунка видно, что в процессе колебаний происходит переход потенциальной энергии в кинетическую и обратно. Это иллюстрирует и рис.6.

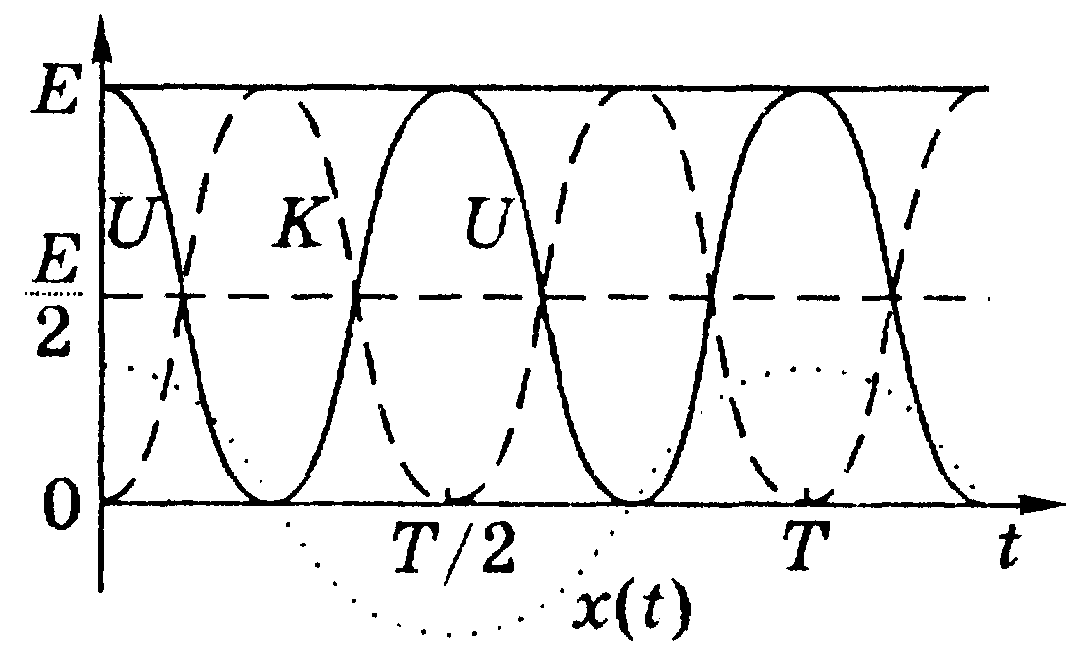
Рис.5

Рис.6

Средние (за период колебания) значения потенциальной и кинетической энергий одинаковы, и каждое из них равно Е/2:

(15)

поскольку известно, что средние (за период) значения квадратов синуса и косинуса равны ½.

Отметим в заключение, что, согласно (13), энергия колебаний осциллятора пропорциональна квадрату амплитуды. Этот важный факт неоднократно учитывается при анализе колебаний.

Энергия и уравнение движения

Уравнение движения колебательной системы можно получить не только из уравнений динамики, но и из закона сохранения энергии Е (иногда это бывает удобнее). Для этого нужно составить выражение для энергии Е, продифференцировать его по времени и потребовать, чтобы dE/dt = 0, поскольку Е = const. Это и приведет к искомому уравнению.

Важно отметить, что колебательная система будет гармоническим осциллятором лишь при условии U пропорционально х², т.е. когда потенциальная энергия пропорциональна квадрату смещения из положения равновесия. Это условие, кстати, является и «энергетическим» критерием малых колебаний.