
- •Колебания Гармонические колебания
- •Динамика гармонических колебаний
- •Грузик на пружине
- •Математический маятник
- •Физический маятник
- •Общие выводы
- •Энергия гармонического осциллятора
- •Сложение гармонических колебаний
- •Затухающие колебания
- •Вынужденные колебания
- •Резонанс
- •Энергия вынужденных колебаний
Колебания Гармонические колебания
Кинематика гармонических колебаний
Гармоническими называют колебания, в которых интересующая нас величина х (например, линейное или угловое смещение из положения равновесия) изменяется со временем t по закону
![]() (1)
(1)
где а – амплитуда,
![]() – фаза, – начальная
фаза,
– фаза, – начальная
фаза,
![]() – циклическая (круговая) частота
колебаний. Эта частота связана с периодом
Т и линейной частотой
как
– циклическая (круговая) частота
колебаний. Эта частота связана с периодом
Т и линейной частотой
как
![]() .
(2)
.
(2)
Линейная частота это количество колебаний в секунду, измеряется в герцах (Гц). Круговая частота показывает, на какое количество радианов изменяется фаза колебаний в одну секунду, измеряется в с-1.
Продифференцировав (1) по времени, найдем
скорость
![]() и ускорение
и ускорение
![]() :
:
![]() ,
(3)
,
(3)
![]() (4)
(4)
Из этих выражений видно, что скорость
и ускорение
также изменяются по гармоническому
закону с амплитудами
![]() и
и
![]() соответственно. При этом скорость
опережает смещение х по фазе на /2,
а ускорение – на ,
т.е. находится в противофазе со смещением
х. На рис.1 приведены графики
зависимостей х(t),
(t),
(t)
для случая = 0.
соответственно. При этом скорость
опережает смещение х по фазе на /2,
а ускорение – на ,
т.е. находится в противофазе со смещением
х. На рис.1 приведены графики
зависимостей х(t),
(t),
(t)
для случая = 0.
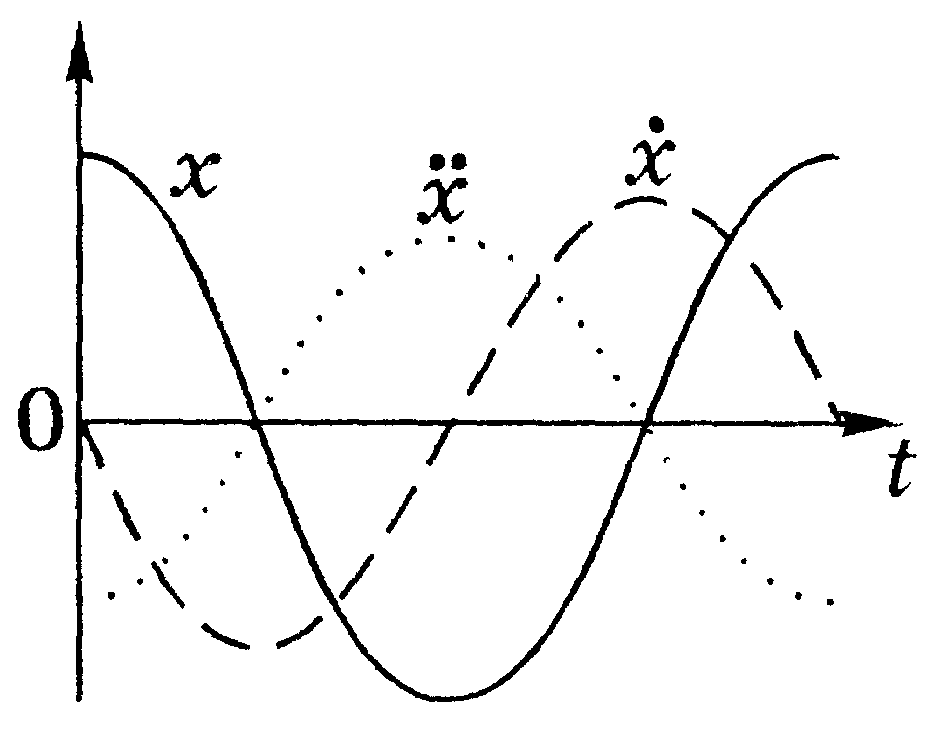
Рис.1
Сопоставив (4) и (1), видим, что
![]()
Это дифференциальное уравнение называют
уравнением гармонического осциллятора.
Его решение (1) содержит две произвольные
постоянные: а и .
Для каждого конкретного колебания они
определяются начальными условиями
смещением х0
и скоростью
![]() в начальный момент t
= 0:
в начальный момент t
= 0:
![]() .
(6)
.
(6)
Отсюда находим искомые постоянные:
![]() (7)
(7)
Обычно рассматривают только значения в интервале (, ). Уравнение для tg удовлетворяется двумя значениями в этом интервале. Из этих значений следует взять то, при котором получаются правильные знаки у cos и sin в (6).
Динамика гармонических колебаний
Для определения характера движения механической системы нужно, исходя из законов динамики или закона сохранения энергии, составить уравнение движения системы, и если оно приводится к виду (5), то можно однозначно утверждать, что данная система является гармоническим осциллятором, частота 0 которого равна корню квадратному из коэффициента при х. Рассмотрим несколько примеров и затем обобщим полученные результаты.
Грузик на пружине
Пусть грузик массы m,
подвешенный на невесомой пружине
жесткости
![]() , совершает вертикальные колебания
(рис.2). Возьмем начало О оси Х в
положении равновесия, где
, совершает вертикальные колебания
(рис.2). Возьмем начало О оси Х в
положении равновесия, где
![]() ,
,
![]()
растяжение пружины в этом положении.
Тогда, согласно основному уравнению
динамики,
растяжение пружины в этом положении.
Тогда, согласно основному уравнению
динамики,
![]() ,
или
,
или
![]() .
.
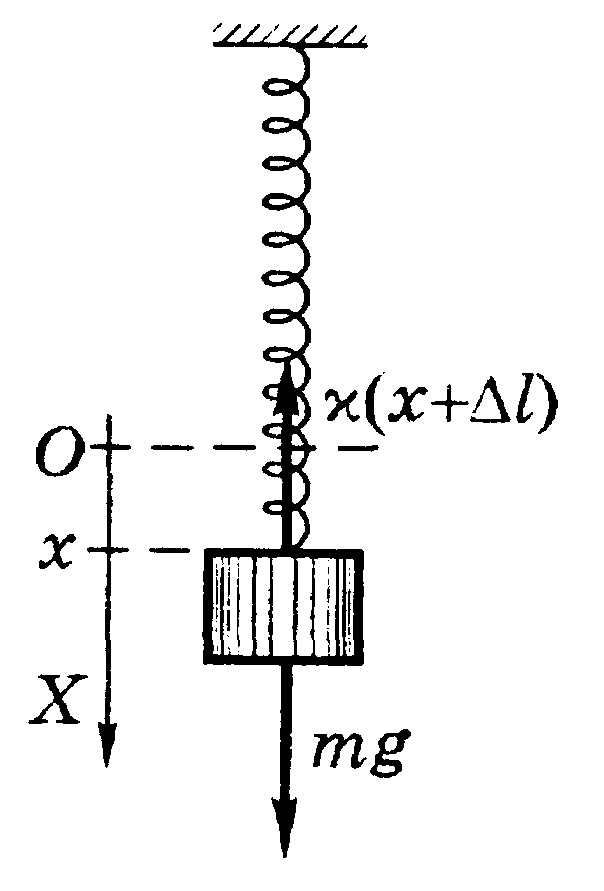
Рис.2
Из сопоставления с (5) видим, что это уравнение гармонического осциллятора, колеблющегося около положения равновесия с частотой 0 и периодом Т, равными
![]() ,
,
![]() (8)
(8)
Математический маятник
Материальная точка массы m,
подвешенная на нерастяжимой нити длиной
l, совершает колебания
в вертикальной плоскости (рис.3). Здесь
удобнее всего использовать уравнение
динамики в проекции на орт ,
направление которого совпадает с
положительным направлением дуговой
координаты s (величина
алгебраическая, на рисунке изображен
момент, когда s
0). Начало отсчета s
возьмем в положении равновесия — в
точке О. Имея в виду, что s
= l![]() ,
,
![]() и что проекция силы натяжения F
= 0, запишем:
и что проекция силы натяжения F
= 0, запишем:
![]() ,
или
,
или
![]()
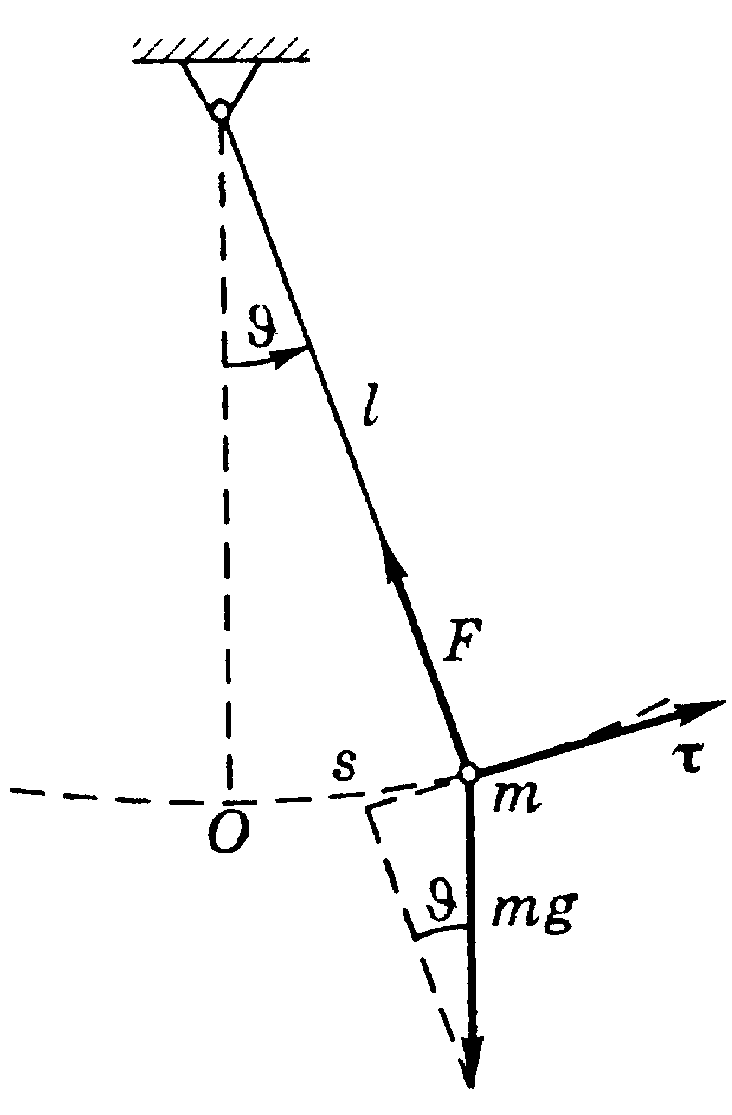
Рис.3
Из сопоставления с (5) видим, что это уравнение, вообще говоря, не является уравнением гармонического осциллятора. Поскольку в нем вместо смещения стоит sin . Однако при малых колебаниях, когда sin , уравнение совпадает с (5):
![]() ,
,
откуда следует, что частота 0 и период Т математического маятника, совершающего малые колебания, равны
![]() .
(9)
.
(9)
