Лабораторна робота № 1 встановлення законів розподілу параметрів елементів і компонентів апаратури
1 Мета роботи
Вивчити методику визначення законів розподілу у великій партії елементів і компонентів РЕА і опанувати її; визначити коефіцієнти Бородачева досліджуваних параметрів виробів.
2 Загальні відомості
Позначимо
через 
значення параметра деякого виробу
(елементу конструкції). Оскільки за
своєю природою
− випадкова величина, то при дослідженні
закону розподілу параметра або його
числових характеристик (математичного
очікування, дисперсії і тому подібне)
використовується апарат математичної
статистики.
Партію однорідних виробів, для якої досліджується закон розподілу, назвемо генеральною сукупністю. При масовості виробництва генеральна сукупність містить велике число елементів − до сотень тисяч і мільйонів, тому оцінку закону розподілу виконують по випадковій вибірці з генеральної сукупності. Оцінка, отримана за результатами вимірів параметрів у вибірці, називається вибірковою оцінкою, а число виробів, що потрапили у вибірку, − об'ємом вибірки.
Найбільш
повну інформацію про можливі значення
параметра у великій партії містить
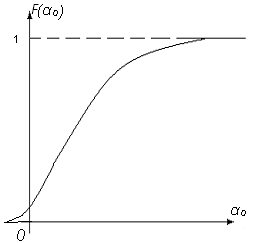
закон розподілу вірогідності. Інтегральна
форма цього закону, так звана функція
розподілу,
визначає вірогідність того, що випадкова
величина набуде якого-небудь значення
з інтервалу 
,
тобто 
.
Функція
як і всяка вірогідність, не може набувати
від’ємних значень: 
;
величина
знаходиться у межах 
.
Крім того 
є неспадаючою функцією аргументу,
оскільки із зростанням 
вірогідність того, що
набуде значення з інтервалу 
або зросте, або не зміниться. При 
функція
необмежено наближається до одиниці
(рис.1.1).
У ряді випадків зручніше оперувати не функцією розподілу, а її похідною − так званою щільністю розподілу вірогідності:
Вираз
для вірогідності того, що випадкова
величина набуде значення з деякого
інтервалу 
,
можна записати у виді
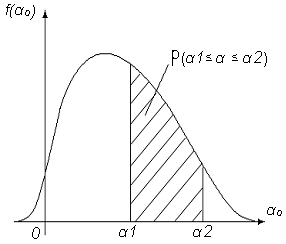
Таким чином, ця вірогідність оцінюється площею під кривою щільності розподілу вірогідності, яка опирається на інтервал (рис. 1.2).
|
|
Рис. 1.1 Функція розподілу |
Рис. 1.2 Щільність розподілу вірогідності |
Щільність
розподілу вірогідності, як похідна, від
неспадаючої функції
завжди невід’ємна: 
.
Явно
Припущення про вид розподілу потрібні для вибору конкретних методів обробки вибірки. Вид закону встановлюється не з математичних міркувань, а виходячи з фізичної суті процесів, що визначають випадковий характер даного параметра. Найчастіше зустрічаються наступні види розподілів.
1. Розподіл Гауса − вид розподілу випадкової величини, коли вона викликана підсумовуванням досить великої кількості чинників без істотного переважання одного над іншими. Багато його застосувань обумовлено центральною граничною теоремою теорії вірогідності (теорема Ляпунова). Зазвичай на практиці достатньо, щоб кількість чинників складала 5-6.
Функція щільності розподілу Гауса має вигляд
де
− математичне
очікування; 
−
середньоквадратичне відхилення параметра
.
2. Розподіл Релея існує у тому випадку, коли параметр має фізичне одностороннє обмеження і формується за рахунок декількох чинників, розподілених за законом Гауса. Функція щільності описується виразом
3. Рівномірний розподіл виникає у разі істотного двостороннього обмеження на значення параметра, наприклад у випадку регулювання. Функція щільності має вигляд
4. Логарифмічно нормальний розподіл − розподіл величини, логарифм якої має нормальний розподіл, − виникає у параметрів, схильних до зносу (старінню). Описується виразом
причому
математичне очікування дорівнює 
.
5.
Експоненціальний розподіл є розподілом
часу між подіями, що з'являються з
постійною інтенсивністю. Функція
щільності має вигляд 
і математичне очікування рівне 
.
Для
опису закону розподілу найчастіше
використовують числові характеристики
розподілу, а саме математичне очікування
і
дисперсію 
.
Математичне очікування характеризує
положення центру групування величини
,
а дисперсія (середньоквадратичне
відхилення)
− розсіяння відносно центру.
При визначенні числових характеристик законів розподілу є важливими такі властивості вибіркових оцінок як спроможність, незміщеність і ефективність. Спроможною вибірковою оцінкою числової характеристики називають оцінку, яка при зростанні об'єму вибірки прагне до істинного значення числової характеристики в генеральній сукупності, а точніше сходиться по вірогідності з ним. Вибіркову оцінку роблять по вибірці обмеженого об'єму. Якщо з генеральної сукупності здійснити повторну вибірку того ж об'єму, то найімовірніше, що та ж оцінка набуде дещо відмінне значення, від попереднього. Таким чином, вибіркова оцінка є випадковою величиною, що міняється від вибірки до вибірки.
Вибіркові оцінки, що мають ту властивість, що при будь-якому об'ємі вибірки їх математичне очікування рівно оцінюваній числовій характеристиці, називаються незміщеними оцінками. Вимога незміщеності оцінки особлива важливо при малому об'ємі вибірки, коли величина зміщення може спотворити результати.
Велике значення для встановлення міри якості того або іншого способу оцінки числової характеристики належить поняттю ефективності вибіркової оцінки. Щоб оцінка була ближча до істинного значення числової характеристики, необхідно, щоб закон розподілу вірогідності для вибіркової оцінки випадкової величини був по можливості "сконцентрований" поблизу істинного значення оцінюваної характеристики, тобто треба, щоб розсіювання вибіркової оцінки при багатократному повторенні вибірки було по можливості менше. Оцінка, що має менше розсіювання (дисперсію) відносно істинного значення, називається ефективнішою оцінкою.