4.1.4. Колебательные спектры двухатомных молекул

Инфракрасные спектры обычно изображаются в виде зависимости оптической плотности D (в англоязычной литературе принято обозначение A – absorbance) от волновых чисел .

Согласно закону Бугера – Ламберта – Бера, оптическая плотность пропорциональна концентрации поглощающего вещества:

,

где  – коэффициент экстинкции (л моль^–1 см^–1), С – концентрация (моль/л), l (см) – толщина поглощающего слоя.

ИК спектр двухатомной молекулы в области основных тонов содержит одну широкую полосу, состоящую из двух ветвей (P- и R-ветви), обусловленную колебательным переходом с уровня  = 0 на уровень  = 1 (рис. 4.5). Каждая ветвь состоит из большого числа узких линий, образующих вращательную структуру. Каждая линия в пределах этой полосы соответствует переходу из исходного колебательно-вращательного состояния в конечное колебательно-вращательного состояние. При этом в соответствии с правилами отбора, вращательное квантовое число J при переходе изменяется на единицу (увеличивается или уменьшается) J = 1.

Последнее кажется удивительным, поскольку закон сохранения момента импульса является столь же строгим, как и законы сохранения энергии и импульса. Между тем при переходе J = 1 состояние вращения молекулы изменяется. Правда, в исходном состоянии в системе был ещё фотон, а в конечном состоянии его не стало. Остаётся предположить, что избыточный момент импульса «прилетел» с фотоном, т. е., иначе говоря, что фотон обладает собственным моментом импульса. Это правда. Фотон действительно может находиться в двух спиновых состояниях с проекцией спина на направление движения ±1. (Этому свойству в классической электродинамике соответствует круговая правая и левая поляризация электромагнитной волны.) После поглощения фотона двухатомной молекулой момент количества движения передаётся ей. Поэтому если она покоилась, то после поглощения фотона – должна начать вращаться. Таким образом, опыт, который вы сейчас проделаете, доказывает наличие спина у фотона.

Если молекула имеет нечётное число электронов (например, NO), правило отбора изменяется. В этом случае возможны переходы, для которых J = –1, 0, +1. Это согласуется с тем, что спин электрона = ½. В колебательно-вращательном спектре NO между P- и R-ветвями имеется интенсивная линия, называемая Q-ветвью.

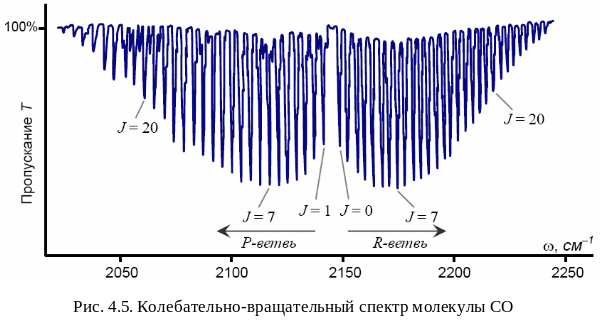
В соответствии с правилом отбора (J = 1) между вращательными состояниями разных колебательных уровней осуществляются две серии переходов, одну из них обозначают R-ветвь (J = +1), другую P-ветвь (J = –1). R-ветвь (J = +1) всегда расположена со стороны бóльших частот, первая наблюдаемая линия соответствует исходному состоянию J = 0. P-ветвь (J = –1) расположена со стороны меньших частот, первая наблюдаемая линия соответствует исходному состоянию J = 1. Классификация идёт по квантовому числу исходного состояния.

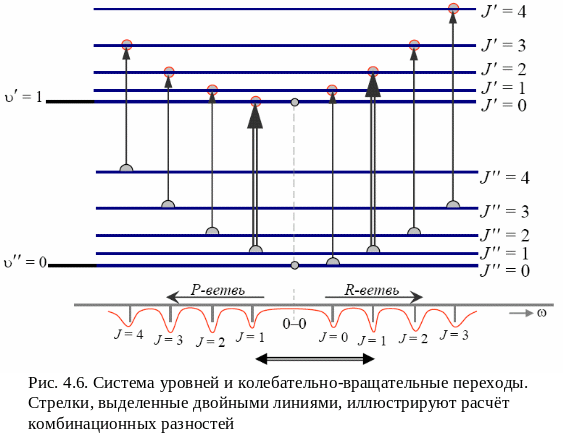
Между R- и P-ветвями находится промежуток (Q-ветвь), который соответствует чисто колебательному переходу J = 0, запрещённому правилами отбора для двухатомных молекул имеющих чётное число электронов. Рис. 4.6 поясняет, какие колебательно-вращательные переходы приводят к появлению пиков в R-ветви и P-ветви.

Поскольку нас интересует область, соответствующая переходу с нулевого колебательного уровня ( = 0) на первый ( = 1), для расчёта колебательно-вращательной энергии молекулы целесообразно использовать приближение гармонического осциллятора (1) и колеблющегося ротатора (2):

где ₀ – частота колебательного перехода с уровня  = 0 на уровень  = 1.

В этом приближении колебательно-вращательная энергия молекулы при разных значениях J для первого ( = 1) и нулевого ( = 0) колебательных уровней равна, соответственно:

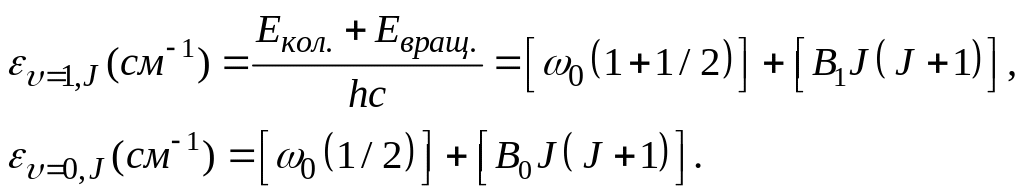(4.3)

Отсюда можно вычислить положение линий в R-ветви и Р-ветви. Учтём, что вращательные квантовые числа, относящиеся к исходному уровню, принято обозначать символом J , к конечному – J .

Положение линий в R-ветви, для которой J  = J + 1:

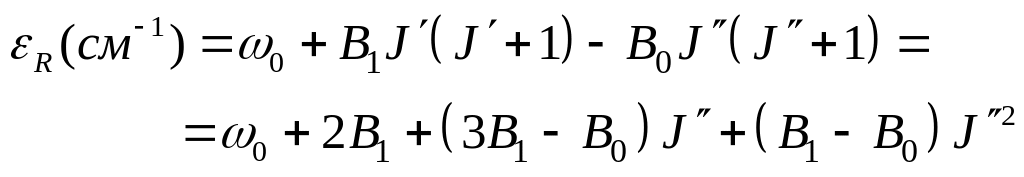(4.4)

Положение линий в Р-ветви, для которой J  = J – 1, вычисляется аналогично:

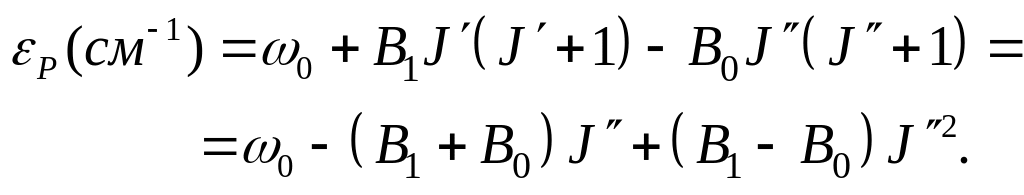(4.5)

Вследствие колебательно-вращательного взаимодействия (см. раздел 4.1.3.) всегда выполняется соотношение и разность этих величин имеет отрицательное значение . Следовательно, с ростом J линии вращательной структуры в R-ветви постепенно сходятся, а в Р-ветви расходятся (это видно из рис. 4.5). Для первых нескольких значений J можно пренебречь взаимодействием колебаний с вращением и принять , тогда имеем:

В этом приближении расстояние между соседними линиями вращательной структуры равно 2В, как и в чисто вращательных спектрах.

Для определения вращательных постоянных и из колебательно-вращательных спектров пользуются методом комбинационных разностей ₂F(J), которые рассчитываются по формулам:

,

,

где обозначает положение линий (в см^–1) с вращательным числом J в R-ветви, а – положение линий в P-ветви. Как можно видеть из рис. 4.6, комбинационные разности ₂F  и ₂F  – это расстояние между линиями в P- и R-ветвях, которые относятся к одному и тому же конечному (₂F ) или начальному (₂F ) состоянию. На рис. 4.6 это расстояние, измеряемое в см^–1, показано горизонтальной стрелкой. Выделены два перехода, относящихся к P- и R-ветвям, для которых начальным состоянием является J = 1. Из формул (4) и (5) можно получить следующие выражения, связывающие ₂F и вращательную постоянную в приближении колеблющегося ротатора:

(4.6)

Таким образом, ₂F(J) линейно зависит от (J + 1/2). Рассчитав из колебательно-вращательного спектра несколько значений ₂F  или ₂F  легко определить вращательную постоянную или .

Дополнительное уточнение можно получить, привлекая модель нежёсткого ротатора. В этом случае вместо (6) имеем:

(4.7)

что эквивалентно линейному уравнению y = a + bx, в котором Таким образом, из отсекаемого отрезка а определяется вращательная постоянная В_, а из наклона аппроксимирующей прямой b – постоянная центробежного растяжения D_. Соотношение (7) следует использовать при обработке спектров HCl. В случае CO оно не даёт заметной разницы с результатом, полученным по соотношению (6). В случае NO обработка данных по уравнению (6) даёт правильное значение B, а уравнение (7) неприменимо. Причина поясняется в описании лабораторной работы ИК-1.