
- •1. Тепловые процессы при сварке
- •2. Основы теории теплопроводности
- •2.1. Основные понятия
- •2.2.Закон теплопроводности Фурье
- •2.3. Дифференциальное уравнение теплопроводности
- •3. Математическая постановка краевых задач теплопроводности
- •3.1. Условия однозначности
- •3.2. Краевые условия
- •4. Математическое описание наиболее распространенных сварочных источников тепла
- •4.1. Дельта-функция Дирака
- •4.2. Описание сварочных источников тепла
- •4.2.1. Форма сварочных источников теплоты
- •4.2.2. Математическое описание некоторых неподвижных источников теплоты
- •5. Построение тепловых математических моделей с использованием метода функций Грина
- •5.1. Общее описание метода функций Грина
- •5.2. Построение функций Грина
- •Нестационарных тепловых процессов
- •6. Одномерные задачи теплопроводности со сварочными источниками тепла
- •6.1. Нагрев бесконечного стержня мгновенным точечным источником
- •6.2. Нагрев конечного стержня мгновенным точечным источником тепла
- •6.3. Нагрев конечного стержня непрерывно-действующим точечным источником
- •6.4. Нагрев стержня проходящим током.
- •7. Трехмерные математические модели
- •7.1. Нагрев бесконечной пластины, ограниченной по z мгновенным неподвижным точечным источником
- •7.2. Нагрев бесконечной пластины непрерывно-действующим подвижным нормально-круговым источником
- •7.3. Нагрев бесконечной пластины непрерывно-действующим линейным по глубине (оси z) источником
3.2. Краевые условия
Начальное условие определяется заданием закона распределения температуры внутри тела в начальный момент времени, т.е.
![]()
Во многих задачах принимают равномерное распределение температуры в начальный момент времени
![]()
Граничное условие может быть задано различными способами.
Граничное условие I рода состоит в задании распределения температуры по поверхности тела в любой момент времени и математически описывается следующим образом
![]() ,
,
где
![]() -
температура на поверхности тела.
-
температура на поверхности тела.
В частном
случае
![]() ,
т.е температура на поверхности постоянна
на протяжении всего процесса теплообмена.
Это может быть осуществлено при
искусственном поддержании постоянной
температуры или при особых условиях
теплообмена между окружающей средой и
поверхностью тела.
,
т.е температура на поверхности постоянна
на протяжении всего процесса теплообмена.
Это может быть осуществлено при
искусственном поддержании постоянной
температуры или при особых условиях
теплообмена между окружающей средой и
поверхностью тела.
Граничное условие II рода состоит в задании плотности теплового потока для каждой точки поверхности тела, как функции времени, т.е.
![]()
Простейший случай граничного условия второго рода состоит в постоянстве плотности теплового потока:
![]()
Такой случай имеет место, например, при нагревании тел в высокотемпературных печах.
Граничное условие III рода характеризует закон конвективного теплообмена между поверхностью тела и окружающей средой при постоянном потоке тепла. В этом случае количество тепла, передаваемого в единицу времени с единицы площади поверхности тела в окружающую среду с температурой Tc в процессе охлаждения (Tn > Tc), прямо пропорционально разности температур между поверхностью тела и окружающей средой, т.е.
![]() ,
,
где
![]()
коэффициент пропорциональности,
называемый коэффициентом теплообмена.
коэффициент пропорциональности,
называемый коэффициентом теплообмена.
4. Математическое описание наиболее распространенных сварочных источников тепла
4.1. Дельта-функция Дирака
Рассмотрим функцию
![]() ,
имеющую максимум при
,
имеющую максимум при
![]() ,
быстроубывающую в обе стороны от
,
и такую, что
,
быстроубывающую в обе стороны от
,
и такую, что![]() .
Эти условия не определяют вид функции
.
Эти условия не определяют вид функции
![]() ,
так как можно привести несколько функций,
удовлетворяющих поставленным выше
требованиям, например:
,
так как можно привести несколько функций,
удовлетворяющих поставленным выше
требованиям, например:
![]() ;
;
![]()
Можно доказать, например, что во
второй функции
![]() ,
тогда числовой множитель обеспечивает
равенство интеграла единице. График
этой функции приведен на рис.2.
,
тогда числовой множитель обеспечивает
равенство интеграла единице. График
этой функции приведен на рис.2.
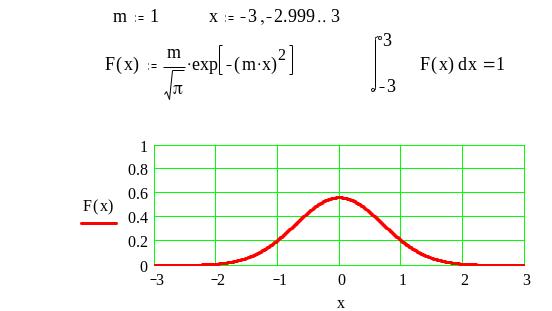
Рис.2
Произведем над линией
![]() следующее преобразование: увеличим ее
высоту в m раз и одновременно
уменьшим ее ширину во столько же раз. В
этом случае уравнение приобретает вид
следующее преобразование: увеличим ее
высоту в m раз и одновременно
уменьшим ее ширину во столько же раз. В
этом случае уравнение приобретает вид
![]() .
Например, из рассмотренного выше
уравнения получим
.
Например, из рассмотренного выше
уравнения получим
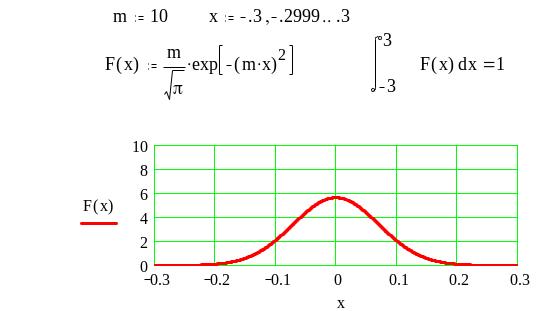
Рис.3
Видно, что площадь, заключенная между графиком и осью х, при растяжении кверху увеличивается в m раз, а при сжатии с боков уменьшается во столько же раз, т.е. в конечном итоге останется без изменений. Впрочем, это легко доказывается и с помощью интегрирования после замены переменной интегрирования mxs.
При любом фиксированном х0 величина будет неограниченно приближаться к нулю при неограниченном росте m (см. рис.4)
Р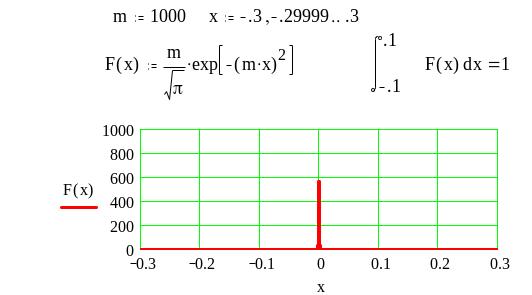 ис.
4
ис.
4
Следовательно, неограниченно увеличивая m, мы получаем функцию со следующими свойствами:
функция равна нулю при всех x<0 и при всех х>0;
функция бесконечна при x0;
интеграл от этой функции, взятый в пределах от - до +, равен
Функции, обладающие этими свойствами, называется дельта-функцией Дирака и обозначается через (х). Для применения (х) достаточно знать три ее свойства, перечисленные выше, и совершенно не требуется знать, из какой именно функции она получена. Можно сказать, что (х) – это функция, принимающая на узком участке большие значения, причем эти значения согласованы с шириной участка так, что выполняется условие 3.
Из свойств (х) следует основное соотношение
![]() .
.
Так как (х) 0 при всех х 0, то
![]() ,
,
где - малая величина.
Необходимо отметить, что (х-а) отлично от нуля (и притом бесконечно) только при х а. По аналогии с формулой (1) получим
![]()
Дельта-функцию можно рассматривать
также на плоскости и в пространстве.
Например, в пространстве под функцией
![]() на до понимать функцию, равную нулю
всюду вне начала координат (0,0,0), равную
бесконечности в начале и при том такую.,
что интеграл от нее по всему пространству
равен единице. Этим условиям удовлетворяет
функция
на до понимать функцию, равную нулю
всюду вне начала координат (0,0,0), равную
бесконечности в начале и при том такую.,
что интеграл от нее по всему пространству
равен единице. Этим условиям удовлетворяет
функция
![]()
![]()
Таким образом, тепловой поток q, сосредоточенный в точке (a, b, c), можно рассматривать как тепловой поток, распределенный в пространстве с плотностью
![]()
