Стратегия "круговая оборона".
Когда ЛПР не знает, как следовать сконцентрировать ресурсы, оно распыляет их по всем направлениям. Это оправдано только в том случае, когда ситуация действительно обладает очень высокой неопределенностью.
Принятие решений на основе сравнения матожиданий.
Риск оценивается как матожидание потерь, то есть как сумма возможных потерь, умноженных на вероятность этих потерь. Решение принимается в пользу наименьшего, таким образом оцененного, риска. Это метод оправдан, если: а) вероятности точно известны, б) однотипные решения принимаются многократно, в) ни одно из принятых решений не может быть фатальным для ЛПР.
Основные понятия матем теории принятия решений.
Будем полагать,
что лицо, принимающее решение (ЛПР),
имеет возможность выбора из вариантов
своих действий а1,
а2 …
аm.
В ответ некий противник выдает одну из
своих возможных n
реакций.
Допустим, ЛПР выбрало i–е
действие и получило в ответ j-ю
реакцию. Совместными действиями ЛПР и
его противника порождается ситуация,
характеризуемая для ЛПР полезностью
.
Когда значение полезности отрицательно,
оно называется антиполезностью
или вредом.
Будем также полагать, что ЛПР не знает
определённо, какой ответ выберет
противник, но вероятности реакций
противника могут быть или известны, или
частично известны, или же эти вероятности
могут быть совсем неизвестны. Однако в
любом случае выполняется условие
Задача состоит в
том, чтобы выработать для ЛПР правила
отбора вариантов на основе анализа
матрицы
.
Правила отбора вариантов принято
называть критериями
принятия решений (КПР).
Классификация противников.
Противник, не стремящийся уменьшить выигрыш или увеличить проигрыш лица, принимающего решение, называется равнодушным противником. В роли равнодушного противника обычно выступает природа. Противника, который стремится уменьшить выгоду лица, принимающего решение, чтобы увеличить собственную, естественно называть конкурентом.
И наконец, враг – это тот, кто стремится не только уменьшить выгоду противника, но и увеличить его потери даже ценой собственных потерь.
Последовательное использование какого-либо определенного КПР или определенного набора КПР в серии принимаемых решений также называется стратегией, что не противоречит ранее данному определению
Итак, математическое представление задачи о принятии решения сводится к тому, что ЛПР выбирает строку в матрице полезности, которая представляет собой как бы меню из возможных ответов противника. После того как ЛПР выбрал строку, противник с какой-то вероятностью «преподносит» ему нечто из этого меню, но обязательно что-то одно, характеризуемое значением полезности .
Р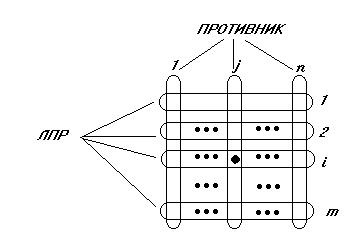
ис.1.
Вид матрицы принятия решений
На рис.1. столбцы соответствуют ответам противника, а строки - выбору ЛПР.
*Стратегия «пессимиста».
Человек, который не верит в свою удачу, последовательно, раз за разом, выбирает строку альтернатив – ответов противника, содержащую минимальный из всех возможных проигрышей. Он как бы говорит себе: «Все равно я проиграю, так пусть мой проигрыш будет как можно меньше».
*Стратегия «оптимиста».
Оптимист(авантюрист) безрассудно верит в свою удачу. Он последовательно, раз за разом выбирает строку, содержащую максимальный из возможных выигрышей, в надежде, что именно он-то ему и выпадет, и ему обязательно удастся «сорвать куш».
*Стратегия «реалиста».
Рационалист (реалист) отдает себе отчет в том, что он рискует, осуществляя выбор, и потому неизменно выбирает строку ответов противника, в которой максимально математическое ожидание выигрыша.
*"Внешняя" и "внутренняя" стратегии.
Внешняя с. – всё зависит от внешних обстоятельств (от судьбы не уйдешь).
Внутренняя с. – всё зависит от самого человека, его личных качеств( ч. сам кузнец своего счастья)