
- •Предисловие
- •Введение в теорию вероятностей События
- •Понятие вероятности
- •Аксиомы вероятности
- •Следствия из аксиом вероятности
- •Классический способ вычисления вероятностей
- •Геометрический способ вычисления вероятностей
- •Условная вероятность
- •Правило произведения
- •Формула полной вероятности
- •Формула гипотез (Байеса)
- •Независимость двух событий
- •Свойства независимых событий
- •Независимость трех и более событий
- •Последовательность независимых испытаний с двумя исходами
- •Локальная теорема Муавра Лапласа
- •Приближение Пуассона
- •Интегральная теорема Муавра Лапласа
- •Теория Вероятностей
- •Дискретные случайные величины
- •Функция распределения
- •Свойства функции распределения
- •Вырожденная случайная величина
- •Распределение Бернулли
- •Биномиальное распределение
- •Геометрическое распределение
- •Равномерно распределённая случайная величина
- •Непрерывные случайные величины
- •Нормально распределённая случайная величина
- •Плотность вероятности дискретной случайной величины
- •Смешанные случайные величины
- •Н езависимость двух случайных величин
- •Независимость трёх и более случайных величин
- •Математическое ожидание
- •Примеры нахождения математических ожиданий
- •Распределение Пуассона
- •Экспоненциальное распределение
- •Распределение Коши
Распределение Коши
Организуем любым доступным
способом равномерно распределённую на
промежутке (/2;/2)
случайную величину T.
Её функция распределения будет иметь
вид
![]() Числа
промежутка (/2;/2)
нанесём на полуокружность единичного
радиуса (см. рис. 28). Построим числовую
прямую, касающуюся полуокружности в
точке нуль, и имеющую точку касания
своим началом. После того, как в
эксперименте получится значение
случайной величины T,
проведём луч из центра через полученную
точку полуокружности до пересечения с
касательной. При этом образуется число
X, являющееся
значением новой случайной величины,
распределение которой называется
распределением Коши. Найдём её функцию
распределения F(x).
Числа
промежутка (/2;/2)
нанесём на полуокружность единичного
радиуса (см. рис. 28). Построим числовую
прямую, касающуюся полуокружности в
точке нуль, и имеющую точку касания
своим началом. После того, как в
эксперименте получится значение
случайной величины T,
проведём луч из центра через полученную
точку полуокружности до пересечения с
касательной. При этом образуется число
X, являющееся
значением новой случайной величины,
распределение которой называется
распределением Коши. Найдём её функцию
распределения F(x).
![]()
 .
Последний переход объясняется тем, что
.
Последний переход объясняется тем, что
![]() .
График функции распределения показан
на рисунке 29.
.
График функции распределения показан
на рисунке 29.
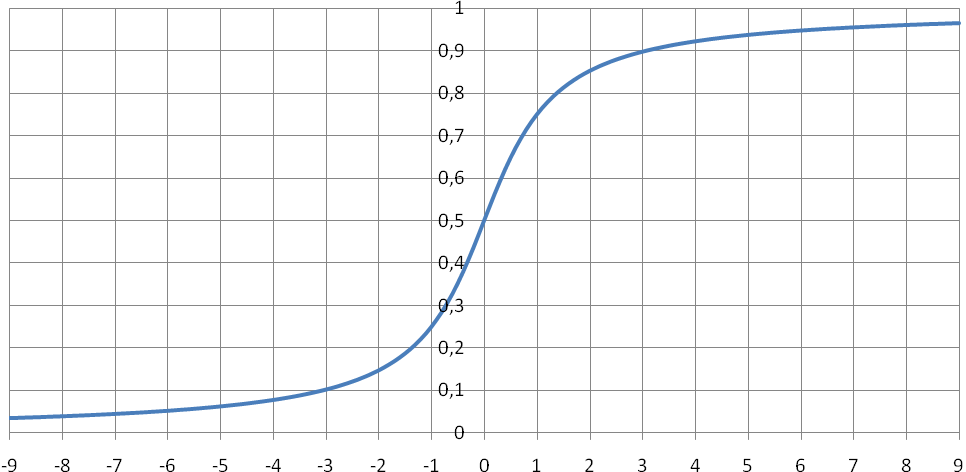
Рис. 29. Функция распределения случайной величины Коши.
Плотность вероятности
распределения Коши равна производной
от найденной функции распределения
![]() .
Убедимся в выполнении условия нормировки:
.
Убедимся в выполнении условия нормировки:
![]()
![]() .
График плотности вероятности
показан на рисунке 30.
.
График плотности вероятности
показан на рисунке 30.
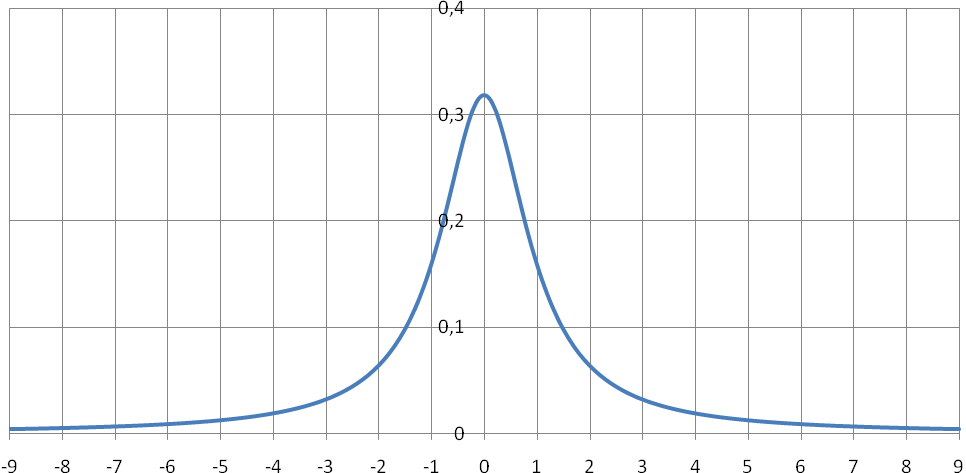
Рис. 30. Плотность вероятности распределения Коши.
Докажем, что у распределения Коши нет математического ожидания, для чего убедимся в расходимости несобственного интеграла:
![]() .
Сделаем замену переменных: t=1+x2dt=2x∙dx,
тогда если x=0, то t=1,
а если x+,
то t+,
поэтому
.
Сделаем замену переменных: t=1+x2dt=2x∙dx,
тогда если x=0, то t=1,
а если x+,
то t+,
поэтому
![]() .
Несобственный интеграл расходится,
поэтому математического ожидания
распределения Коши не существует, хотя
графики функции распределения и плотности
вероятности качественно напоминают
соответствующие графики для нормального
распределения. У графика плотности
вероятности так же есть перегибы
.
Несобственный интеграл расходится,
поэтому математического ожидания
распределения Коши не существует, хотя
графики функции распределения и плотности
вероятности качественно напоминают
соответствующие графики для нормального
распределения. У графика плотности
вероятности так же есть перегибы
![]() .
Только эти функции значительно медленнее
стремятся к своим пределам на бесконечности.
.
Только эти функции значительно медленнее
стремятся к своим пределам на бесконечности.
